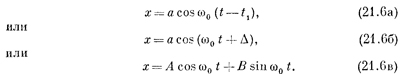| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Гармонический осциллятор
Для простоты предположим, что вышло так (или мы нужным образом изменили систему единиц), k/m = 1. Нам предстоит решить уравнение
После этого мы вернемся к уравнению (21.2), в котором kи m содержатся явно. Мы уже сталкивались с уравнением (21.3), когда только начинали изучать механику. Мы решили его численно [см. вып. 1, уравнение (9.12)], чтобы найти движение. Численным интегрированием мы нашли кривую (см. фиг. 9.4, вып. 1), которая показывает, что если частица m в начальный момент выведена из равновесия, но покоится, то она возвращается к положению равновесия. Мы не следили за частицей после того, как она достигла положения равновесия, но ясно, что она на этом не остановится, а будет колебаться (осциллировать). При численном интегрировании мы нашли время возврата в точку равновесия: t=1,570. Продолжительность полного цикла в четыре раза больше: t0~6,28 «сек». Все это мы нашли численным интегрированием, потому что лучше решать не умели. Но математики дали в наше распоряжение некую функцию, которая, если ее продифференцировать дважды, переходит в себя, умножившись на — 1. (Можно, конечно, заняться прямым вычислением таких функций, но это много труднее, чем просто узнать ответ.) Эта функция есть: x=cost. Продифференцируем ее: dx/dt = — sin t, a d2x/dt2 =—cos t = х. В начальный момент t=0, х=1, а начальная скорость равна нулю; это как раз те предположения, которые мы делали при численном интегрировании. Теперь, зная, что x = cost, найдем точное значение времени, при котором х=0. Ответ: t=π/2, или 1,57108. Мы ошиблись раньше в последнем знаке, потому что численное интегрирование было приближенным, но ошибка очень мала! Чтобы продвинуться дальше, вернемся к системе единиц, где время измеряется в настоящих секундах. Что будет решением в этом случае? Может быть, мы учтем постоянные k и m, умножив на соответствующий множитель cos t? Попробуем. Пусть x=A cos t, тогда dx/dt = —A sin t и d2t/dt2 = —Acost =—х. К нашему огорчению, мы не преуспели в решении уравнения (21.2), а снова вернулись - (21.3). Зато мы открыли важнейшее свойство линейных дифференциальных уравнений: если умножить решение уравнених>;на постоянную, то мы снова получим решение. Математически ясно — почему. Если х есть решение уравнения, то после умножения обеих частей уравнения на А производные тоже умножатся на А и поэтому Ах так же хорошо удовлетворит уравнению, как и х. Послушаем, что скажет по этому поводу физик. Если грузик растянет пружинку вдвое больше прежнего, то вдвое возрастет сила, вдвое возрастет ускорение, в два раза больше прежней будет приобретенная скорость и за то же самое время грузик пройдет вдвое большее расстояние. Но это вдвое большее расстояние — как раз то самое расстояние, которое надо пройти грузику до положения равновесия. Таким образом, чтобы достичь равновесия, требуется столько же времени и оно не зависит от начального смещения. Иначе говоря, если движение описывается линейным уравнением, то независимо от «силы» оно будет развиваться во времени одинаковым образом. Ошибка пошла нам на пользу — мы узнали, что, умножив решение на постоянную, мы получим решение прежнего уравнения. После нескольких проб и ошибок можно прийти к мысли, что вместо манипуляций с х надо изменить шкалу времени. Иначе говоря, уравнение (21.2) должно иметь решение вида
(Здесь ω0 — вовсе не угловая скорость вращающегося тела, но нам не хватит всех алфавитов, если каждую величину обозначать особой буквой.) Мы снабдили здесь ω индексом 0, потому что нам предстоит встретить еще много всяких омег: запомним, что ω0 соответствует естественному движению осциллятора. Попытка использовать (21.4) в качестве решения более успешна, потому что dx/dt =— ω0sinω0t и d2x/dt2 =—ω20cos ω0t = ω20х. Наконец-то мы решили то уравнение, которое и хотели решить. Это уравнение совпадает с (21.2), если ω20=k/m. Теперь нужно понять физический смысл ω0. Мы знаем, что косинус «повторяется» после того, как угол изменится на 2π. Поэтому x = cos ω0t будет периодическим движением; полный цикл этого движения соответствует изменению «угла» на 2π. Величину ω0t часто называют фазой движения. Чтобы изменить ω0t на 2π, нужно изменить t на t0 (период полного колебания); конечно, t0 находится из уравнения ω0t0=2π. Это значит, что ω0t0 нужно вычислять для одного цикла, и все будет повторяться, если увеличить t на t0; в этом случае мы увеличим фазу на 2π. Таким образом,
Значит, чем тяжелее грузик, тем медленнее пружинка будет колебаться взад и вперед. Инерция в этом случае будет больше, и если сила не изменится, то ей понадобится большее время для разгона и торможения груза. Если же взять пружинку пожестче, то движение должно происходить быстрее; и в самом деле, период уменьшается с увеличением жесткости пружины. Заметим теперь, что период колебаний массы на пружинке не зависит от того, как колебания начинаются. Для пружинки как будто безразлично, насколько мы ее растянем. Уравнение движения (21.2) определяет период колебаний, но ничего не говорит об амплитуде колебания. Амплитуду колебания, конечно, определить можно, и мы сейчас займемся этим, но для этого надо задать начальные условия. Дело в том, что мы еще не нашли самого общего решения уравнения (21.2). Имеется несколько видов решений. Решение x = cos ω0t соответствует случаю, когда в начальный момент пружинка растянута, а скорость ее равна нулю. Можно иначе заставить пружинку двигаться, например улучить момент, когда уравновешенная пружинка покоится (х = 0), и резко ударить по грузику; это будет означать, что в момент t=0 пружинке сообщена какая-то скорость. Такому движению будет соответствовать другое решение (21.2) — косинус нужно заменить на синус. Бросим в косинус еще один камень: если x = cos ω0t —решение, то, войдя в комнату, где качается пружинка, в тот момент (назовем его «t = 0»), когда грузик проходит через положение равновесия (х=0), мы будем вынуждены заменить это решение другим. Следовательно, x = cos ω0t не может быть общим решением; общее решение должно допускать, так сказать, перемещение начала отсчета времени. Таким свойством обладает, например, решение x = a cos ω0(t-t1), где t1 — какая-то постоянная. Далее, можно разложить
Некоторые из встречающихся в (21.6) величин имеют названия: ω0 называют угловой частотой; это число радианов, на которое фаза изменяется за 1 сек. Она определяется дифференциальным уравнением. Другие величины уравнением не определяются, а зависят от начальных условий. Постоянная а служит мерой максимального отклонения груза и называется амплитудой колебания. Постоянную Δ иногда называют фазой колебания, но здесь возможны недоразумения, потому что другие называют фазой ω0t + Δ и говорят, что фаза зависит от времени. Можно сказать, что Δ — это сдвиг фазы по сравнению с некоторой, принимаемой за нуль. Не будем спорить о словах. Разным Δ соответствуют движения с разными фазами. Вот это верно, а называть ли Δ фазой или нет — уже другой вопрос. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

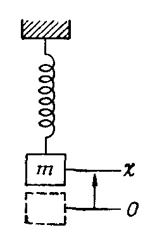 Пожалуй, простейшей механической системой, движение которой описывается линейным дифференциальным уравнением с постоянными коэффициентами, является масса на пружинке. После того как к пружинке подвесят грузик, она немного растянется, чтобы уравновесить силу тяжести. Проследим теперь за вертикальными отклонениями массы от положения равновесия (фиг. 21.1). Отклонения вверх от положения равновесия мы обозначим через х и предположим, что имеем дело с абсолютно упругой пружиной. В этом случае противодействующие растяжению силы прямо пропорциональны растяжению. Это означает, что сила равна —kх (знак минус напоминает нам, что сила противодействует смещениям). Таким образом, умноженное на массу ускорение должно быть равно —kх
Пожалуй, простейшей механической системой, движение которой описывается линейным дифференциальным уравнением с постоянными коэффициентами, является масса на пружинке. После того как к пружинке подвесят грузик, она немного растянется, чтобы уравновесить силу тяжести. Проследим теперь за вертикальными отклонениями массы от положения равновесия (фиг. 21.1). Отклонения вверх от положения равновесия мы обозначим через х и предположим, что имеем дело с абсолютно упругой пружиной. В этом случае противодействующие растяжению силы прямо пропорциональны растяжению. Это означает, что сила равна —kх (знак минус напоминает нам, что сила противодействует смещениям). Таким образом, умноженное на массу ускорение должно быть равно —kх