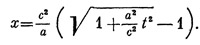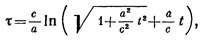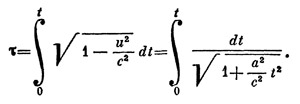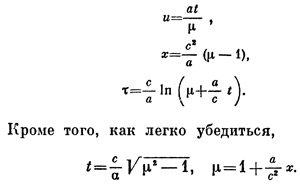Главная >> Введение в теорию относительности § 12. Равноускоренное движение
Простейшим видом неравномерного движения в классической механике является движение равноускоренное, при котором скорость тела растет пропорционально времени. По такому закону движется тело, находящееся под действием постоянной силы; примером может служить свободное падение вблизи земной поверхности или движение заряженной частицы в однородном электрическом поле.
Можно ли сформулировать подобный закон движения в теории относительности? Никто не мешает нам, конечно, и здесь назвать равноускоренным такое движение, при котором скорость меняется пропорционально времени. Однако мы тотчас сталкиваемся с тем затруднением, что движение, равноускоренное в одной системе отсчета, уже не будет таковым в другой системе. Кроме того, можно наверняка утверждать, что тело, находящееся под действием постоянной силы, не будет двигаться равноускоренно, ибо в противном случае оно в некоторый момент времени достигло бы скорости света, а затем стало бы двигаться еще быстрее, что совершенно невозможно.
Тем не менее, и в теории относительности можно рассмотреть движение, во многом аналогичное классическому равноускоренному движению и являющееся в некотором смысле простейшим неравномерным движением. Закон такого движения несколько сложнее, чем классический закон равноускоренного движения; чтобы ого сформулировать, мы рассмотрим следующий мысленный эксперимент.
Вообразим себе, например, ракету, снабженную достаточным запасом горючего и находящуюся где-нибудь в мировом пространстве, так что силы тяготения на нее практически не действуют. Пока двигатель ракеты не работает, она движется равномерно и прямолинейно; можно выбрать такую систему отсчета, в которой ракета будет неподвижна.
Когда же двигатель начнет работать, ракета будет двигаться ускоренно. Если при этом режим работы двигателя остается неизменным, то можно считать, что действующая на ракету сила будет постоянной. Правда, при этом будет обязательно уменьшаться масса ракеты — за счет отработанного горючего. Мы, однако, пренебрежем этим, считая, что расход топлива сравнительно мал. Спрашивается, по какому закону будет нарастать скорость ракеты?
Чтобы ответить на этот вопрос, мы сначала допустим, что двигатель работает не непрерывно, а «толчками», в промежутках же ракета движется по инерции. Предположим, что все эти толчки — одинаковой силы и следуют друг за другом через равные промежутки времени.
Скорость ракеты до первого толчка обозначим через u0; как уже было сказано, можно выбрать такую систему отсчета, в которой ракета вначале неподвижна. Тогда
uо = 0.
Эту систему отсчета обозначим через S. После первого толчка скорость ракеты возрастет на некоторую величину α, можно, стало быть, написать
u1 = α.
Какова же будет скорость после второго толчка? Очевидно, следует рассуждать так. После первого толчка ракета движется равномерно и прямолинейно. Возьмем новую систему отсчета S*, в которой она в это время неподвижна. Состояние ракеты в системе S* ничем не отличается от состояния в системе S до первого толчка. Так как, согласно предположению, режим работы двигателя остается постоянным, то после второго толчка ракета в системе S* получит такую же скорость а, какую она получила в системе S после первого толчка. Согласно закону сложения скоростей, скорость в системе S будет
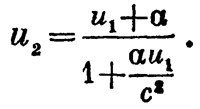 |
Теперь перейдем к системе отсчета S**, в которой ракета покоится после второго толчка; третий толчок сообщит ей в этой системе скорость α; переходя снова к основной системе S, получим
Этот процесс, очевидно, можно продолжать и дальше. Если скорость ракеты после n-го толчка в системе S есть un, то после (n+1)-го толчка она будет, очевидно, равна
Но это еще не все. Мы условились, что толчки следуют друг за другом через равные промежутки времени, но ничего не сказали о том, в какой системе отсчета нужно отмерять эти промежутки. После предыдущего рассуждения довольно ясно, что нужно каждый раз брать ту систему, в которой ракета между двумя последовательными толчками неподвижна. Если обозначить этот промежуток времени через β, то в системе отсчета S промежуток между двумя толчками будет равен
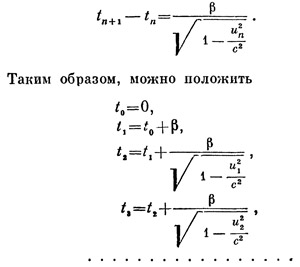 |
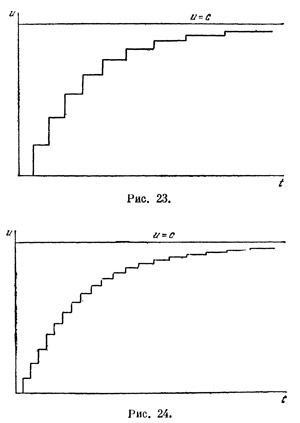
Таким образом, задавшись определенными значениями α и β, мы шаг за шагом можем вычислить одно за другим последовательные значения скорости и моменты толчков. Это толчкообразное нарастание скорости можно изобразить графически, если по горизонтальной оси откладывать время t, а по вертикальной — скорость и (рис. 23). Получится ступенчатая линия, причем, согласно закону сложения скоростей, высота ступенек постепенно убывает, а горизонтальная их длина, в соответствии с эффектом замедления времени, увеличивается. Линия наша ограничена сверху горизонтальной прямой, проведенной на уровне скорости света, к которой она неограниченно приближается.
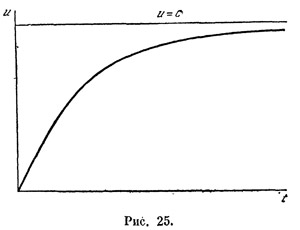
Если уменьшить силу каждого толчка, в то же время сделав их более частыми, так, чтобы отношение приращения скорости α к промежутку между толчками β осталось тем же самым, то новая ступенчатая линия будет иметь более мелкие ступеньки (рис. 24). Таким образом, мы можем строить все более и более мелкоступенчатые линии. В пределе мы получим уже гладкую кривую, отвечающую непрерывной работе двигателя
 |
(рис. 25). Уравнение ее можно получить методами интегрального исчисления. Оно, оказывается, имеет вид
где величина а равна отношению α/β, которое, согласно условию, в процессе предельного перехода оставалось постоянным. Его можно назвать собственным ускорением ракеты.
Приведем краткий вывод этого уравнения. Из написанного выше соотношения между un и un+1 имеем

Переменные разделены. После интегрирования будем иметь
Полагая постоянную интегрирования t0 равной нулю и разрешая полученное уравнение относительно u, приходим к указанной формуле. Нетрудно убедиться, что при t→∞ она дает и→с.
Пока произведение at мало по сравнению со скоростью света, знаменатель нашей формулы близок к единице и скорость нарастает почти пропорционально времени, т. е. по классическому закону. Но по мере роста скорости, и в особенности при приближении ее к скорости света, она нарастает все медленнее, за счет возрастания знаменателя. Об этом следовало бы помнить многим авторам научно-фантастических рассказов и романов, зачастую чересчур легко переносящих своих героев в «мир Эйнштейна».
 Какое же расстояние пролетает ракета, двигаясь по такому закону? Ответ на этот вопрос можно дать опять-таки только с помощью интегрального исчисления. Оказывается, что если ракета, как мы предполагали, в начале движения была неподвижна, то за время t (имеется в виду координатное время) она удалится от точки старта на расстояние Какое же расстояние пролетает ракета, двигаясь по такому закону? Ответ на этот вопрос можно дать опять-таки только с помощью интегрального исчисления. Оказывается, что если ракета, как мы предполагали, в начале движения была неподвижна, то за время t (имеется в виду координатное время) она удалится от точки старта на расстояние
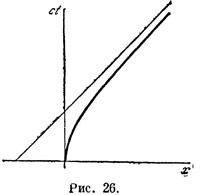
Это уравнение позволяет нам нанести мировую линию ракеты на плоскость событий. Оно является уравнением гиперболы (рис. 26), неограниченно приближающейся к световой линии. Ввиду этого такое движение часто называют гиперболическим; мы, однако, будем по-прежнему называть его равноускоренным движением, так как на это название никакое другое движение претендовать не может.
Для вывода этого уравнения нужно взять интеграл

Интересен также вопрос о собственном времени ракеты. Путем соответствующего интегрирования можно показать, что если часы в ракете и на Земле в момент старта показывают нуль, то в момент t координатного «земного» времени часы в ракете покажут время
где знаком In обозначен натуральный логарифм, т. е. логарифм при основании е=2,71828...
Формула эта получается интегрированием дифференциала собственного времени:
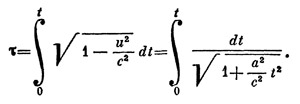 |
Результат можно выразить следующим образом через гиперболический синус:
a/c * t = sh a/c * τ
На этой «разнице времен» построены, как известно, сюжеты многих научно-фантастических рассказов и романов. Герой отправляется в космический рейс, летает с огромными скоростями год или два и возвращается на Землю, где за это время прошли десятки лет. Родные и близкие постарели или умерли. Потрясенный герой оплакивает их, а потом... потом все зависит от фантазии автора. Слов нет, иногда эти рассказы бывают довольно занимательны; жаль только, что нередко все впечатление портится из-за грубых ошибок авторов, зачастую весьма туманно представляющих себе вопрос о собственном времени и берущих различные цифры прямо с потолка. Чтобы составить себе представление об истинном положении вещей, попробуем рассчитать возможное движение ракеты и соответствующую разницу времен.
Одна из ближайших к Земле звезд —α Центавра — находится на расстоянии 4,28 светового года, что составляет 4,050 • 1013 км, ибо свет за год проходит 9,461 • 1012км. Допустим, что мы желаем полететь к этой звезде и вернуться обратно на Землю. Для экономии времени будем двигаться все время с ускорением (вопрос о технических возможностях такого полета мы оставляем в стороне). Чтобы не перегружать организм, ускорение космического корабля будем поддерживать равным ускорению силы тяжести на Земле, т. е. круглым счетом 10 м/сек2. Сколько времени будет продолжаться полет?
Весь путь можно разбить на четыре части: начальный разгон в течение первой половины пути, торможение до полной остановки, разгон в обратном направлении и торможение вплоть до спуска на Землю. Все условия движения на этих четырех этапах абсолютно тождественны, так что достаточно рассмотреть лишь одну четверть пути, учетверив затем результаты.
Если мы обозначим величину √(1 + a2/c2 * t2) через μ, то формулы для скорости, расстояния и собственного времени при равноускоренном движении принимают вид
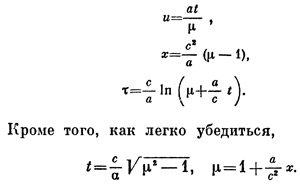
В течение четверти пути ракета покрывает расстояние в 2,025*1013 км. Так как а=0,01 км/сек2, то — a/c2*x = 2,250 и μ=3,250. Отсюда, как нетрудно подсчитать, t=9,277*107 сек, что составляет примерно 2 года 11 месяцев. Это — координатное, земное время. Таким образом, весь путь туда и обратно займет с точки зрения жителей Земли около 11 лет 9 месяцев.
Мы имеем, далее, a/c*t = 3,092, μ + a/c*t = 6,342. Взяв таблицу натуральных логарифмов, найдем, что In (μ + a/c*t) = 1,847, а так как (с/а)=3*107, то τ = 5,542*107 сек, т. е. примерно 1 год 9 месяцев. Это — уже собственное время путешественника. Таким образом, для него все путешествие займет около 7 лет, и он выиграет во времени против жителей Земли 4 года 9 месяцев. Разница довольно заметная, хотя, пожалуй, и не способная поразить воображение настолько, насколько этого желали бы многие авторы.
Интересно, что в один конец ракета по своему собственному времени будет лететь 3,51 года, тогда как свет, как мы указали с самого начала, тратит на тот же путь 4,28 года. В то же время ракета движется, конечно, всегда медленнее света. Читатель понимает, конечно, что тут нет никакого противоречия — мы сравниваем два различных времени, собственное и координатное. Кстати, максимальную скорость ракеты легко подсчитать — она составляет 2,854*105 км/сек, или 0,9513 скорости света.
При желании читатель может теперь рассчитать и другие космические маршруты. Участки, где ракета движется по инерции, затруднений, конечно, не представляют. Нелишне подчеркнуть, что все наши формулы относятся лишь к прямолинейному движению.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




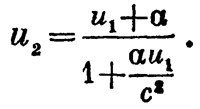
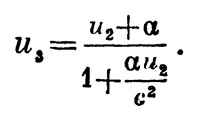
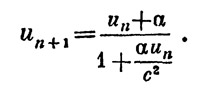


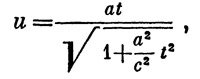

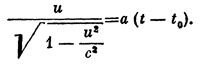
 Какое же расстояние пролетает ракета, двигаясь по такому закону? Ответ на этот вопрос можно дать опять-таки только с помощью интегрального исчисления. Оказывается, что если ракета, как мы предполагали, в начале движения была неподвижна, то за время t (имеется в виду координатное время) она удалится от точки старта на расстояние
Какое же расстояние пролетает ракета, двигаясь по такому закону? Ответ на этот вопрос можно дать опять-таки только с помощью интегрального исчисления. Оказывается, что если ракета, как мы предполагали, в начале движения была неподвижна, то за время t (имеется в виду координатное время) она удалится от точки старта на расстояние