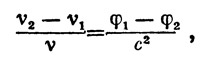Главная >> Введение в теорию относительности § 18. Собственное время в поле тяготения
В общей теории относительности все свойства поля тяготения полностью определяются формулой собственного времени. Зная, как выражается интервал собственного времени через координаты событий в любой точке поля, мы тем самым знаем и само поле. Это значит, что имея в руках формулу собственного времени, мы можем решить в принципе любую задачу, относящуюся к движению тел, распространению световых сигналов, и т. д. При этом с помощью принципа эквивалентности любой физический закон, полученный в рамках специальной теории относительности, мы можем сформулировать и для любого поля тяготения.
Рассмотрим с этой точки зрения закон инерции. Чтобы перенести его в общую теорию относительности, нужно иметь такую его формулировку, которая имеет силу в любых, инерциальных и неинерциальных, системах отсчета. Такую формулировку мы знаем: для тела, движущегося по инерции, интервал собственного времени принимает наибольшее значение. Что же означает такой закон в поле тяготения?
Пусть сначала поле тяготения отсутствует, но система отсчета неинерциальна. В такой системе тело, движущееся по инерции, движется неравномерно. С точки зрения того фиктивного поля тяготения, которое создается в этой системе силами инерции, движение по инерции означает не что иное, как свободное падение. Именно для свободно падающих тел интервал собственного времени будет максимальным.
Перейдем теперь к подлинному полю тяготения. Выделим в нем произвольный, но малый пространственный объем и выберем местную инерциальную систему отсчета. Здесь интервал собственного времени будет максимальным для тех тел, которые движутся равномерно и прямолинейно. Но в системе отсчета, связанной с тяготеющим телом, это — свободно падающие тела. Таким образом, вместо закона инерции в поле тяготения мы получаем следующий закон: интервал собственного времени принимает наибольшее значение для тел, которые в этом поле свободно падают.
Подбросим какое-нибудь тело вверх таким образом, чтобы оно после некоторого свободного полета упало обратно в ту же самую точку. Если мы сравним промежуток собственного времени этого тела с собственным временем тела, неподвижно лежащего на земной поверхности, то обнаружим, что для брошенного тела он будет больше, чем для неподвижного. При этом, правда, мы отбрасываем время, в течение которого тело ускоряется в начале полета и тормозится в конце; можно для большей наглядности вообразить, что его бросают у подножья башни, на вершине которой находится тело сравнения. Сравнивать показания часов у обоих тел следует в те моменты, когда брошенное тело пролетает мимо вершины башни.
Если мы вспомним расчет времени космического полета, произведенный нами в § 12, то обнаружим, что там результат получался обратный: для ускоренно двигавшейся ракеты промежуток собственного времени оказывался меньше, чем для неподвижных земных жителей. Конечно, здесь нет никакого противоречия, так как тогда мы не принимали во внимание никаких полей тяготения. Это было вполне законно, ибо ракета находилась в этих полях лишь в течение очень короткого по сравнению с продолжительностью всего полета времени.
В поле тяготения свободное падение эквивалентно движению по инерции, эквивалентно в том же смысле, в каком силы тяготения эквивалентны силам инерции. Свободное падение есть в этом смысле наиболее «естественное» состояние движения тела, так же как в отсутствие тяготения «естественным» является равномерное прямолинейное движение. Всякому изменению такого движения тело «сопротивляется»; при этом и возникают силы. С этой точки зрения вес тела есть не что иное, как его реакция на попытку удержать его от свободного падения. Нетрудно видеть, что это рассуждение представляет собой лишь перефразировку закона равенства инертной и тяжелой массы.
Итак, в поле тяготения собственное время для неподвижного тела течет, в некотором смысле, медленнее, чем для свободно падающего. Легко понять, что это замедление времени будет тем значительнее, чем сильнее поле. Например, на поверхности Солнца, где сила тяжести очень велика, время течет медленнее, чем на поверхности Земли; на Земле медленнее, чем на Луне, и т. д. Этому несколько неопределенному утверждению можно придать совершенно точный смысл.
Рассмотрим стационарное поле тяготения, т. е. поле, которое не меняется со временем. Имеется в виду, конечно, координатное время, ибо только оно может относиться ко всему полю в целом. Формула собственного времени дает его выражение через координаты событий; в частности, для неподвижных тел эта формула дает отношение собственного времени к координатному. В различных точках поля это отношение различно; при этом чем сильнее поле, тем больше отличается собственное время от координатного.
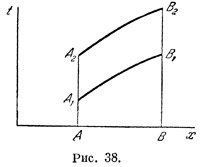 Пусть имеется два неподвижных тела, одно в точке, где поле сильно, другое — где оно слабо. Пусть первое тело А излучает световой сигнал, который принимается вторым телом В. Зная формулу собственного времени, мы можем найти полностью мировую линию сигнала— для этого можно воспользоваться тем, что вдоль такой линии интервал собственного времени обращается в нуль. Пусть это будет линия А1В1 (рис. 38; как всегда, изображена лишь одна пространственная координата). Пусть то же самое тело А излучает второй сигнал с мировой линией А2В2. Так как поле тяготения стационарного мировая линия второго сигнала полностью подобна первой, чтобы получить ее, достаточно просто сдвинуть вверх первую линию. Это значит, что через любую точку пространства оба сигнала пройдут через один и тот же промежуток координатного времени. Пусть имеется два неподвижных тела, одно в точке, где поле сильно, другое — где оно слабо. Пусть первое тело А излучает световой сигнал, который принимается вторым телом В. Зная формулу собственного времени, мы можем найти полностью мировую линию сигнала— для этого можно воспользоваться тем, что вдоль такой линии интервал собственного времени обращается в нуль. Пусть это будет линия А1В1 (рис. 38; как всегда, изображена лишь одна пространственная координата). Пусть то же самое тело А излучает второй сигнал с мировой линией А2В2. Так как поле тяготения стационарного мировая линия второго сигнала полностью подобна первой, чтобы получить ее, достаточно просто сдвинуть вверх первую линию. Это значит, что через любую точку пространства оба сигнала пройдут через один и тот же промежуток координатного времени.
Пусть первое тело излучает сигналы, например, через 1 секунду по своему собственному времени. Так как отношение собственного времени к координатному для тел А и В различно, то тело В будет принимать сигналы по своему собственному времени не через 1 секунду, а через другой промежуток времени; при этом разница полностью определяется разницей напряженности поля тяготения в точках А и В. Если в точке А поле сильнее, чем в В, то сигналы будут приняты через большие промежутки времени, и наоборот.
Мы уже знаем, что атомы излучают колебания сообразно своему собственному времени. Поэтому, если мы сравним спектры двух атомов водорода, один из которых находится на Солнце, а другой — на Земле, то, поскольку поле тяготения на Солнце сильнее, то и колебания от «солнечного» атома будут восприняты одним и тем же прибором как более медленные, чем колебания «земного» атома. Исследуя эти излучения под спектроскопом, мы обнаружим, что линии «солнечного» спектра сдвинуты по сравнению с «земным» к красному концу. Этот эффект получил название гравитационного красного смещения.
Все поля тяготения, с которыми приходится иметь дело в астрономии, являются с точки зрения теории относительности полями слабыми. Они достаточно полно характеризуются потенциалом тяготения φ, который для тел шарообразной формы имеет выражение
φ = - μm/r
Здесь m— масса тела, r— расстояние от центра, μ— постоянная тяготения, равная в системе CGS 6,670*10-8. Можно доказать, что если v1 и v2 — частоты одного и того же сигнала, измеренные в единицах собственного времени в точках с потенциалами φ1 и φ2, смещение этих частот выражается формулой
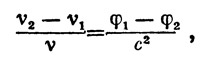 |
где под v можно понимать v1 или v2; в слабом поле эти две частоты весьма близки.
На поверхности Солнца r=6,963*1010 см, m=1,991*1033 г. Отсюда (φ/с2)——2,12*10-6.Для поверхности Земли имеем соответственно r=6,37*108см, m=5,98*1027г; поэтому на земной поверхности(φ/с2)——7*10-10. Кроме того, на земной орбите существует и потенциал, создаваемый солнечным тяготением; легко вычислить (радиус земной орбиты равен 1,5*1018 см), что этот потенциал равен —2*10-8. Поэтому при вычислении смещения частот потенциалом тяготения на поверхности Земли можно спокойно пренебречь — оп по крайней мере в сто раз меньше потенциала на поверхности Солнца. Отсюда получаем, что отношение смещения частоты к самой частоте будет равно — 2,12*10-6. Знак минус указывает на уменьшение частоты.
Экспериментальная проверка этого следствия общей теории относительности затрудняется сложностью физических условий, имеющих место на поверхности Солнца. Излучающие свет атомы на Солнце находятся в непрерывном и весьма интенсивном движении, которое вызывает смещение линий в силу эффекта Доплера и значительный их «размыв». Сильные электромагнитные поля, давление в солнечной атмосфере — все это в очень заметной степени влияет на спектральные линии. С другой стороны, все эти факторы сравнительно хорошо изучены и могут быть учтены; кроме того, приборы для исследования солнечного спектра обладают высокой степенью точности, что очень важно ввиду чрезвычайной малости гравитационного красного смещения. В результате длинного ряда исследований выяснилось, что эффект этот существует. Что касается его величины, то о точном согласии с теорией сказать что-либо с полной уверенностью пока еще трудно. Измерения но опровергают вывода теории относительности, но и полного подтверждения ее не дают. Все же по сравнению с искривлением световых лучей здесь теория с опытом согласуется, пожалуй, несколько лучше.
Гравитационное красное смещение должно наблюдаться также и в спектрах многих звезд. Большей частью, однако, это явление обнаружить невозможно по той простой причине, что неизвестна точная величина скорости звезды, а потому красное смещение нельзя отделить от обычного эффекта Доплера. Но здесь имеются некоторые счастливые исключения. Они относятся к двойным звездам; типичным примером является самая яркая звезда нашего неба — Сириус. Уже давно было обнаружено, что Сириус движется среди других звезд по странной извилистой линии. Было высказано предположение, что у него есть неяркий спутник с довольно большой массой. Обе эти звезды вращаются вокруг общего центра тяжести, поэтому и путь Сириуса имеет такой необычайный вид. Вскоре спутник Сириуса был обнаружен; яркость его, действительно, очень мала. Но его масса должна быть довольно значительной. Исследование этого вопроса привело к заключению, что масса спутника Сириуса близка к массе Солнца. С другой стороны, пришлось сделать вывод о том, что размеры его чрезвычайно малы — его диаметр лишь в три раза больше земного. Отсюда получается, что плотность вещества этого спутника поистине колоссальна — в 30 000 раз больше плотности воды! Сначала астрономы не хотели себе верить, но в дальнейшем развитие атомной физики показало, что этот факт не так удивителен и такая плотность вполне возможна. В настоящее время известно много таких звезд; они получили название белых карликов.
Но это значит, что напряжение силы тяжести на поверхности спутника Сириуса должно быть огромным — почти в 30 000 раз больше, чем на Земле. С другой стороны, движение этой звездной пары хорошо изучено, так что эффект Доплера мы уверенно можем отделить от других смещений спектральных линий.
Гравитационное красное смещение у спутника Сириуса установлено с полной несомненностью. К сожалению, мы плохо еще знаем его радиус; если все же использовать наилучшие имеющиеся данные, то согласив с теорией получается вполне удовлетворительное. Это же относится и к некоторым другим белым карликам.
Заметим, что одновременно с этим мы получаем весьма убедительное доказательство правильности заключения о чудовищной плотности этих звезд.
Важно отметить, что исследование гравитационного красного смещения доставляет нам сильное доказательство справедливости общего принципа эквивалентности. Излучение света атомами никак нельзя свести к чисто механическому движению; это — весьма сложный физический процесс. Поэтому одним законом равенства тяжелой и инертной массы в этом вопросе обойтись никак нельзя. Тот факт, что вывод теории относительности согласуется в данном случае с опытом, означает, что явление излучения света подчиняется принципу эквивалентности.
Весьма заманчивые перспективы в этом отношении открывает современная радиотехника. В силу ряда причин оптические методы исследования спектров имеют ограниченную точность, и предел здесь уже, можно сказать, достигнут. Иное дело — радиоволны. Здесь при сравнении частот можно добиться в миллион раз большей точности. Но тогда изменение частоты можно будет обнаружить уже в пределах Земли. Установив передатчик где-нибудь на вершине высокой горы, а приемник — в долине, можно будет заметить сдвиг частоты. Еще интереснее использовать для этой цели искусственные спутники Земли. Правда, необходимая точность пока еще не достигнута, но в самом ближайшем будущем следует ожидать новых интересных результатов.
В заключение вернемся еще раз к неоднократно обсуждавшемуся выше парадоксу часов. Если одни часы покоятся в некоторой инерциальной системе отсчета, а другие — описывают замкнутый путь, начинающийся и оканчивающийся близ первых часов, то по окончании движения оказывается, что вторые часы покажут меньший промежуток времени. Мы, конечно, как всегда, имеем в виду идеальные часы, являющиеся, по существу, синонимом собственного времени. Вторые часы движутся ускоренно; поэтому они на своем пути испытают действие сил инерции, эквивалентное действию сил тяготения. Эти силы и можно считать физической причиной замедления их хода. Если рассмотреть весь процессе системе отсчета, где вторые часы покоятся, то немедленно окажется, что первые часы «свободно падают». Согласия по закону, эквивалентному закону инерции, мы получаем, что первые часы должны показать больший промежуток собственного времени. На этом парадокс часов можно считать исчерпанным.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 Пусть имеется два неподвижных тела, одно в точке, где поле сильно, другое — где оно слабо. Пусть первое тело А излучает световой сигнал, который принимается вторым телом В. Зная формулу собственного времени, мы можем найти полностью мировую линию сигнала— для этого можно воспользоваться тем, что вдоль такой линии интервал собственного времени обращается в нуль. Пусть это будет линия А1В1 (рис. 38; как всегда, изображена лишь одна пространственная координата). Пусть то же самое тело А излучает второй сигнал с мировой линией А2В2. Так как поле тяготения стационарного мировая линия второго сигнала полностью подобна первой, чтобы получить ее, достаточно просто сдвинуть вверх первую линию. Это значит, что через любую точку пространства оба сигнала пройдут через один и тот же промежуток координатного времени.
Пусть имеется два неподвижных тела, одно в точке, где поле сильно, другое — где оно слабо. Пусть первое тело А излучает световой сигнал, который принимается вторым телом В. Зная формулу собственного времени, мы можем найти полностью мировую линию сигнала— для этого можно воспользоваться тем, что вдоль такой линии интервал собственного времени обращается в нуль. Пусть это будет линия А1В1 (рис. 38; как всегда, изображена лишь одна пространственная координата). Пусть то же самое тело А излучает второй сигнал с мировой линией А2В2. Так как поле тяготения стационарного мировая линия второго сигнала полностью подобна первой, чтобы получить ее, достаточно просто сдвинуть вверх первую линию. Это значит, что через любую точку пространства оба сигнала пройдут через один и тот же промежуток координатного времени.