Главная >> Введение в теорию относительности § 9. Геометрия пространства — времени
Пространственно-временные соотношения теории относительности допускают наглядное геометрическое истолкование, о котором мы и расскажем в настоящем параграфе. При этом мы ограничимся одномерным случаем, когда все рассматриваемые события располагаются вдоль одной и той же прямой. Как мы уже знаем, в этом случае для указания положения события в пространстве достаточно одной координаты, которую мы будем обозначать через х. Второй координатой будет, как всегда, время t.
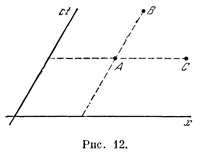 Прежде всего выберем (пока что) одну определенную систему отсчета, к которой и будем относить координаты всех событий. Затем возьмем лист бумаги и проведем на нем две пересекающиеся (не обязательно под прямым углом) прямые (рис. 12), одну из которых назовем пространственной осью, а другую временной. На каждой из осей в определенном масштабе будем откладывать соответствующие координаты событий. Всего удобнее единицы масштаба по обеим осям выбрать одинаковыми, но вдоль временной оси откладывать не время t, а величину ct. Тогда все особенности релятивистской кинематики выступят особенно выпукло. Прежде всего выберем (пока что) одну определенную систему отсчета, к которой и будем относить координаты всех событий. Затем возьмем лист бумаги и проведем на нем две пересекающиеся (не обязательно под прямым углом) прямые (рис. 12), одну из которых назовем пространственной осью, а другую временной. На каждой из осей в определенном масштабе будем откладывать соответствующие координаты событий. Всего удобнее единицы масштаба по обеим осям выбрать одинаковыми, но вдоль временной оси откладывать не время t, а величину ct. Тогда все особенности релятивистской кинематики выступят особенно выпукло.
Пусть дано некоторое событие А, координаты которого суть х и t. Отложив вдоль обеих осей соответствующие величины, проведем из полученных точек прямые, параллельные координатным осям. Точку пересечения этих прямых обозначим той же буквой А и назовем мировой точкой события А. Очевидно, каждому событию соответствует одна определенная мировая точка, при этом различным событиям соответствуют различные мировые точки.
Если два события происходят в одной и той же точке пространства, то их пространственные координаты совпадают. Поэтому их мировые точки на нашей «плоскости событий» будут лежать на прямой, параллельной временной оси (точки А и В на рис. 12). Если же два события происходят в один и тот же момент времени, то их мировые точки (А и С на том же рисунке) располагаются на прямой, параллельной пространственной оси. Из двух событий происходит позднее то, чья мировая точка больше удалена от пространственной оси.
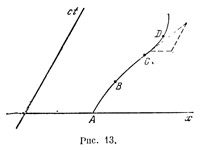 Рассмотрим теперь некоторое тело T размеры которого достаточно малы, т. е. так называемую материальную точку. Пребывание этого тела в данной точке пространства в данный момент времени можно рассматривать как некоторое событие; ему отвечает некоторая мировая точка. В следующий момент то же самое тело будет находиться, вообще говоря, в другой точке. Если мы нанесем на плоскость событий все соответствующие мировые точки, то получим линию — мировую линию тела Г. Такая линия дает, очевидно, полное представление о всей истории движения нашего тела. Так, рассматривая изображенную на рис. 13 мировую линию, мы заключаем, что материальная точка двигалась сначала вправо, и притом со сравнительно небольшой скоростью (участок АВ), так как ее мировая линия по мере роста t идет вправо, и притом почти параллельно временной оси. Затем наклон ее к этой оси увеличивается (участок ВС), значит, наша точка движется быстрее, за тот же промежуток времени она сдвигается на большее расстояние. Потом скорость снова уменьшается, и точка на мгновение останавливается (точка D) — это тот момент, когда касательная к мировой линии направлена параллельно временной оси. После этого точка движется уже в обратную сторону. Рассмотрим теперь некоторое тело T размеры которого достаточно малы, т. е. так называемую материальную точку. Пребывание этого тела в данной точке пространства в данный момент времени можно рассматривать как некоторое событие; ему отвечает некоторая мировая точка. В следующий момент то же самое тело будет находиться, вообще говоря, в другой точке. Если мы нанесем на плоскость событий все соответствующие мировые точки, то получим линию — мировую линию тела Г. Такая линия дает, очевидно, полное представление о всей истории движения нашего тела. Так, рассматривая изображенную на рис. 13 мировую линию, мы заключаем, что материальная точка двигалась сначала вправо, и притом со сравнительно небольшой скоростью (участок АВ), так как ее мировая линия по мере роста t идет вправо, и притом почти параллельно временной оси. Затем наклон ее к этой оси увеличивается (участок ВС), значит, наша точка движется быстрее, за тот же промежуток времени она сдвигается на большее расстояние. Потом скорость снова уменьшается, и точка на мгновение останавливается (точка D) — это тот момент, когда касательная к мировой линии направлена параллельно временной оси. После этого точка движется уже в обратную сторону.
Нетрудно также оценить и величину скорости точки в любой момент времени. Для этого нужно, как показано на рис. 13 пунктиром, в данной точке мировой линии провести к ней касательную и построить треугольник, одной стороной которого является отрезок этой касательной, а две другие стороны параллельны координатным осям. Отношение длин этих последних сторон и даст скорость точки. Следует только учесть, что скорость получится в особых, световых единицах, т. е. в таких единицах, в которых скорость света равна единице.
Равномерному и прямолинейному движению отвечает прямая мировая линия. Движение светового сигнала изображается прямой, параллельной той или другой биссектрисе координатных углов, смотря по тому, в какую сторону — направо или налево — движется сигнал. Мировые линии световых сигналов мы будем называть световыми линиями. Из каждой мировой точки выходят две световые линии; при этом они, как легко видеть, взаимно перпендикулярны.
Рассмотрим некоторое событие А. Проведем из мировой точки этого события обе световые линии (линии аа и bb на рис. 14). Они разделят плоскость событий на четыре части, обозначенные на рисунке цифрами 1, 2, 3, 4. Пусть другое событие В таково, что его мировая точка расположена в части 1 плоскости. Отрезок прямой, соединяющий точки А и В, наклонен к временной оси под углом, меньшим угла наклона световой линии; поэтому какое-либо тело или «сигнал», мировая линия которого совпадает с отрезком АВ, будет двигаться с «дозволенной» скоростью, меньшей скорости света. Направление такой линии называется временноподобным. Очевидно, что мировая линия любого материального тела в любой точке должна иметь временноподобное направление. Отсюда вытекает также, что событие А может быть причиной события В. Точно так же любое событие D, расположенное в части 3 плоскости, может быть (но не обязательно, конечно, будет в действительности) причиной события А, Вообще, если две мировые точки можно соединить отрезком временноподобной линии, то соответствующие события могут находиться в причинной связи.
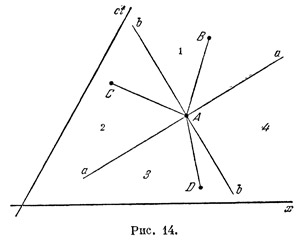 |
Иначе обстоит дело с событиями, расположенными в частях 2 и 4 плоскости. Никакой сигнал, движущийся не быстрее света, не может пройти, например, из А в С. Говорят, что отрезок АС имеет пространственноподобное направление. В этом случае ни одно из событий Л, С не может быть причиной другого.
Мы видим, таким образом, что простые геометрические соотношения между мировыми точками и линиями на плоскости событий дают нам довольно полное представление о характере движения тел, причинной связи событий и т. д. Оказывается, что столь же наглядно можно изобразить и переход от одной системы отсчета к другой, т. е. преобразования Лоренца.
Пусть даны две системы отсчета — система S и система S`, движущаяся относительно системы S со скоростью v. Выберем прежде всего оси координат и единицы масштаба для системы S. Теперь нам нужно на той же плоскости нанести координатные оси и определить единицы масштаба для системы S` таким образом, чтобы одно и то же событие изображалось в обеих системах отсчета одной и той же точкой A плоскости.
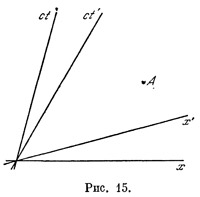 Для этого рассуждаем следующим образом. Точка, имеющая в системе отсчета S` пространственную координату х`, равную нулю, и покоящаяся в этой системе, в системе S движется со скоростью v. Если мы нанесем на нашу плоскость ее мировую линию, то получим некоторую временноподобную прямую (рис. 15). Но в системе S` эта точка покоится в начале координат, а потому ее мировая линия в этой системе должна просто совпадать с временной осью. Таким образом, временную ось для системы S` мы нашли. Для этого рассуждаем следующим образом. Точка, имеющая в системе отсчета S` пространственную координату х`, равную нулю, и покоящаяся в этой системе, в системе S движется со скоростью v. Если мы нанесем на нашу плоскость ее мировую линию, то получим некоторую временноподобную прямую (рис. 15). Но в системе S` эта точка покоится в начале координат, а потому ее мировая линия в этой системе должна просто совпадать с временной осью. Таким образом, временную ось для системы S` мы нашли.
Что же касается пространственной оси, то она состоит из всех тех мировых точек, которые отвечают событиям, происходящим в системе отсчета S` в момент времени t`=0. Из формул преобразований Лоренца вытекает, что между координатами этих событий в системе S должно выполняться соотношение ct - v/c*x = 0. Это — уравнение прямой. Нанеся ее на плоскость, замечаем, что, во-первых, она имеет пространственно-подобное направление. Можно показать, что она составляет с осью х такой же угол, какой с осью ct составляет только что найденная нами ось ct`. Это и будет пространственная ось для системы S`. Легко видеть, что биссектрисы координатных углов для обеих систем совпадают. Это значит, что световые линии в обеих системах координат будут одними и теми же; такова геометрическое выражение постоянства скорости света.
Выше мы убедились, что ответ на вопрос о том, могут ли быть два события причинно связаны друг с другом, целиком зависит от расположения их мировых точек относительно световых линий. Так как при изменении системы отсчета световые линии не меняются, то, следовательно, и причинная обусловленность явлений не зависит от выбора системы отсчета. Так, конечно, и должно быть.
Выше мы видели, что временная ось системы £" имеет на чертеже временноподобное направление, а пространственная ось — пространственноподобное (этим, между прочим, и объясняются названия этих направлений). Легко видеть, что верно и обратное. Если нам задано любое временноподобное направление, то, проведя через начало координат прямую, параллельную этому направлению, мы можем принять ее за временную ось новой системы координат. Пространственную ось проведем под таким же углом к старой пространственной оси. Точно так же, если задано любое пространственно-подобное направление, проведем новую пространственную ось параллельно этому направлению, выберем соответствующим образом новую временную ось и получим новую систему координат.
Если даны любые два события, мировые точки которых расположены так, что соединяющий их отрезок имеет временноподобное направление (как точки А и В на рис. 14), то всегда можно выбрать новую систему отсчета так, что эти два события будут происходить в одной и той же точке пространства. Для этого новую временную ось нужно направить параллельно отрезку АВ. Легко видеть также, что как бы мы ни проводили новую временную ось, событие В будет происходить после события A. Значит, если событие А является причиной события В, то в любой системе отсчета событие А наступает раньше, чем В.
Рассмотрим теперь на том же рис. 14 события A и С. Так как отрезок АС имеет пространственноподоб-ное направление, то можно выбрать новую систему координат так, что эти события будут происходить в один и тот же момент времени,— нужно новую пространственную ось взять параллельной отрезку АС.
 |
Наклоняя ее в ту или другую сторону, мы можем по своему произволу выбирать системы отсчета так, чтобы события А и С происходили в любом порядке! Таково геометрическое выражение факта относительности одновременности.
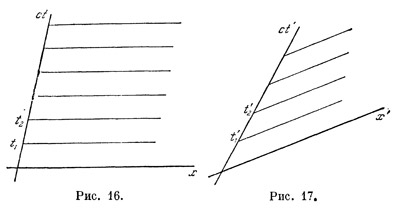
Выберем в системе отсчета S некоторый момент времени t1. События, происходящие в этот момент, заполнят на нашей плоскости (рис. 16) прямую, параллельную пространственной оси. Это будет как бы «моментальный снимок» со всего пространства, произведенный в момент t1. Взяв другой момент t2, получим другой «снимок», и т. д. Система отсчета как бы «расщепляет» единое пространство— время на отдельные «слои» — пространства в данные моменты времени.
Другая система отсчета S` производит такое расщепление несколько по-иному (рис. 17). «Моментальные снимки» пространства, произведенные в различных системах отсчета, будут отличаться. С этим обстоятельством тесно связаны многие «парадоксы» теории относительности.
Но мы пока что ничего не говорили о выборе единиц масштаба для различных систем отсчета. Для одной системы, например для S, единицы могут быть выбраны произвольно (но одинаковыми по обеим осям). Тогда единицы для любой другой системы S` выбираются следующим образом.
Мы видели, что при переходе к новой системе отсчета световые линии остаютстя неизменными. Оказывается,
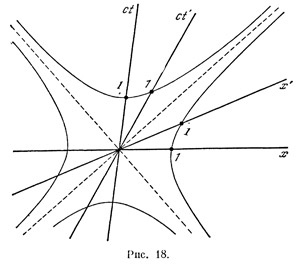 |
что аналогичным свойством обладают и некоторые другие линии. К числу их принадлежат линии, задаваемые уравнениями х2—c2t2 = 1 и х2—с2 t2= —1. В геометрии эти линии называются гиперболами; каждая из них состоит из двух «ветвей», так что мы получаем на плоскости четыре «куска» кривых, по одному в каждой части, на которые ее делят световые линии, выходящие из начала координат (пунктир на рис. 18). При удалении от начала координат эти кривые неограниченно приближаются к световым линиям, никогда, однако, их не пересекая.
 В любой системе отсчета S` эти гиперболы задаются теми же самыми уравнениями х`2—c2t`2 = 1и х`2—c2t`2 = — 1. Но из первого уравнения вытекает, t` = 0 будет х`2 = 1, т. е. x` = ±1. Это значит, что первая гипербола отсекает на оси х` по обе стороны от начала координат отрезки длиной 1 (в этой системе отсчета). Точно так же вторая гипербола отсекает единичные отрезки на временной оси. Таким образом, проведя эти гиперболы, мы тем самым определим единицы масштаба для любой системы отсчета. В любой системе отсчета S` эти гиперболы задаются теми же самыми уравнениями х`2—c2t`2 = 1и х`2—c2t`2 = — 1. Но из первого уравнения вытекает, t` = 0 будет х`2 = 1, т. е. x` = ±1. Это значит, что первая гипербола отсекает на оси х` по обе стороны от начала координат отрезки длиной 1 (в этой системе отсчета). Точно так же вторая гипербола отсекает единичные отрезки на временной оси. Таким образом, проведя эти гиперболы, мы тем самым определим единицы масштаба для любой системы отсчета.
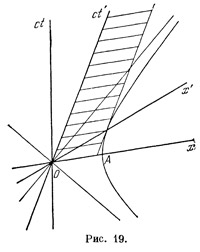
Теперь разобранные нами ранее релятивистские «эффекты» можно получить чисто геометрически. Вопрос об относительности одновременности мы уже разобрали. Рассмотрим лоренцово сокращение. Пусть некий твердый стержень покоится в системе отсчета S`. Это значит, что мировые линии его точек представляют собой прямые, параллельные временной оси системы S`. На рис. 19 проведены мировые линии концов стержня, причем для простоты длина его положена равной единице, а левый конец помещен в нулевую точку оси х` так что мировая линия этого конца совпадает с осью ct`. Чтобы измерить длину стержня в системе S, нужно, очевидно, измерить соответствующей единицей (отрезок ОА) масштаба отрезок, отсекаемый «мировой полосой» стержня на оси х (или любой прямой, ей параллельной). Из чертежа сразу видно, что эта длина будет меньше единицы.
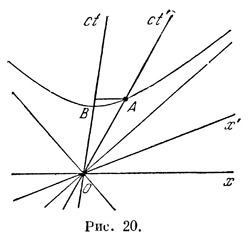 Столь же просто получается замедление времени. Пусть, например, события О и А происходят в одной и той же точке в системе S` (рис. 20). Опять-таки ради простоты положим, что их мировые точки лежат на оси ct`, а промежуток времени между ними равен единице. Разность временных координат этих событий в системе S мы получим, если проведем из точки А прямую, параллельную оси х, до пересечения с осью ct. Из чертежа ясно, что эта разность будет больше единицы. Столь же просто получается замедление времени. Пусть, например, события О и А происходят в одной и той же точке в системе S` (рис. 20). Опять-таки ради простоты положим, что их мировые точки лежат на оси ct`, а промежуток времени между ними равен единице. Разность временных координат этих событий в системе S мы получим, если проведем из точки А прямую, параллельную оси х, до пересечения с осью ct. Из чертежа ясно, что эта разность будет больше единицы.
Мы рекомендуем читателю с помощью этих графиков разобрать детально все наши «мысленные эксперименты», нанеся мировые линии концов и середины поезда, пути световых сигналов и т. д.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 Прежде всего выберем (пока что) одну определенную систему отсчета, к которой и будем относить координаты всех событий. Затем возьмем лист бумаги и проведем на нем две пересекающиеся (не обязательно под прямым углом) прямые (рис. 12), одну из которых назовем пространственной осью, а другую временной. На каждой из осей в определенном масштабе будем откладывать соответствующие координаты событий. Всего удобнее единицы масштаба по обеим осям выбрать одинаковыми, но вдоль временной оси откладывать не время t, а величину ct. Тогда все особенности релятивистской кинематики выступят особенно выпукло.
Прежде всего выберем (пока что) одну определенную систему отсчета, к которой и будем относить координаты всех событий. Затем возьмем лист бумаги и проведем на нем две пересекающиеся (не обязательно под прямым углом) прямые (рис. 12), одну из которых назовем пространственной осью, а другую временной. На каждой из осей в определенном масштабе будем откладывать соответствующие координаты событий. Всего удобнее единицы масштаба по обеим осям выбрать одинаковыми, но вдоль временной оси откладывать не время t, а величину ct. Тогда все особенности релятивистской кинематики выступят особенно выпукло. Рассмотрим теперь некоторое тело T размеры которого достаточно малы, т. е. так называемую материальную точку. Пребывание этого тела в данной точке пространства в данный момент времени можно рассматривать как некоторое событие; ему отвечает некоторая мировая точка. В следующий момент то же самое тело будет находиться, вообще говоря, в другой точке. Если мы нанесем на плоскость событий все соответствующие мировые точки, то получим линию — мировую линию тела Г. Такая линия дает, очевидно, полное представление о всей истории движения нашего тела. Так, рассматривая изображенную на рис. 13 мировую линию, мы заключаем, что материальная точка двигалась сначала вправо, и притом со сравнительно небольшой скоростью (участок АВ), так как ее мировая линия по мере роста t идет вправо, и притом почти параллельно временной оси. Затем наклон ее к этой оси увеличивается (участок ВС), значит, наша точка движется быстрее, за тот же промежуток времени она сдвигается на большее расстояние. Потом скорость снова уменьшается, и точка на мгновение останавливается (точка D) — это тот момент, когда касательная к мировой линии направлена параллельно временной оси. После этого точка движется уже в обратную сторону.
Рассмотрим теперь некоторое тело T размеры которого достаточно малы, т. е. так называемую материальную точку. Пребывание этого тела в данной точке пространства в данный момент времени можно рассматривать как некоторое событие; ему отвечает некоторая мировая точка. В следующий момент то же самое тело будет находиться, вообще говоря, в другой точке. Если мы нанесем на плоскость событий все соответствующие мировые точки, то получим линию — мировую линию тела Г. Такая линия дает, очевидно, полное представление о всей истории движения нашего тела. Так, рассматривая изображенную на рис. 13 мировую линию, мы заключаем, что материальная точка двигалась сначала вправо, и притом со сравнительно небольшой скоростью (участок АВ), так как ее мировая линия по мере роста t идет вправо, и притом почти параллельно временной оси. Затем наклон ее к этой оси увеличивается (участок ВС), значит, наша точка движется быстрее, за тот же промежуток времени она сдвигается на большее расстояние. Потом скорость снова уменьшается, и точка на мгновение останавливается (точка D) — это тот момент, когда касательная к мировой линии направлена параллельно временной оси. После этого точка движется уже в обратную сторону.
 Для этого рассуждаем следующим образом. Точка, имеющая в системе отсчета S` пространственную координату х`, равную нулю, и покоящаяся в этой системе, в системе S движется со скоростью v. Если мы нанесем на нашу плоскость ее мировую линию, то получим некоторую временноподобную прямую (рис. 15). Но в системе S` эта точка покоится в начале координат, а потому ее мировая линия в этой системе должна просто совпадать с временной осью. Таким образом, временную ось для системы S` мы нашли.
Для этого рассуждаем следующим образом. Точка, имеющая в системе отсчета S` пространственную координату х`, равную нулю, и покоящаяся в этой системе, в системе S движется со скоростью v. Если мы нанесем на нашу плоскость ее мировую линию, то получим некоторую временноподобную прямую (рис. 15). Но в системе S` эта точка покоится в начале координат, а потому ее мировая линия в этой системе должна просто совпадать с временной осью. Таким образом, временную ось для системы S` мы нашли.

 В любой системе отсчета S` эти гиперболы задаются теми же самыми уравнениями х`2—c2t`2 = 1и х`2—c2t`2 = — 1. Но из первого уравнения вытекает, t` = 0 будет х`2 = 1, т. е. x` = ±1. Это значит, что первая гипербола отсекает на оси х` по обе стороны от начала координат отрезки длиной 1 (в этой системе отсчета). Точно так же вторая гипербола отсекает единичные отрезки на временной оси. Таким образом, проведя эти гиперболы, мы тем самым определим единицы масштаба для любой системы отсчета.
В любой системе отсчета S` эти гиперболы задаются теми же самыми уравнениями х`2—c2t`2 = 1и х`2—c2t`2 = — 1. Но из первого уравнения вытекает, t` = 0 будет х`2 = 1, т. е. x` = ±1. Это значит, что первая гипербола отсекает на оси х` по обе стороны от начала координат отрезки длиной 1 (в этой системе отсчета). Точно так же вторая гипербола отсекает единичные отрезки на временной оси. Таким образом, проведя эти гиперболы, мы тем самым определим единицы масштаба для любой системы отсчета. Столь же просто получается замедление времени. Пусть, например, события О и А происходят в одной и той же точке в системе S` (рис. 20). Опять-таки ради простоты положим, что их мировые точки лежат на оси ct`, а промежуток времени между ними равен единице. Разность временных координат этих событий в системе S мы получим, если проведем из точки А прямую, параллельную оси х, до пересечения с осью ct. Из чертежа ясно, что эта разность будет больше единицы.
Столь же просто получается замедление времени. Пусть, например, события О и А происходят в одной и той же точке в системе S` (рис. 20). Опять-таки ради простоты положим, что их мировые точки лежат на оси ct`, а промежуток времени между ними равен единице. Разность временных координат этих событий в системе S мы получим, если проведем из точки А прямую, параллельную оси х, до пересечения с осью ct. Из чертежа ясно, что эта разность будет больше единицы.