Главная >> Введение в теорию относительности § 7. Замедление времени
Вернемся еще раз к нашему поезду. Допустим, что, например, в его заднем конце происходят два события,
моменты наступления которых пусть будут t`0 и t`1. На основании предыдущего опыта мы не можем ожидать, что и для неподвижного наблюдателя моменты этих событий будут теми же самыми; обозначим их поэтому теперь через t`0 и t`1. Нашей задачей будет сейчас найти соотношение, связывающее промежуток времени
t`1 — t`0 с промежутком t1 — t0.
Для этого предположим, что одновременно с первым событием из этой точки к переднему концу поезда отправляется световой сигнал, который отражается там от зеркала и возвращается обратно как раз в момент наступления второго события. Для этого едущий в поезде наблюдатель должен установить зеркало на расстоянии c*(t`1 — t`0)/2 от места, где происходят события.
Перейдем на точку зрения неподвижного наблюдателя. Для него поезд движется со скоростью v, а потому световой сигнал сначала догоняет зеркало, а потом летит навстречу той точке, из которой он был выпущен. Кроме того, расстояние между местом событий и зерка лом равно не c*(t`1 — t`0)/2, а в силу лоренцова сокращения величине

Останется подставить сюда величину 2а/с, которая, очевидно, равна (t`1—t`0) √(1 - v2/c2). Получаем окончательно
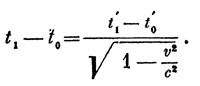 |
Следовательно, промежуток времени t1—t0 больше промежутка t`1—t`0. Это значит, что если, например, в поезде установлены часы, отбивающие секунды, то неподвижный наблюдатель найдет, что промежуток времени между двумя последовательными ударами больше секунды, т. е. с его точки зрения часы в поезде отстают.
Но, согласно принципу относительности, оба наблюдателя равноправны. Поэтому для наблюдателя в поезде отставать будут, наоборот, «земные» часы. Замедление времени так же «взаимно», как и лоренцово сокращение; и по-прежнему, конечно, в этом нет никакого противоречия. Для разных наблюдателей одни и те же процессы протекают по-разному; при этом все наблюдатели равноправны. Описание какого-нибудь явления, данное с одной точки зрения, мы всегда можем перевести на «язык» другой точки зрения. В следующем параграфе для этого будут даны полные формулы. В то же время бессмысленно пытаться совсем освободиться от какой бы то ни было «точки зрения», точно так же как пытаться изложить какую-нибудь мысль без всякого конкретного языка. Любое высказывание есть высказывание на каком-то определенном языке — русском, немецком, китайском, английском и т. д. Мы всегда имеем возможность перевода с одного языка на другой. Но нелепо требовать, чтобы это высказывание было передано «таким, каково оно есть», без всякого языка.
Однако в факте относительности времени заключен все же некий парадокс. Предположим сначала, что поезд стоит у станции. Тогда установленные в нем часы идут с той же скоростью, что и «земные». Пусть теперь поезд трогается. По мере того как он набирает скорость, неподвижный наблюдатель обнаруживает, что часы в поезде все больше отстают. Пусть, далее, пройдя некоторое расстояние, поезд тормозит, останавливается, а затем пускается в обратный путь, прибывает на ту же станцию и здесь останавливается окончательно. Все время, пока он двигался, его часы шли медленнее часов неподвижного наблюдателя. По окончании эксперимента окажется, следовательно, что часы в поезде отстали по сравнению с «земными», т. е. их стрелки сделали меньшее число оборотов.
Но ведь, согласно принципу относительности, мы имеем право считать поезд неподвижным, а землю —-движущейся! Только для наблюдателя в поезде все явления должны протекать в обратном порядке, и он должен прийти к выводу, что отстали, наоборот, «земные» часы.
Так какие же часы все-таки отстали? И не пришли ли мы к противоречию? Конечно, нет. Дело в том, что в наших рассуждениях содержится ошибка — мы не имеем права считать в данном случае обоих наблюдателей равноправными, так как поезд движется неравномерно. Принцип относительности распространяется лишь на равномерные и прямолинейные движения; физические законы для наблюдателя в поезде выглядят несколько иначе, чем для неподвижного наблюдателя. Это не значит, что на точку зрения движущегося наблюдателя в данном случае вообще нельзя становиться,— просто наши формулы к этому случаю не относятся; теперь нужны другие, более сложные формулы. Забегая вперед, скажем, что в действительности отстанут часы именно в поезде и по этому признаку можно безошибочно сказать, что он двигался неравномерно. Впрочем, к этому парадоксу часов мы еще будем иметь случай вернуться.
Интересно, что эффект замедления времени был, по существу, получен еще Лоренцом. Мы уже упоминали о том, что Лоренц установил для уравнения Максвелла некий особый принцип относительности. Принцип этот требовал, чтобы в системе движущихся сквозь эфир тел было введено новое время, отличающееся от «истинного». Лишь при этом условии уравнения Максвелла сохраняли свой вид, т. е. оставались в силе и для движущихся зарядов. Это местное, или эффективное, время Лоренц считал некоей математической фикцией, нужной лишь для упрощения выкладок; реальный физический смысл он признавал лишь за «истинным» временем. Но по мере развития теории все более ясно обнаруживалось, что физические процессы в движущейся системе тел подчиняются именно этому эффективному времени, а отнюдь не «истинному», которое все больше утрачивало реальный смысл. Оказалось, что это «истинное» время нельзя даже измерить, оно стало какой-то «тенью». Эйнштейну оставалось лишь окончательно выбросить эту «тень» из рассмотрения вместе с эфиром и прочими наслоениями. Можно сказать поэтому, что Лоренц сам выковал оружие против своей собственной теории. После появления работ Эйнштейна Лоренц с мужеством настоящего ученого признал его правоту и ошибочность собственных позиций.
Излишне говорить о том, что поиски динамических причин замедления времени так же бессмысленны, как и в случае лоренцова сокращения. Так же, как и там, это — одно из проявлений свойств пространства и времени. Заметим также, что наряду с рассматриваемым относительным временем в теории относительности существует и другое, абсолютное время. С ним мы познакомимся позднее.
Мы не будем сейчас заниматься вычислениями, долженствующими показать крайнюю малость замедления времени в обычных условиях. Читатель без труда проведет их сам, воспользовавшись той же приближенной формулой. Гораздо важнее, что этот эффект является одним из тех, которые с полной отчетливостью удалось обнаружить на опыте.
Для его обнаружения необходимы, конечно, огромные скорости; ясно поэтому, что обычные часы, вроде секундомеров, здесь совершенно непригодны. К счастью, здесь природа позаботилась сама, предоставив в наше распоряжение весьма точные часы, которым можно сообщать самые высокие скорости без опасения испортить механизм. Речь идет об «атомных часах».
Известно, что атомы всех элементов в определенных условиях испускают лучи света вполне определенных частот; совокупность этих частот характерна для данного элемента и составляет его спектр. Рассматривая излучение данного элемента через прибор для изучения спектров — спектроскоп, мы увидим ряд линий, каждая из которых отвечает одной из частот спектра.
Исследуя под спектроскопом излучение далеких звезд, астрономы обнаружили среди многочисленных линий их спектров те, которые совпадают с линиями уже известных на Земле элементов; ныне этот спектральный анализ является могущественнейшим орудием астрофизики. Но спектры многих звезд обнаруживают одну особенность — линии их спектров зачастую находятся не на положенных местах, а бывают слегка сдвинуты (все сразу) в ту или другую сторону. Таким образом, частоты всех световых колебаний, испускаемых звездой, оказываются несколько смещенными. Это явление объясняется движением звезд относительно Земли.
Пусть, например, звезда и Земля сближаются. Если стать на точку зрения неподвижной звезды, то окажется, что Земля встречает «гребни» световых волн чаще, чем если бы она была неподвижна; это и значит, что излучаемые звездой колебания воспринимаются на Земле с большей частотой. С точки зрения неподвижной Земли звезда как бы нагоняет свой собственный свет; поэтому длины световых волн укорачиваются, а более короткие волны отвечают более высокой частоте. Если звезда и Земля взаимно удаляются, то дело, очевидно, будет наоборот — частота уменьшится.
Этот эффект изменения частот давно известен; он называется эффектом Доплера. Как видим, объяснение его не требует привлечения теории относительности — он является эффектом классическим. Эффект Доплера служит одним из самых надежных средств измерения лучевых скоростей звезд, т. е. их скоростей вдоль луча зрения, соединяющего светило с Землей. Если звезда движется перпендикулярно к лучу зрения, эффект отсутствует. Читателю известно, конечно, что аналогичный эффект наблюдается и при распространении звуковых волн.
Теория относительности, сохраняя в основных чертах объяснение эффекта Доплера, вносит в него небольшую поправку. Каждый атом испускает световые колебания, сообразуясь со своим собственным временем. Если звезда относительно Земли движется, то все процессы там для земного наблюдателя несколько замедлены, и поэтому в дополнение к классическому должен наблюдаться также небольшой релятивистский эффект. Этот последний не зависит от направления скорости и определяется только ее абсолютной величиной. Даже если звезда движется точно перпендикулярно к лучу зрения, так что классический эффект отсутствует, релятивистский эффект должен наблюдаться.
Так как в нашем распоряжении нет способа достаточно точно контролировать направление и скорость движения звезд, отделить релятивистский эффект от классического в условиях астрономических наблюдений мы не в состоянии. Однако в лабораторных условиях такую возможность создать можно.
Современная электронная техника позволяет создавать потоки атомов и разгонять их до огромных скоростей, приближающихся к скорости света. Поставив спектроскоп сбоку, перпендикулярно к направлению движения атомов, можно надеяться обнаружить чисто релятивистский поперечный эффект Доплера. Трудность здесь состоит в том, чтобы отделить этот малый поперечный эффект от гораздо большего продольного классического эффекта, проявляющегося при малейшем отклонении положения спектроскопа от строго перпендикулярного направления. Трудности эти удалось преодолеть, и поперечный эффект Доплера был обнаружен и измерен. Результаты оказались прекрасно согласующимися с выводами теории относительности. Таким образом, относительность времени оказывается вполне реальным фактом, подтвержденным экспериментальным путем.
Другое подтверждение этот вывод теории относительности нашел при исследовании космических лучей. Проникая в земную атмосферу, эти лучи вызывают ливни «элементарных» частиц, среди которых встречаются мезоны с очень коротким временем «жизни», по прошествии которого они распадаются, превращаясь в другие частицы. Оказалось, что быстро движущиеся мезоны «живут» в 10—20 раз дольше, чем медленные. Здесь тоже проявляется релятивистский эффект замедления времени. Каждый мезон «сам для себя» существует в среднем одно и то же время (около 200 микросекунд). Но приборы регистрируют это время по-разному, в зависимости от скорости самого мезона относительно прибора. Предлагаем читателю на основании этих данных рассчитать скорости быстрых мезонов.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|