| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
5. Существует ли вообще движение?
Совершенно особую точку зрения по вопросу о движении имели древнегреческие философы, жившие в VI и V столетиях до н. э. на Апеннинском полуострове в городе Злее (их называют элеатами). Размышляя о движении тел, элеаты пришли к выводу, что движения вообще не существует. Если же мы и видим в природе движение, утверждали они, то это всего лишь обман чувств. Настолько ошибочны могут быть человеческие чувства! Особенно интересными были рассуждения о невозможности движения у элеата Зенона. Приведем здесь его четыре знаменитых апории?
Ахиллес и черепаха. Герой Троянской войны Ахиллес славился тем, что очень быстро бегал. Зенон, однако, доказывал, что Ахиллес не способен перегнать даже черепаху. Как это возможно? Пусть, понадеявшись на свои быстрые ноги, Ахиллес возьмет старт далеко позади черепахи. Черепаха начнет ползти от точки A1 Ахиллес же побежит от точки А, лежащей позади нее (рис. 8). К тому времени, как Ахиллес достигнет точки A1, черепаха переползет в точку A2. К моменту же, когда Ахиллес добежит до точки A2, черепаха будет уже в точке A3 и т. д. и т. д. Быстроногий Ахиллес никогда не догонит медлительной черепахи. Значит, движения не существует.
Стадии. Здесь Зенон показывает, что признание существования движения приводит к бессмысленному выводу: целое равняется своей половине. Пусть три ряда всадников будут расположены так, как показано на рис. 9. Длина всех трех рядов одинакова. Пусть второй ряд начинает двигаться налево, третий — направо. Через некоторое время всадники расположатся так, как показано на рис. 10. Последний всадник третьего ряда миновал половину первого ряда и весь второй ряд. Следовательно, целое равно своей половине. Этот бессмысленный вывод должен показывать, что движение действительно невозможно. Если расстояние между точками А и В равно а, то при движении со скоростью v это расстояние будет пройдено за а/v сек. Сложив все эти промежутки, получим время, затраченное на то, чтобы пройти путь АВ,
Апорию об Ахиллесе и черепахе приводит на страницах романа «Война и мир» Лев Толстой. Он пишет: «Для человеческого ума непонятна абсолютная непрерывность движения. Человеку становятся понятны законы какого бы то ни было движения только тогда, когда он рассматривает произвольно взятые единицы этого движения. Но вместе с тем из этого-то произвольного деления непрерывного движения на прерывные единицы проистекает большая часть человеческих заблуждений. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

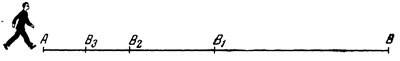 Рис. 7. По Зенону, путь конечной длины невозможно пройти за конечное время
Рис. 7. По Зенону, путь конечной длины невозможно пройти за конечное время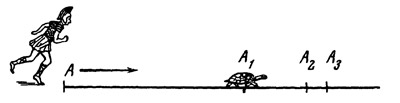 Рис. 8. Ахиллес и черепаха
Рис. 8. Ахиллес и черепаха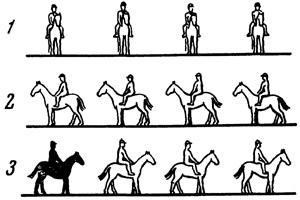 Рис. 9. По Зеноун, признание движения приводит к абсурду: целое равно своей половине
Рис. 9. По Зеноун, признание движения приводит к абсурду: целое равно своей половине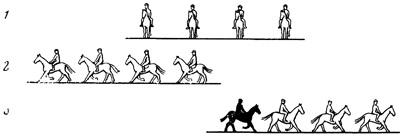 Рис. 10. Объяснение то же, что и к рис. 9
Рис. 10. Объяснение то же, что и к рис. 9