Главная >> В мире больших скоростей >> Специальная теория относительности 6. Какова скорость течения времени?
Увлекшись интересным делом или читая занимательную книгу, мы порою не замечаем, как летит время; когда же занимаемся скучным дедом, время тянется долго. Однако каждому ясно, что в этом повинно не действительное физическое время, а только наше субъективное ощущение времени. Как же обстоит дело с физическим временем, какова скорость его течения? Велика она или мала? Более тщательное рассмотрение показывает, что ответить на этот вопрос невозможно, точно так же как человеку, находящемуся в изолированном помещении, невозможно решить, верно ли идут его единственные часы. О ходе часов можно судить, сравнивая их с какими-нибудь другими часами. О скорости течения времени можно судить, лишь сравнивая его с течением какого-то другого времени.
Поставить вопрос о скорости течения времени можно, например, так: как велика скорость течения времени в соседней комнате по сравнению со скоростью течения времени в нашей комнате или как велика скорость течения времени на летящем реактивном самолете по сравнению со скоростью течения времени на аэродроме? На эти вопросы можно ответить, если, например, сравнить ход идеально точных часов на самолете с ходом таких же часов на аэродроме. Если такое сравнение произведет наблюдатель, находящийся на аэродроме, и найдет, что во время полета часы летчика отстают от часов на Земле, то он может сказать: «Время на самолете относительно земной поверхности течет медленнее, чем на земле».
Как видно, для решения вопроса о скорости течения времени прежде всего необходимы идеальные часы, т. е. такие часы, которые идеально точно отражают скорость течения времени — без погрешностей, обусловленных несовершенством механизма. В качестве часов пригоден всякий регулярный процесс природы, например распад радиоактивных веществ. Для каждого радиоактивного элемента характерен свой период полураспада, т. е. время, в течение которого число атомов вещества успевает уменьшиться наполовину. Период полураспада радия, например, составляет 1590 лет. За это время половина атомов радия превращается в атомы другого элемента — радона. Последние, в свою очередь, распадаются дальше. Для сравнения течения времени на самолете и на аэродроме представим себе, что на них помещено по кусочку радия (которые служат часами). Предположим, что к тому моменту, как самолет возвратится обратно, на аэродроме распалась одна миллионная часть радия. Если в тот же момент измерить количество радия, оставшегося на самолете, и если окажется, что на самолете тоже распалась одна миллионная часть радия, то это будет означать, что и на Земле, и на самолете время протекало одинаково. Если же число распавшихся атомов на самолете окажется меньше, то это покажет, что на самолете время протекало медленнее, чем на Земле.
Читатель сразу же заметит, что в приведенном примере для сравнения часов были созданы благоприятные условия: самолет в нужный момент вернулся на аэродром. Как же сравнить часы, если самолет, скажем, все время удаляется от аэродрома равномерно и прямолинейно? Чтобы ответить на этот вопрос, остановимся несколько подробнее на сравнении часов.
Если часы находятся «в одной и той же точке пространства» (практически это означает, что расстояние между часами ничтожно мало), то для их сравнения требуется только взглянуть на циферблаты. Луч света донесет изображения обоих часов до глаза, и мы увидим стрелки часов в том положении, в котором они находятся одновременно — как раз это и существенно при сравнении часов.
Если часы находятся на некотором конечном расстоянии друг от друга и неподвижны друг относительно друга, то в этом случае сравнить их несложно. Для этого наблюдатель должен расположиться на равных расстояниях от обоих часов. Так как лучи света от одних часов дойдут до наблюдателя за то же время, что и от других часов, то наблюдатель увидит стрелки часов в положениях, относящихся опять-таки к одному и тому же моменту времени. Существенно лишь, чтобы при этом наблюдатель оставался неподвижным относительно часов. Иначе возникнут те же недоразумения, что и при определении одновременности событий.
А как сравнить двое часов, если одни из них движутся относительно других равномерно и прямолинейно? Показания движущихся друг относительно друга часов можно непосредственно сравнить только в тот момент, когда они находятся в одном и том же месте, т. е. когда они проходят друг мимо друга. Чтобы сравнить ход часов, следует через некоторое время провести еще одно сравнивание. Только тогда увидим, какие часы шли медленнее, какие быстрее. Для второго сравнения часов придется воспользоваться уже более сложным методом. Поясним это (рис. 25).
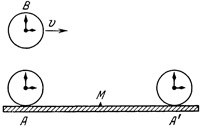 Рис. 25. Если часы В движутся относительно часов А, то для сравнения их хода нужно использовать вспомогательные часы A` неподвижные относительно часов А Рис. 25. Если часы В движутся относительно часов А, то для сравнения их хода нужно использовать вспомогательные часы A` неподвижные относительно часов А
Возьмем двое часов А и А`, неподвижных относительно нас. Пусть часы В перемещаются относительно часов А и А` равномерно и прямолинейно. Синхронизируем часы А и А`, т. е. поставим их стрелки так, чтобы они находились одновременно в одинаковых положениях (или, как говорят, «сверим часы»). Это значит, что если бы неподвижный наблюдатель М находился на равных расстояниях от часов А и А’ то он видел бы, что эти часы показывают одно и то же время. Расположимся теперь возле часов А и в тот момент, когда часы В пройдут мимо часов А, сравним их показания. Через некоторое время часы В пройдут мимо часов А`. В тот момент, когда это произойдет, мы и здесь произведем сравнение часов. Так как часы А` идут синхронно с часами А, то тем самым мы косвенно второй раз сравнили часы А и В. Теперь уже можно решать, насколько различаются скорости течения времени в разных инерциальных системах, связанных с часами А и В.
Читателю вся эта сложная система сравнения часов может показаться ненужной. У него может возникнуть такой вопрос: неужели действительно в разных инерциальных системах время может течь с различными скоростями? Может быть, на первый взгляд это и покажется крайне неправдоподобным, но все-таки дело обстоит именно так. Сравнение часов покажет, что для наблюдателя, находящегося у часов А, часы В идут медленнее, чем часы А. В движущейся инерциальной системе время течет медленнее, чем в покоящейся системе. Чтобы убедиться в сказанном, рассмотрим мысленно следующий опыт.
Пусть часы А и А` по-прежнему синхронизованы. Представим теперь, что в тот момент, когда часы В пройдут мимо часов А, от часов В испускается сигнал света. Пусть на своем пути сигнал встречает зеркало и, отразившись, возвращается к часам В как раз в тот момент, когда последние проходят мимо А`. Луч света вернулся в то же самое место, откуда он и отправлялся, т. е. к часам В (рис. 26).
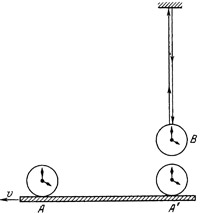 Рис. 26. Путь светового сигнала для наблюдателя, находящегося у часов В. На рисунке изображено расположение часов в момент возвращения светового сигнала Рис. 26. Путь светового сигнала для наблюдателя, находящегося у часов В. На рисунке изображено расположение часов в момент возвращения светового сигнала
В системе часов В луч света к зеркалу и обратно (от зеркала до часов В) пройдет по одной и той же прямой. Каким же будет путь луча света в системе отсчета часов А? Наблюдатель, находящийся у часов Л, увидит, что луч света испускается от часов А, а возвращается обратно к часам А`. В системе отсчета часов А луч света ю:рошел вдоль равных сторон равнобедренного треугольника (рис. 27), и его путь в этой системе, следовательно, был длиннее пути светового луча в системе отсчета часов В. Выше мы видели, что скорость света во всех инер-циальных системах одинакова и равна с, значит она будет равна с в системах отсчета, связанных и с часами А и с часами В. Отсюда следует, что относительно часов В луч света находился в пути меньшее время, чем относительно часов А, т. е. часы В успели отсчитать меньшее время. Значит, движущиеся часы В идут медленнее, чем покоящиеся часы А.
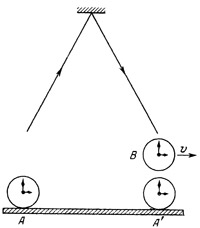 Рис. 27. Путь светового сигнала для наблюдателя, находящегося у часов А. На рисунке изображено расположение часов в момент возвращения светового сигнала Рис. 27. Путь светового сигнала для наблюдателя, находящегося у часов А. На рисунке изображено расположение часов в момент возвращения светового сигнала
Нетрудно вывести формулу зависимости хода часов от скорости их движения.
Пусть t0 — измеряемый в системе часов А промежуток времени, необходимый световому сигналу, чтобы пройти расстояние от часов В до зеркала и обратно. Время, в течение которого луч света находится в пути, в системе отсчета, связанной с часами B, обозначим через t. В равнобедренном треугольнике на рис. 28 равные стороны представляют собой путь луча света, изображенный на рис. 27, а высота — путь луча света, изображенного на рис. 26. Основание этого треугольника равно расстоянию, которое часы В прошли за время, дока луч света находился в пути; длина основания, следовательно, будет равна vto. Общая длина двух сторон треугольника равна пути, который свет прошел за to сек. Следовательно, длина одной стороны будет 1/2 cto. Расстояние зеркала
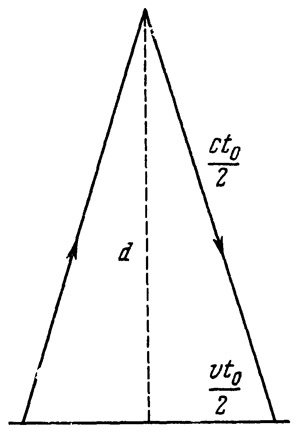 Рис. 28. Путь светового луча от часов В до зеркала и обратно для наблюдателя у часов А (сплошная линия) и для наблюдателя у часов В (пунктирная линия) Рис. 28. Путь светового луча от часов В до зеркала и обратно для наблюдателя у часов А (сплошная линия) и для наблюдателя у часов В (пунктирная линия)
от часов В (зеркало считается неподвижным относительно часов В) в системе отсчета часов А равно

Мы получим формулу, которая показывает, как промежуток времени, измеренный движущимися со скоростью v часами В, связан с промежутком времени t0, измеренным покоящимися часами А и А`. Каждые часы измеряют время в связанной с ними системе отсчета. Следовательно, в системе часов В время течет медленнее (промежуток между событиями короче), чем в системе, связанной с часами А.
У читателя теперь может возникнуть впечатление, что, развивая теорию относительности, мы зашли в тупик. В самом деле, как же все инерциальные системы могут быть равноправными, если в одной из них время течет быстрее, а в другой медленнее? Получается, будто мы можем найти систему отсчета, в которой время течет быстрее, чем во всех остальных. Эта система была бы, очевидно, в исключительном положении по сравнению с другими системами, что противоречит принципу относительности. В действительности же никакого противоречия не возникает.
В приведенном выше примере наблюдатель был неподвижным относительно часов А и А` (иначе он не смог бы синхронизировать эти часы). Сравнивая ход часов А и В, т, е. скорости течения времени в связанных с ними системах отсчета, он пришел к выводу, что движущиеся часы В идут медленнее покоящихся часов А. Рассмотрим теперь, к какому выводу о ходе часов придет наблюдатель, неподвижный относительно часов В. Чтобы сравнить ход часов А и? В, у него тоже должны быть вспомогательные часы. Может ли он в качестве вспомогательных часов использовать часы А`? Простое рассуждение показывает, что не может.
Часы А и А` были синхронизированы наблюдателем, неподвижным по отношению к ним. Это значит, что для наблюдателя, находившегося посередине между часами А и А` стрелки этих часов были одновременно в одинаковых положениях. Но в предыдущем параграфе мы выяснили, что одновременность событий — понятие относительное: события, одновременные, например, для наблюдателя в системе часов А не будут одновременными в системе часов В. Для наблюдателя в системе отсчета часов В стрелки часов А и А` будут находиться в одинаковых положениях в разные моменты времени и ими пользоваться для сравнения нельзя. Если наблюдатель, неподвижный относительно часов В, хочет сравнить ход часов А и В, он должен взять вспомогательные часы В` неподвижные и синхронные по отношению к часам В. Рассуждая дальше так же, как это мы уже делали выше, мы сможем убедиться в том, что часы А идут медленнее часов В.
Следовательно, для наблюдателя, неподвижного относительно часов А, часы A идут быстрее часов В; для наблюдателя же, неподвижного относительно часов В, часы В идут быстрее часов А. Тем самым инерциальные системы отсчета, связанные с часами А и В, находятся в совершенно одинаковых условиях. В обоих случаях имеет место один и тот же закон природы: часы, неподвижные относительно системы, идут быстрее всех; движущиеся же часы идут тем медленнее, чем больше их скорость в данной системе [см. формулу (3)]. Значит мы не нарушили принципа относительности, который требует равноправности всех систем отсчета.
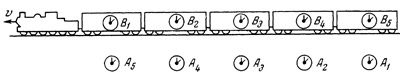 Рис. 29. Сравнение скорости течения времени в различных инер-циальных системах. На рисунке изображено положение, когда наблюдатель в поезде сравнивает часы А1 и B5, а наблюдатель на земной поверхности — часы В1 и А5 Рис. 29. Сравнение скорости течения времени в различных инер-циальных системах. На рисунке изображено положение, когда наблюдатель в поезде сравнивает часы А1 и B5, а наблюдатель на земной поверхности — часы В1 и А5
Предположим теперь, что мы сравниваем течение времени на земной поверхности и в поезде, движущемся равномерно и прямолинейно, например со скоростью 198450 км/сек относительно земной поверхности (такое большое значение скорости возьмем для наглядности расчета). Один из наблюдателей пусть находится на земле, другой — в поездке. Наблюдатель на Земле пусть синхронизирует все земные часы —-A1, А2, А3 и т. д. (рис. 29), а наблюдатель в поезде пусть синхронизирует все часы поезда — B1, B2, B3 и? т. д. Пусть наблюдатель на земле сравнивает часы поезда B1 со всеми своими часами. Предположим, что в тот момент, когда часы B1 прошли мимо часов А2, и те и другие показывали ровно час, а в момент, когда часы B1 минуют часы А2, последние показывают точно два часа. Сколько будут показывать часы поезда B1 когда они будут проходить мимо часов А2? По формуле (3) оказывается: если покоящиеся часы отсчитали один час, то по часам, движущимся со скоростью 198 450 км/сек, прошло только 45 минут. Значит, при встрече часов B1 и А2 первые из них показывают один час 45 мин вместо двух часов.
Для наблюдателя на земной поверхности время в поезде течет медленнее, чем время на земной поверхности. Для наблюдателя в поезде, наоборот, время на земле течет медленнее времени в поезде. В кажущейся противоречивости этих выводов выражается закон природы, согласно которому скорость течения времени не является абсолютным понятием. О скорости течения времени в заданной инерциальной системе можно говорить только тогда, когда фиксирована другая система, относительно которой мы эту скорость измеряем. В этом отношении скорость течения времени сходна со скоростью движения тела в пространстве. О скорости тела тоже можно говорить только тогда, когда указывается система отсчета, относительно которой измеряется скорость. Говоря о скорости, всегда нужно указывать, скорость какого тела мы имеем в виду и относительно какой системы отсчета мы ее измеряем. Говоря о времени, также всегда следует указывать, время какой инерциальной системы мы рассматриваем и относительно какой инерциальной системы мы измеряем это время.
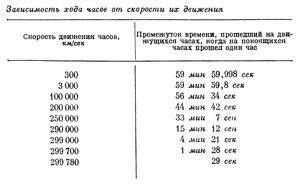
Зависимость хода часов от скорости их движения в пространстве описывается формулой (3). Для более конкретной характеристики этой зависимости составлена табл. 2. Из таблицы видно, что даже для таких больших скоростей, как 300 км/сек, движущиеся часы отстают от покоящихся только на 0,002 секунды в час; обычно в технике мы имеем дело со скоростями, не превышающими 10 км/сек, следовательно, это отставание будет еще намного меньше. Поэтому зависимость хода часов от скорости их движения не бросается в глаза. В случае же микрочастиц, перемещающихся с огромными скоростями, эта разница ощутима. Более наглядно данные табл. 2 представлены на графике (рис. 30). По горизонтальной оси откладывается скорость движущихся часов в км/сек, по вертикальной отложены промежутки времени по движущимся часам, если покоящиеся часы отсчитывают 60 мин.
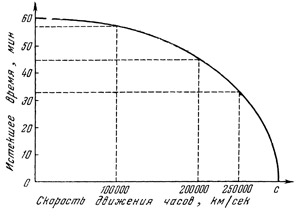 Рис. 30. Зависимость хода часов от скорости их движения Рис. 30. Зависимость хода часов от скорости их движения
Классическая механика изучает только медленные движения. Это значит, что часы во всех системах отсчета практически будут идти одинаково. Следовательно, нет нужды иметь часы в каждой системе отсчета. Достаточно одних часов, которые измеряют время во всех системах отсчета. В теории относительности, которая изучает движения с большими скоростями, часы в каждой системе отсчета идут по-своему. Теория относительности не может пользоваться «универсальными часами». Это, в частности, отражает тот факт, что в теории относительности невозможно разделить пространство и время.
Тела в природе изменяются с течением времени. Так, например, железо ржавеет, дерево гниет, радиоактивные вещества, распадаясь, превращаются в другие элементы и т. д. Скорость этих процессов зависит от скорости течения времени, следовательно, она зависит от скорости движения тела относительно наблюдателя. Если тело неподвижно, то с точки зрения наблюдателя время там течет с максимальной скоростью.
Другими словами: если тело не движется относительно наблюдателя, по помещенные на теле часы буду идти с максимальной скоростью. Время, измеряемое неподвижными относительно тела часами, называется собственным временем этого тела.
В повседневной практике мы измеряем время часами, находящимися на Земле, т. е. пользуемся собственным временем Земли. В этой связи у нас появляется склонность приписывать собственному времени Земли универсальное значение. Нередко люди считают, что в мировом пространстве, на всех небесных телах и у всех элементарных частиц время течет так же, как и на Земле. Приведенные в этом параграфе теоретические соображения показывают, что это не так.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 Рис. 25. Если часы В движутся относительно часов А, то для сравнения их хода нужно использовать вспомогательные часы A` неподвижные относительно часов А
Рис. 25. Если часы В движутся относительно часов А, то для сравнения их хода нужно использовать вспомогательные часы A` неподвижные относительно часов А Рис. 26. Путь светового сигнала для наблюдателя, находящегося у часов В. На рисунке изображено расположение часов в момент возвращения светового сигнала
Рис. 26. Путь светового сигнала для наблюдателя, находящегося у часов В. На рисунке изображено расположение часов в момент возвращения светового сигнала Рис. 27. Путь светового сигнала для наблюдателя, находящегося у часов А. На рисунке изображено расположение часов в момент возвращения светового сигнала
Рис. 27. Путь светового сигнала для наблюдателя, находящегося у часов А. На рисунке изображено расположение часов в момент возвращения светового сигнала Рис. 28. Путь светового луча от часов В до зеркала и обратно для наблюдателя у часов А (сплошная линия) и для наблюдателя у часов В (пунктирная линия)
Рис. 28. Путь светового луча от часов В до зеркала и обратно для наблюдателя у часов А (сплошная линия) и для наблюдателя у часов В (пунктирная линия)
 Рис. 29. Сравнение скорости течения времени в различных инер-циальных системах. На рисунке изображено положение, когда наблюдатель в поезде сравнивает часы А1 и B5, а наблюдатель на земной поверхности — часы В1 и А5
Рис. 29. Сравнение скорости течения времени в различных инер-циальных системах. На рисунке изображено положение, когда наблюдатель в поезде сравнивает часы А1 и B5, а наблюдатель на земной поверхности — часы В1 и А5
 Рис. 30. Зависимость хода часов от скорости их движения
Рис. 30. Зависимость хода часов от скорости их движения