| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
9. Теория относительности и геометрия
Классическая механика считала относительной (т. е. зависящей от выбора системы отсчета) скорость. Специальная теория относительности добавила сюда еще промежуток времени и расстояние в пространстве. Вследствие этого ряд понятий, которые мы привыкли считать абсолютными, при ближайшем рассмотрении оказывается относительным. Это относится, в частности, к форме тела. Проиллюстрируем сказанное некоторыми примерами.
Изготовим куб, длина ребра которого равна 1 м, и поставим его на землю (рис. 34). Предположим, что над кубом в направлении ребра АВ с большой скоростью проносится самолет. Если летчик измерит размеры куба, то он обнаружит, что ребра куба АВ, EF, DC и EG короче остальных восьми. Таким образом, по мнению летчика, на земле будет стоять не куб, а прямоугольный параллелепипед. Тело, которое в инерциальной системе Земли представляет собой куб, в системе самолета будет прямоугольным параллелепипедом, причем размеры последнего будут зависеть от скорости самолета относительно Земли.
Сказанное выше имеет место не только для шестигранника, но и для тела любой формы. Форма тела всегда зависит от направления и скорости движения. Например, в одной инерциальной системе тело может иметь форму шара, в другой же — форму эллипсоида; в одной системе тело может быть цилиндром вращения, в другой — эллиптическим цилиндром. Форма тела относительна. Только число граней не относительно. Шестигранник всегда останется шестигранником, в какой бы инерциальной системе мы его ни рассматривали. Если относительны размеры и форма тела, то, естественно, относительным будет и его объем. Объем тела, движущегося со скоростью v, будет в √(1 - v2/c2) раз меньше объема точно такого же покоящегося тела Пусть дан круг, радиус которого равен а. Площадь круга равна, как известно, πа2. Представим теперь, что круг начинает двигаться в направлении, указапном на рисунке 35. Тогда, согласно формуле (б), площадь круга станет равной СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

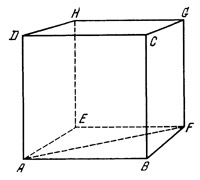

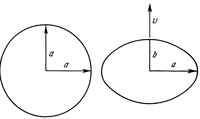 Рис. 35. Если неподвижная фигура является окружностью, то движущаяся будет эллипсом
Рис. 35. Если неподвижная фигура является окружностью, то движущаяся будет эллипсом