Главная >> В мире больших скоростей >> Специальная теория относительности 13. Четырехмерный мир
Вы позвали электрика и просите его подвесить к потолку электрическую лампу. Пусть эта лампа должна находиться на расстоянии 3 м от одной стены и 4 м от смежной стены на высоте 2 м от пола. Этой просьбы электрику достаточно. Он не станет допытываться у вас, как далеко должна находиться лампа от дивана или от письменного стола, потому что эти данные ему уже не нужны. Положение лампы в комнате точно определяется тремя числами. Эти три числа не обязательно должны быть именно такими, какие приводились выше. Вы могли задать другие «ориентиры», указать, например, на сколько электрическая лампа должна отстоять от двух углов и потолка. Существенно только, что для точного определения положения лампы вам необходимо задать три числа.
Рассмотрим другой пример. Вы просите мастера изготовить маленький ящичек. При этом вы непременно указываете размеры ящика: длину, ширину и высоту — опять-таки три числа. На вопрос, сколько прямых можно провести через заданную точку пространства так, чтобы все они были перпендикулярны между собой, вы дадите определенный ответ: три прямые.
В том, что во всех приведенных примерах существенную роль играет число три, выражается трехмерность нашего пространства. У пространства три измерения. Почему же именно три, а не два или четыре, относительно этого мы ничего не можем сказать. Нужно просто раз и навсегда принять во внимание, что основным свойством окружающего нас пространства является его трехмерность.
Нужно, однако, иметь в виду, что описание мира в виде собрания трехмерных предметов не отвечает действительности. Такое описание давало бы нам застывшую, мертвую картину мира, в то время как в действительном мире все движется и изменяется. Это значит, что при описании мира следует описывать не предметы, а события. Событие же определяется уже не тремя, а четырьмя числами (координатами): три числа определяют место происхождения события, а четвертое — момент времени, в который событие происходит.
Множество всех пространственных точек образует пространство. Чтобы выделить некоторую точку пространства (например, точку, в которой мы хотим видеть в своей комнате электрическую лампу), нужно задать три числа. Аналогично, множество всевозможных событий — происшедших, совершающихся и грядущих — образует движущийся и изменяющийся реальный мир. Чтобы в этом мире отделить одно событие от другого, необходимо задать четыре числа. Математики в таком случае говорят, что мир событий — четырехмерный. Этот четырехмерный мир событий называют также миром пространства — времени.
Математики обычно пытаются все вопросы рассматривать в возможно более общем виде. Они, например, не довольствуются тем, что мир непременно должен быть трехмерным, а спрашивают: какими свойствами будет обладать пространство, если размерность его будет больше трех? Так, в математике изучены свойства пространств с четырьмя, пятью и даже большим числом измерений. Оказывается, что, например, в четырехмерном пространстве через одну точку возможно провести четыре прямые, перпендикулярные друг к другу. Естественно, что человеку трудно наглядно представить четырехмерное геометрическое пространство, так как все его представления неизбежно связаны с тремя измерениями. Но это вовсе не значит, что вообще нельзя пользоваться понятием четырехмерного пространства. Изучение и применение геометрических свойств четырехмерного пространства принципиально ничуть не сложнее, чем трехмерного. Для сравнения вспомним, что изучаемая в школе планиметрия представляет собой описание геометрических свойств двухмерного пространства. Планиметрия служила бы нам вместо стереометрии в том случае, если бы все окружающие нас предметы вместо трехмерных оказались двухмерными.
У некоторых читателей может возникнуть вопрос: какую же пользу приносит нам изучение геометрических свойств четырехмерного пространства, если действительное пространство — трехмерное? Оказывается, что математическое четырехмерное пространство может иметь такие же свойства, как физическое пространство — время. Таким образом, физики могут определять свойства мира событий по свойствам математического четырехмерного пространства. Такой геометрический метод исследований часто бывает наиболее простым и наглядным.
Французский математик и механик Ж. Л. Лагранж в свое время обратил внимание на то, что происходящие в природе движения можно описывать в четырехмерном пространстве-времени. Но так как в классической физике пространство и время рассматриваются совершенно обособленно друг от друга, то их объединение в пространство-время было чисто формальным приемом. Иначе обстоит дело в теории относительности. Так как эта теория учитывает связь между пространством и временем, то их объединение приобретает глубокое содержание.
В 1908 г. Г. Минковский изложил всю теорию относительности с помощью геометрии четырехмерного мира событий. Представление Минковского дало возможность изображать все положения теории относительности в виде очень простых геометрических схем. Эта простота вовсе не случайна, она обусловлена именно тем, что пространство и время образуют единое четырехмерное пространство-время.
На первый взгляд такое утверждение может показаться непостижимым. Как можно соединять в теории пространство и время, если они измеряются различными приборами и выражаются различными единицами: пространственные расстояния измеряем, например, в метрах, а промежутки времени — в секундах. Более глубокое рассмотрение, однако, показывает, что делать такое разделение вовсе не обязательно — можно расстояния измерять в секундах, или, наоборот, время — в метрах. Это и делается весьма часто на практике.
Так, например, часто пешеход спрашивает: «Далеко ли до города?» В ответ раздается. «Около часа пути». В этом ответе длина пути измерена единицей времени — часом. Астрономический световой год представляет также единицу измерения космических расстояний, выраженную в годах.
Часто поступают и наоборот, т. е. время измеряют в единицах длины. Когда шофер объявляет: «Бензина хватит ненадолго, самое большее на десяток километров», то он здесь для измерения времени использует километры.
Читатель заметит, что выражение «час пути» может означать три, четыре или пять километров — в зависимости от того, как быстро шагает пешеход. Существенна скорость движения также и при измерении времени в километрах. Если используемая для измерения скорость определяется не точно, то от описанного способа нельзя ожидать большой точности. Напротив, если имеем дело с определенной скоростью, то измерение времени в единицах длины и измерение расстояний в единицах времени производится точно. Так как скорость света — определенная величина, то, например, астрономический световой год фиксируется вполне точно — он равен 9 460 000 млн. км.
В то время как астрономы измеряют расстояния в единицах времени (световой год), в теории относительности поступают обычно наоборот: в единицах длины измеряют время. Вместо того, чтобы сказать «одна секунда», говорят «300 000 км» — это расстояние, которое световой луч в пустоте проходит за 1 сек. Так вводится в употребление единица времени, которую мы можем назвать световым километром. Световой километр — это время, необходимое световому лучу для прохождения 1 км. 1 сек следовательно, составит 300 000 световых км.
Интересный метод измерения времени в единицах длины используется на станциях оптического наблюдения за искусственными спутниками. На магнитофонную ленту записываются удары хронометра. На эту же ленту фиксируется сигнал, который дает наблюдатель в тот момент, когда спутник попадает в поле зрения телескопа. За 1 сек магнитофонная лента продвигается на 38,5 см. Это значит, что каждый секундный удар хронометра отмечается на ленте на расстоянии 38,5 см от предыдущего. Измеряя на магнитофонной ленте расстояние сигнала, определяющего момент прохождения спутника, от секундных сигналов хронометра, можем определить момент прохождения спутника. Поскольку скорость магнитофонной ленты известна, такой способ измерения времени с помощью единиц длины достаточно точен.
Если мы хотим измерять время в световых километрах, то систему отсчета нужно представить в виде тела, снабженного источником света и масштабом длины. Измерение времени осуществляется тогда посредством измерения пути, пройденного сигналом света.
Приведем теперь основные идеи трактовки теории относительности Минковским.
 Герман Минковский
ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ИНЕРЦИАЛЬНОЙ СИСТЕМЫОдну определенную инерциальную систему можно представить в виде двух перпендикулярных друг другу прямых, как показано на рис. 37. Горизонтальную прямую r назовем пространственной осью. Каждая точка этой прямой означает какую-то точку пространства. От начала оси отложена единица длины, которой пользуемся при измерениях в пространстве. Вертикальная прямая носит название временной оси; каждой точке этой оси соответствует определенный момент времени. Время при этом измеряем описанным выше способом в световых километрах. У начала временной оси также нанесена единица измерения, которая взята равной пространственной единице измерения. Изображенные на рисунке перпендикулярные прямые и единицы измерения образуют геометрическое изображение системы отсчета. Рассмотрим теперь, как в этой системе изображаются события.
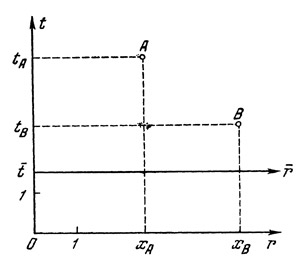 Рис. 37. Геометрическое изображение инерциальной системы отсчета
Пусть в некоторый момент tА в точке пространства хА произошло какое-то событие. Чтобы нанести изображение этого события на нашем рисунке, проведем из точек tА и хА прямые, паралдельные осям. Место пересечения этих линий, которое мы обозначим через А, и изобразит событие. Наоборот, если мы зафиксируем некоторую точку В на рисунке, то сразу же можем найти, что эта точка соответствует событию, которое произошло в пространственной точке хв в момент времени tв. Точка О определяет положение тела отсчета в нулевой момент времепи, т. е. в тот момент, когда отправляется сигнал света, используемый для измерения времени.
Горизонтальная прямая, обозначенная через г, соответствует изображениям всех пространственных точек в нулевой момент времени. Другая горизонтальная прямая, обозначенная через г¯, соответствует изображениям всех пространственных точек в момент времени t¯.
Пространственное расстояние между событиями А и В определяется, очевидно, длиной отрезка между точками хА и хB, а промежуток времени между этими событиями — длиной отрезка между точками tА и tB.
ПЕРЕХОД В НОВУЮ ИНЕРЦИАЛЬНУЮ СИСТЕМУУ читателя может возникнуть естественный вопрос: чем отличается геометрическое изображение одной инерциальной системы от другой? Минковский показал, что разница здесь только в направлениях временных и пространственных осей. Переход из одной инерциальной системы в другую описывается просто наклонением осей, причем точка пересечения осей остается на месте. На рис. 38 одна инерциальная система изображается сплошной, другая — пунктирной линиями. Пространственная ось второй системы обозначена через r`, временная — через t`.
Минковский показал, что угол а между осями двух систем связан следующим образом с относительной скоростью v инерциальных систем
v/c = tg α (4)
Так как максимальное значение v равно с, то ясно, что наибольшее возможное значение α равно 45°, т. е. угол между осями инерциальных систем не должен превышать половины прямого угла.
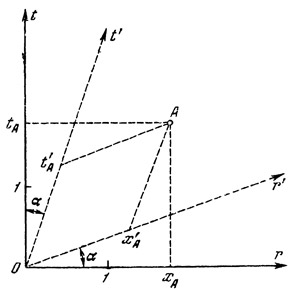 Рис. 38. Геометрическое изображение двух инерциальных систем, движущихся друг относительно друга
На рис. 38 изображено еще и событие А. В инерциальной системе с осями r и t место совершения события есть хA и время tA, а в системе с осями r` и t` — соответственно хA` и tA`.
Из геометрического представления инерциальных систем следуют все основные результаты релятивистской .кинематики, как, например, сокращение продольных размеров движущегося тела или замедление хода движущихся часов.
Однако здесь мы можем остановиться только па проблеме одновременности событий и проблеме совершения событий в одной точке пространства.
ОТНОСИТЕЛЬНОСТЬ ВРЕМЕННОГО И ПРОСТРАНСТВЕННОГО ЧЕРЕДОВАНИЯ СОБЫТИЙ Рассмотрим изображенные на рис. 39 события А и В, моменты времени которых в инерциальной системе с осями r и t будут соответственно tA и tB. Моменты совершения этих же событий в системах с осями r`, t` и r", t`` будут соответственно tA` и tB` и tA`` и tB``. Так как tA` = tB` то в инерциальной системе r`, t` события А и В будут одновременными. В системе r, t эти события не будут одновременными — событие А происходит (раньше события В (tA<tB). Напротив, в инерциальной системе r", t" событие В происходит раньше события A (tA">tB"). Отсюда следует, что события, одновременные в одной инерциальной системе, не будут одновременными в другой инерциальной системе. При переходе из одной инерциальной системы в другую можно изменить также временную последовательность событий. Для читааеля, по-видимому, не представит труда сделать рисунок, из которого было бы видно, что события, происходящие в некоторой инерциальной системе в одной точке пространства, в другой инерциальной системе совершаются в разных точках.
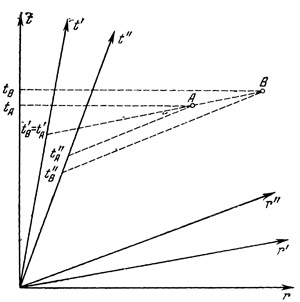 Рис. 39. Относительность одновременности.
Момент события А в системе отсчета г", t" получим, проведя через точку А прямую, параллельную оси г". Точка пересечения этой прямой с осью t" дает момент события t``A. Аналогично найдем моменты событий А и Б во всех трех инерциальных системах, На рисунке видно, что события А и Б одновременны в системе г`, t`, тогда как в других системах они не являются таковыми
ПРОШЛОЕ, НАСТОЯЩЕЕ, БУДУЩЕЕЧто мы понимаем под настоящим? Это весь мир в один и тот же определенный момент времени, а именно: в настоящий момент. Настоящее состоит из всех событий, происходящих в данный момент. Точки, изображающие такие события, образуют пространственную ось.
Каждая инерциальная система имеет свою пространственную ось. Это значит, что в каждой инерциальной системе под настоящим понимаются разные события: в одной инерциальной системе это будут события, образующие ось r, в другой — ось r`. Настоящее в одной системе не будет .настоящим в другой. Настоящее является относительным понятием. Точно так же относительными могут быть и прошлое и будущее, это показывает возможность изменить [временную последовательность событий при переходе из одной инерциальной системы в другую.
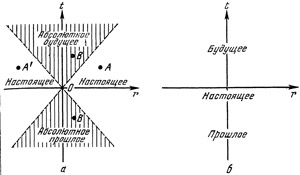 Рис. 40. Схема будущего, настоящего и прошедшего в теории относительности (а) и в классической физике (б)
Все события, которые изображены точками верхней заштрихованной части плоскости, образует абсолютное будущее относительно события О. Все события, которые изображаются точками нижней заштрихованной части плоскости, образуют относительно события О абсолютное прошлое. Точки незаштрихованной части плоскости образуют события, происходящие относительно события О в настоящем. В классической физике настоящее изображается пространственной осью, будущее — верхней полуплоскостью, прошедшее — нижней полуплоскостью
Однако теория относительности признает и абсолютное прошлое и абсолютное будущее. Обсуждая выше вопрос о причине и следствии, мы видели, что переходом из одной инерциальной системы в другую невозможно изменить временную последовательность всех пар событий. Полученные там условия теперь можно сформулировать следующим образом.
Еcли пространственная удаленность событий меньше промежутка времени между событиями (измеренного в световых километрах), то временная последовательность таких событий во всех инерциальных системах будет одинаковой. Если же пространственная удаленность событий больше промежутка времени между событиями (опять-таки измеренного в световых километрах), то переходом из одной инерциальной системы в другую возможно изменить временную последовательность этих событий. С помощью геометрического изображения инерциальных систем нетрудно убедиться в сказанном. На рис. 40, а изображены пять событий: О, А, А`, В и С. Видно, что пространственное расстояние между событиями О и A (а также О и А`) больше временного.
Для пар событии О и В (а также О и С), наоборот, временное расстояние больше пространственного. При переходе из одной инерциальной системы в другую оси можно наклонять только на угол (одинаковый для обеих осей) меньше 45°, т. е. оси можно наклонять только так, чтобы они не перешли через пунктирную прямую, изображенную на рисунке. Из рисунка видно, что невозможно найти такую инерциальную систему (т. е. невозможно так наклонить оси), чтобы события О и А (а также О и A`). B новой системе происходили бы в одной и той же точке пространства, а события О и В (а также события О и С) были бы одновременными. Событие В во всех инициальных системах происходит после события О, т. е. событие В находится по отношению к событию О в абсолютном будущем. Аналогично, событие С совершается относительно события О в абсолютном прошлом.
Относительно событий А и А` невозможно сказать, происходят они в будущем или в прошлом относительно события О: в одной инерциальной системе у них одна временная последовательность, в другой — иная. Следовательно, эти события следует считать происходящими в настоящем относительно события О.
На рис. 40, а показано соотношение между абсолютным будущим, абсолютным прошлым и настоящим в теории относительности. Все точки верхней части плоскости, заключенной между пунктирными прямыми, изображают абсолютное будущее относительно события О. Все точки, заключенные между пунктирными прямыми в нижней части плоскости, составляют абсолютное прошлое относительно событий О. И, наконец, по правую и левую стороны от пунктирных прямых остаются части плоскости, изображающие настоящее.
Для сравнения на рис. 40, б представлена связь будущего, прошлого и настоящего в классической физике. Здесь настоящее представляет лишь мгновение между прошлым и будущим — настоящее описывает только прямая r, а прошлое и будущее занимают каждая по полуплоскости. В теории относительности часть плоскости, изображающая настоящее, симметрична относительно частей, составляющих будущее и прошлое. Это, впрочем, не значит, что теория относительности будто бы описывает «больше» событий, чем классическая физика. В области математики, которая называется теорией множеств, доказано, что множество точек прямой имеет такую же мощность, как и множество точек плоскости. Образно говоря, прямая содержит в себе «столько же точек», сколько и плоскость. Следовательно, множества событий в теории относительности и в классической физике «одинаково бесконечны». Только связи между событиями теория относительности описывает точнее и в более симметричном виде, чем это делает классическая физика.
Геометрическое изображение инерциальных систем отчетливо показывает, как пространство и время образуют единое целое. При переходе из одной инерциальной системы в другую происходит, образно говоря, операция перевода «чего-то» со счета пространства на счет времени и наоборот. Отсюда следует, что реальный мир представляет собой четырехмерное пространственно-временное целое, которое, отражаясь в нашем сознании, создает представление о пространстве и времени. В рамках одной инерциальной системы пространство отделено от времени, но при рассмотрении многих систем эта обособленность теряется. Переходя из одной инерциальной системы в другую (т. е. изменяя скорость движения), человек непосредственно должен был бы обнаружить связь между временем и пространством. К сожалению, эта взаимосвязь становится практически заметной только при сверхгигантских изменениях скорости, поэтому человеку никогда не удастся убедиться в существовании этой связи непосредственно. Что связь пространства и времени все же существует, подтверждается прекрасным согласием теории относительности с опытными данными.
Разумеется, не следует понимать сказанное так, будто бы пространство и время в теории относительности представляют собой явления с одинаковыми свойствами, и что эти явления можно произвольно заменять одно другим. Существенным различием является уже то, что время имеет одно измерение, а пространство трехмерно. Кроме того, есть еще и другие различия.
Теория относительности признает абсолютное прошлое и абсолютное будущее. Это значит, что переходом из одной инерциальной системы в другую нельзя изменить направление течения времени. Время — это явление с определенным направлением, преобразование прошлого в будущее и будущего в прошлое невозможно.
Согласно современным данным, пространство не имеет такого свойства. В принципе все пространственные направления во Вселенной равноправны. Конкретные условия (например, сила тяжести, электрическое поле и т. д.) могут, правда, образовать предпочтительные направления в пространстве, но это не меняет общего принципа.
Сила тяжести определяет в каждом месте Земли предпочтительное направление. Гравитационная сила Солнца определяет предпочтительные направления в границах Солнечной системы и т. д. Но в самой Вселенной предпочтительных направлений нет, все практически проявляющиеся предпочтительные направления определяются местными физическими причинами. Это значит, что результаты физических опытов не зависят от того, как ориентирована аппаратура в пространстве (разумеется, в случае, если задачей опыта не является определение местных предпочтительных направлений — силы тяжести, магнитного поля Земли и т. п.).
Пространство обладает и другим интересным свойством — равноправностью всех точек .пространства. Не существенно, в каком месте мы проводим физический опыт— результат его будет одним и тем же. Например, второй закон Ньютона действует одинаково в любой точке Вселенной. Измерение длин в пространстве тоже можем производить в любом месте, все равно получим правильный результат.
Аналогичное свойство имеет и время: все моменты времени равноправны. Физические законы одинаковы для всех времен. Не существенно, в какой момент мы заведем часы, все равно они начнут показывать время правильно, если только сами часы исправны.
О равноправности всех инерциальных систем, как об одном из основных требований физики, мы уже говорили выше. Теперь к этому надо добавить еще следующие выводы: равноправность всех направлений в пространстве, равноправность всех точек пространства и равноправность всех моментов времени.
Таковы основные требования, поставленные природой, которым должны удовлетворять все физические теории. Кстати, эти требования отображены в геометрическом представлении теории относительности.
Четырехмерный мир событий вовсе не является чем-то мистическим, это реальное целое, существующее в природе. Этим не утверждается, однако, что предметы должны быть четырехмерными. Предметы есть и будут трехмерными, но действительный мир состоит не из предметов, а из событий, происходящих с этими предметами. Именно в этом и проявляется движение и изменение материи.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|
