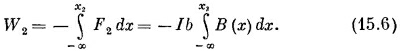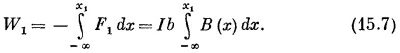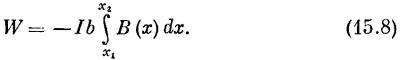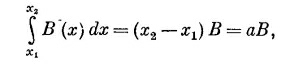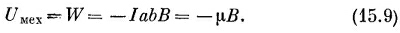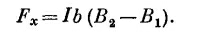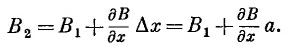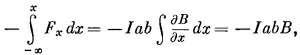| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Силы, действующие на петлю с током. Энергия диполя
В предыдущей главе мы изучали магнитное поле, создаваемое маленькой прямоугольной петлей, по которой течет ток. Мы нашли, что это поле диполя с дипольным моментом, равным
где / — сила тока, a A — площадь петли. Момент направлен по нормали к плоскости петли, так что можно писать и так:
Их плечо равно
или, поскольку lab — магнитный момент петли,
Вращательный момент может быть записан и векторно:
То, что вращательный момент дается уравнением (15.2), мы показали пока только для довольно частного случая. Но результат, как мы увидим, верен для маленьких петель любой формы. Полезно напомнить, что и для вращательного момента, действующего на электрический диполь, мы получили соотношение подобного же рода:
Сейчас нас интересует механическая энергия нашей петли, по которой течет ток. Раз есть момент вращения, то энергия, естественно, зависит от ориентации петли. Принцип виртуальной же работы утверждает, что момент вращения — это скорость изменения энергии с углом, так что можно написать
Подставляя т =+μB sin θ и интегрируя, мы вправе принять за энергию выражение
(Знак минус стоит потому, что петля стремится развернуть свой момент по полю; энергия ниже всего тогда, когда (μ и В параллельны.)
Опять получилось соответствие с электрическим диполем, где
Только в (15.5) электрическая энергия — и вправду энергия, a Uмex в (15.4) — не настоящая энергия. Но все равно ее можно применять для расчета сил по принципу виртуальной работы. Надо только предполагать, что ток в петле (или по крайней мере магнитный момент μ) остается неизменным при повороте.
Подобно этому, и работа против сил, действующих на сторону 1, равна
Чтобы вычислить каждый интеграл, надо знать, как В(х) зависит от х. Но ведь сторона 1 при движении рамки расположена все время параллельно стороне 2 на одном и том же расстоянии от нее, так что в ее интеграл входит почти вся работа, затраченная на перемещение стороны 2. Сумма (15.6) и (15.7) на самом деле равна
Но, попав в область, где В на обеих сторонах 1 и 2 почти одинаково, мы имеем право записать интеграл в виде
где В — поле в центре петли. Вся вложенная механическая энергия оказывается равной
Это согласуется с выражением для энергии (15.4), выбранным нами прежде.
Если петля «узкая», т. е. если В2 и В1 не очень различаются между собой, то можно было бы написать
Так что сила была бы равна
Вся работа, произведенная внешними силами над петлей, равнялась бы
а это опять —μB. Но теперь нам становится понятно, почему получается, что сила, действующая на небольшую токовую петлю, пропорциональна производной магнитного поля, как это следовало ожидать из
Другой наш результат состоит в следующем. Хоть и не исключено, что не все виды энергии вошли в формулу Uмех = —μВ (ведь это просто некоторая имитация энергии), ею все же можно пользоваться, применяя принцип виртуальной работы, чтобы узнать, какие силы действуют на петли с постоянным током. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.


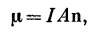
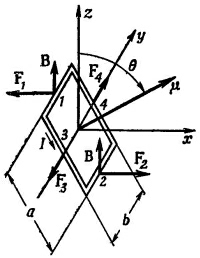 где n — единичный вектор нормали к площади А.
где n — единичный вектор нормали к площади А.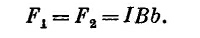
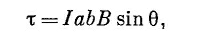
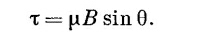

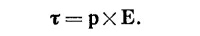
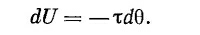
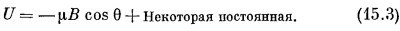


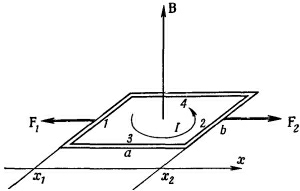 Вообразите, что мы хотим двигать петлю в направлении х, т. е. в ту область, где поле сильнее, и что петля ориентирована так, как показано на фиг. 15.2. Мы отправимся оттуда, где поле равно нулю, и будем интегрировать силу по расстоянию по мере того, как петля входит в поле.
Вообразите, что мы хотим двигать петлю в направлении х, т. е. в ту область, где поле сильнее, и что петля ориентирована так, как показано на фиг. 15.2. Мы отправимся оттуда, где поле равно нулю, и будем интегрировать силу по расстоянию по мере того, как петля входит в поле.