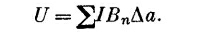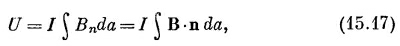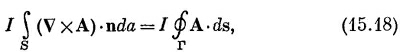| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Энергия постоянных токов
Зная, что Uполн = —Uмех, используем этот факт, чтобы найти истинную энергию постоянных токов в магнитных полях. Начать можно с истинной энергии небольшой токовой петельки. Обозначая Uполн просто через U, напишем
В пределе, когда петли становятся бесконечно малыми, сумма превращается в интеграл, и
где n — единичная нормаль к da.
где ds — линейный элемент вдоль Г. Итак, мы получили энергию контура произвольной формы:
В этом выражении А обозначает, конечно, векторный потенциал, возникающий из-за токов (отличных от тока / в проводе), которые создают поле В близ провода.
Это соответствует полученному для электростатической энергии выражению
Значит, мы можем считать А, если угодно, своего рода потенциальной энергией токов в магнитостатике. К сожалению, это представление не очень полезно, потому что оно годится только для статических полей. B действительности, если поля со временем меняются, ни выражение (15.20), ни выражение (15.21) не дают правильной величины энергии. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2025
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.


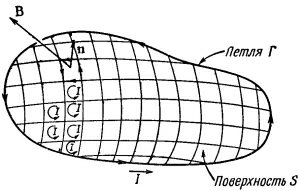 Хотя эту энергию мы подсчитали только для плоской прямоугольной петли, все это верно и для плоской петельки произвольной формы.
Хотя эту энергию мы подсчитали только для плоской прямоугольной петли, все это верно и для плоской петельки произвольной формы.