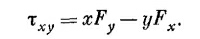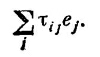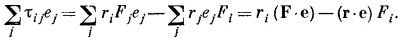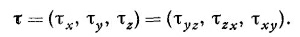Главная >> Фейнмановские лекции по физике >> Том 7 >> Глава 31. Тензоры

Векторное произведение

Сами того не подозревая, вы пользуетесь тензором второго ранга уже начиная с гл. 20 (вып. 2). В самом деле, мы определили там «момент силы, действующий в плоскости», например τ_xy  , следующим образом:

Обобщая это определение на три измерения, можно написать

Как видите, величина τ_¡j — это тензор второго ранга. Один из способов убедиться в этом — свернуть τ_¡j с каким-то вектором, скажем с единичным вектором е, т. е. составить

Если эта величина окажется вектором, то τ_¡j. должен преобразовываться как тензор — это просто наше определение тензора. Подставляя выражение для τ_¡j, получаем

Поскольку скалярные произведения, естественно, являются скалярами, то оба слагаемых в правой части — векторы, как и их разность. Так что τ_¡j — действительно тензор.
 
Однако τ_¡j принадлежит к особому сорту тензоров, он антисимметричен, т. е.

Поэтому у такого тензора есть только три разные и неравные нулю компоненты: т_xy , т_yz и т_zх. В гл. 20 (вып. 2) нам удалось показать, что эти три члена почти «по счастливой случайности» преобразуются подобно трем компонентам вектора; поэтому мы могли тогда определить вектор

Я сказал «по случайности» потому, что это происходит только в трехмерном пространстве. Например, для четырех измерений антисимметричный тензор второго ранга имеет шесть различных ненулевых членов, и его, разумеется, нельзя заменить вектором, у которого компонент только четыре.
 
Точно так же как аксиальный вектор т=r х F является тензором, по тем же соображениям тензором будет и любое векторное произведение двух полярных векторов. К счастью, они тоже представимы в виде вектора (точнее, псевдовектора), что немного облегчает нам всю математику.
 
Вообще говоря, для любых двух векторов а и b девять величин a_¡b_j образуют тензор (хотя для физических целей он не всегда может быть полезен). Таким образом, для вектора положения r величины r_¡r_j  являются тензором, а поскольку δ_¡j тоже тензор, то мы видим, что правая часть (31.20) действительно является тензором. Подобным же образом тензором будет и (31.22), так как оба члена в правой части — тензоры.

СМОТРИТЕ ТАКЖЕ: