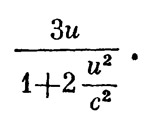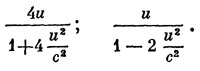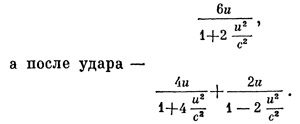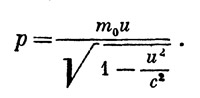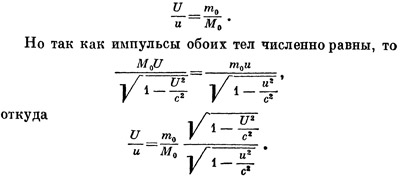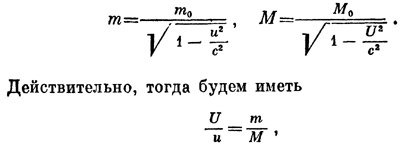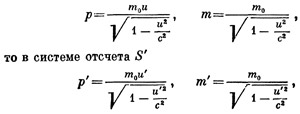Главная >> Введение в теорию относительности § 13. Масса и импульс. Формулы импульса.
До сих пор мы занимались исключительно пространственно-временными соотношениями, кинематикой теории относительности. Теперь нам предстоит познакомиться с основными положениями релятивистской динамики.
Прежде всего вспомним основные представления динамики классической, ньютоновской. Во-первых, считается, что свойства всякого материального тела, какова бы ни была его природа и внутренняя структура, позволяют приписать ему вполне определенные числовые значения ряда величин: массы, импульса, кинетической энергии и т. д. Во-вторых, взаимодействия между телами осуществляются посредством действующих между ними сил, которые также допускают точное числовое выражение. В-третьих, хотя в процессе движения значения всех этих величин и изменяются, но при этом они всегда удовлетворяют некоторым соотношениям, которые и выражают собой законы механики.
Так, второй закон Ньютона, лежащий в фундаменте классической динамики, утверждает, что изменение импульса какого-либо тела в течение промежутка времени t2—t1 всегда равно произведению величины этого промежутка на действующую на тело силу. Аналогичный смысл имеют и другие законы.
Различные физические законы обладают разной степенью общности. Одни из них применимы к сравнительно небольшому, узкому кругу явлений; для других область применимости более широка. В частности, физика сумела выявить и такие законы, которые справедливы всегда и везде, которые точнейшим образом соблюдаются буквально во всех явлениях. Важнейшими из них являются законы сохранения.
Законов этих в классической физике имеется три: закон сохранения массы, закон сохранения импульса и закон сохранения энергии. Они утверждают, что во всякой изолированной системе тел (т. е. такой системе, которая не взаимодействует ни с какими внешними телами) суммарные масса, импульс и энергия всех составляющих данную систему тел остаются постоянными.
В ньютоновской механике импульс р тела и его кинетическая энергия Т выражаются через массу m и скорость u следующим образом:
p = mu, T = mu2/2.
 Можно ли без всяких изменений перенести все эти законы и соотношения в.теорию относительности? Другими словами, совместимы ли они с релятивистской кинематикой? Легко убедиться, что ответ на этот вопрос будет отрицательным. В самом деле, рассмотрим хотя бы следующий простой пример. Можно ли без всяких изменений перенести все эти законы и соотношения в.теорию относительности? Другими словами, совместимы ли они с релятивистской кинематикой? Легко убедиться, что ответ на этот вопрос будет отрицательным. В самом деле, рассмотрим хотя бы следующий простой пример.
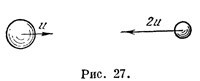
Пусть навстречу друг другу движутся два абсолютно упругих шара (рис. 27). Пусть масса одного шара ровно вдвое больше массы другого, а скорость его соответственно вдвое меньше. Тогда после столкновения оба шара будут двигаться с теми же скоростями, лишь переменив их направления на обратные — только при этом условии импульс и кинетическая энергия системы этих двух тел останутся неизменными.
Рассмотрим теперь то же самое движение в системе отсчета, где первый (более легкий) шар до удара неподвижен. Из закона сложения скоростей нетрудно получить скорости обоих шаров в этой новой системе отсчета. Обозначим через и абсолютную величину скорости второго шара в старой системе отсчета. Тогда до удара в новой системе отсчета скорость первого шара будет равна, конечно, нулю, а скорость второго —
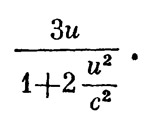 |
После удара скорости обоих шаров будут иметь одно и то же направление; величины их равны соответственно
Если массу первого шара принять за единицу, то масса второго шара будет равна двум единицам. Умножая эти массы на соответствующие скорости и складывая, получим суммарный импульс обоих шаров. До удара он оказывается равным
Это значит, что в новой системе отсчета закон сохранения импульса оказывается нарушенным.
Что же отсюда вытекает? Если мы желаем перенести законы сохранения в теорию относительности — а это сделать необходимо,— то для импульса и кинетической энергии следует поискать новые выражения, которые были бы полностью согласованы с релятивистской кинематикой. Для этого можно, рассматривая те или иные мысленные эксперименты в различных системах отсчета, подбирать формулы для импульса и энергии таким образом, чтобы законы сохранения выполнялись во всех системах отсчета одновременно. Ввиду некоторой сложности выкладок, мы их опускаем и приведем лишь окончательный результат. Оказывается, что единственно возможным выражением для релятивистского импульса является следующее:
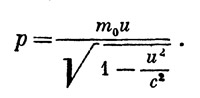 |
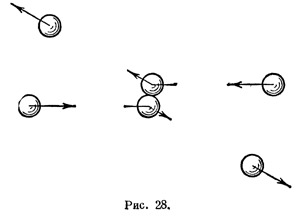
Для его вывода достаточно рассмотреть следующее движение двух абсолютно упругих шаров одинаковой массы (рис. 28). Шары сначала движутся друг другу навстречу с равными скоростями, а затем, столкнувшись, расходятся так, как показано на рисунке. Соображения, основанные на симметрии этого движения, показывают, что оно, во всяком случае, возможно. Тогда, рассматривая это движение в подходящих системах отсчета и требуя выполнения закона сохранения импульса, мы придем к вышеуказанному выражению.
Нужно отметить, что формула релятивистского импульса была впервые получена Эйнштейном из электродинамики Максвелла — Лоренца. К тому времени законы движения заряженных частиц в электромагнитном поле были изучены с достаточной полнотой. Анализ их с точки зрения теории относительности приводил неизбежно к такому же выражению.
При малых скоростях, как легко убедиться, эта формула практически совпадает с классической.
Интересно выяснить, как нарастает импульс при рассмотренном нами в предыдущем параграфе равноускоренном движении. Скорость изменяется согласно уравнению

показывающему, что при равноускоренном движении импульс нарастает пропорционально времени. Этот вывод вполне согласуется с нашими представлениями о равноускоренном движении; величину m0a с этой точки зрения следует рассматривать как силу. Впрочем, понятие силы нам в дальнейшем придется несколько уточнить.
Приведенные выше аргументы при всей их убедительности не могут, однако, рассматриваться как строгий вывод формулы релятивистского импульса. Нужно с полной ясностью отдать себе отчет в том, что чисто умозрительным путем доказать эту формулу невозможно, так же как невозможно доказать и классическую формулу р=ти. Ее надлежит рассматривать как опытный факт. То обстоятельство, что мы сумели получить ее без непосредственного обращения к опыту, этому высказыванию не противоречит, ибо те соображения, которыми мы при этом пользовались (релятивистская кинематика, принцип относительности, законы соударений упругих тел), основаны в конце концов на опыте. Из них еще не вытекает, что закон сохранения импульса в такой формулировке будет выполняться всегда и всюду; эта гипотеза, будучи чрезвычайно правдоподобной, нуждается в подтверждении на опыте. Некоторые результаты опытов мы рассмотрим ниже; сейчас же мы можем сказать, что закон сохранения релятивистского импульса подтвержден огромным экспериментальным материалом и в настоящее время по праву может считаться твердо установленным физическим фактом.
Обратимся теперь к вопросу о массе. С первого взгляда представляется, что вопрос этот уже решен,— мы обозначили массу через т0 и без дальнейших околичностей ввели эту величину в формулу релятивистского импульса; при этом считалось само собой разумеющимся, что масса не зависит от скорости, т. е. является величиной абсолютной. Однако более внимательное рассмотрение показывает, что дело обстоит тут не так просто.
Обратимся сначала еще раз к нашей ускоренно движущейся ракете. По мере роста ее скорости дальнейшее ее ускорение происходит все медленнее; прибавить к уже имеющейся скорости одну и ту же «добавку» становится все труднее. Чем больше скорость ракеты, тем больше она «сопротивляется» попыткам дальнейшего изменения скорости. В некотором смысле инертность тела возрастает вместе с ростом его скорости. Но ведь мерой инертности является масса. Нужно признать, следовательно, что по мере увеличения скорости масса тела должна возрастать. Величина т0 остается, конечно, постоянной; наши рассуждения показывают лишь, что свойства инертности тела характеризуются этой величиной далеко не полностью.
Теперь обратим внимание еще на один чрезвычайно важный физический закон, тесно связанный с законом сохранения импульса, так называемый закон движения центра тяжести. Он заключается, как известно, в том, что одними лишь внутренними силами нельзя изменить движения центра тяжести системы тел. Если на любую сколь угодно сложную систему внешние силы не действуют, то центр тяжести ее будет двигаться равномерно и прямолинейно. В частности, для такой системы всегда можно выбрать такую систему отсчета, в которой центр тяжести будет неподвижен, каким бы сложным ни
было движение отдельных тел. Рассмотрим этот закон с точки зрения теории относительности.
Пусть имеются два тела с массами m0 и М0; пусть они вначале неподвижны и соприкасаются друг с другом. Их общий центр тяжести будет находиться близ точки соприкосновения. Пусть, далее, в некоторый момент времени эти тела внезапно друг от друга отталкиваются. Для определенности можно представить себе, что это отталкивание производится с помощью сжатой пружины, которая в нужный момент освобождается. В результате оба тела получат одинаковые по величине импульсы (так как до отталкивания их общий импульс был равен нулю), но так как массы их различны, то различны будут и скорости; обозначим абсолютные величины скоростей через u и U. Через единицу времени после момента отталкивания наши тела будут находиться от прежнего положения центра тяжести на расстояниях, равных как раз u и U (рис. 29).
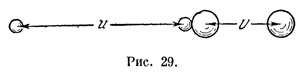 |
Известно, что центр тяжести двух тел находится на прямой, соединяющей эти тела, ближе к телу с большей массой, и притом во столько раз, во сколько раз больше масса. Так как до начала движения центр тяжести был неподвижен, он должен находиться в той же самой точке и теперь. Таким образом, должно, казалось бы, выполняться соотношение
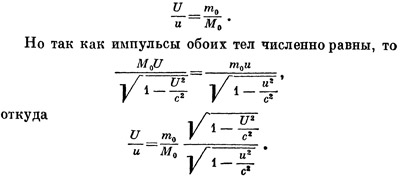
Это значит, что, вычисляя положение центра тяжести системы движущихся тел, мы должны брать вместо
m0 и Мо величины
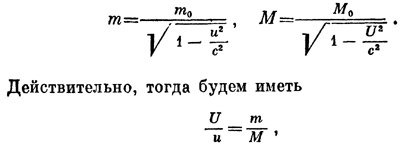
в соответствии с обычным правилом вычисления центра тяжести.
Стало быть, наряду с «обычной» массой, которую мы обозначили через т0, в теории относительности играет роль также и величина, обозначенная нами через т. Если скорость тела относительно невелика, эти две величины практически совпадают, но при больших скоростях т растет и может стать сколь угодно большой. Вспомнив нашу ракету, мы приходим к заключению, что величина т отражает свойства инертности тела гораздо полнее, чем т0.
Но продолжим наши рассмотрения. Представим себе прямоугольный ящик с абсолютно упругими стенками; пусть его масса будет М0. Эту массу мы можем измерить, действуя на ящик внешней силой известной величины и измеряя полученное им ускорение. При этом можно ограничиться малыми силами и ускорениями, так что в результаты измерений релятивистских поправок можно не вносить.
Допустим теперь, что к этому ящику приближается релятивистская, т. е. очень быстро движущаяся, частица с массой т0. В тот момент, когда она подойдет вплотную, откроем одну из стенок ящика, пропустив внутрь частицу, а затем тотчас же закроем стенку, так что наша частица окажется «запертой». Поскольку стенки ящика абсолютно упруги, частица начнет «метаться» по ящику из конца в конец, ударяясь о его стенки. Рассматривая ящик снаружи, мы обнаружим, что под действием ударов частицы он «дрожит». Если скорость частицы достаточно велика, то эта дрожь будет столь частой, что мы можем считать ящик всреднем неподвижным (или движущимся равномерно и прямолинейно).
Попытаемся теперь снова измерить массу ящика. Для этого подействуем на него той же самой силой и измерим ускорение, которое он при этом получит. Находящаяся внутри частица будет также принимать участие в движении ящика, так что сообщенная ящику скорость прибавится к той быстропеременной скорости, какой обладает частица внутри ящика (разумеется, при таком сложении скоростей необходимо учитывать их мгновенные направления). Но мы уже видели, что изменить скорость быстро движущегося тела труднее, чем неподвижного или движущегося медленно. Поэтому наша частица будет сопротивляться изменению скорости тем сильнее, чем больше ее собственная скорость. Это вполне подтверждается точным расчетом, основанным ца законе сохранения импульса. Оказывается, что при повторном измерении массы мы получим результат, который больше старого как раз на величину т! Стало быть, новая видимая масса ящика с запертой в нем частицей складывается из массы самого ящика и величины т частицы.
Тем самым значение этой величины т еще больше возрастает; пора присвоить ей название. Ее называют релятивистской массой. Так как при u=0 имеем m=т0, то величину т0 называют массой покоя.
Мы можем рассмотреть ящик, в котором заперты не одна, а много частиц. Результат будет тем же самым — видимая масса ящика равна массе пустого ящика плюс сумма релятивистских масс всех находящихся в нем частиц. Но такой ящик представляет собой не что иное, как простейшую модель сосуда, наполненного газом. Значит, общая масса такого сосуда складывается из массы его стенок и релятивистских масс молекул газа. То же самое относится и к твердому телу, так как его молекулы совершают, как известно, беспрерывное тепловое движение. Измеряя массу твердого тела, мы измеряем, собственно, суммарную релятивистскую массу всех его молекул. Стало быть, рассматриваемая нами видимая масса есть просто та самая масса, которая служит мерой инертности тела. Если тело неподвижно, то она равна массе покоя, если же тело движется, то это будет его релятивистская масса.
Если два или несколько тел соединяются, образуя одно новое тело, то релятивистская масса нового тела будет в точности равна сумме релятивистских масс составных его частей; таким образом, релятивистская масса подчиняется закону сохранения. Что же касается массы покоя, то для нее никакого закона сохранения не существует. В самом деле, на примере сосуда с газом мы видели, что его масса покоя отнюдь не равна сумме масс покоя молекул и стенок. Более того, мы скоро убедимся, что масса покоя может уничтожаться или возникать там, где раньше никакой такой массы не было.
Итак, релятивистский закон сохранения массы формулируется точно так же, как и классический; отличие состоит лишь в том, что вместо классической массы (которую до некоторой степени можно отождествить с массой покоя) в него входит масса релятивистская. Поскольку эта масса является величиной относительной, то и новый закон по своему значению и физическому содержанию существенно отличается от классического закона.
Раньше полагали, что можно измерить массу сколь угодно сложной физической системы, измеряя поочередно массы ее составных частей; при этом можно было составные части вынимать из системы, водворяя их на прежнее место после измерений. Считалось, что арифметическая сумма полученных таким образом масс и есть масса всей системы. Закон сохранения массы считался законом статическим, движение и внутреннее состояние системы не имело к нему никакого отношения.
Теория относительности такой процедуры уже не допускает. Масса тела не равна простой сумме масс покоя его составных частей; здесь необходим учет движения и взаимодействия их между собой. Закон сохранения массы утратил свою статичность, он стал законом динамическим, законом движения. Правильнее всего его было бы формулировать следующим образом: в любой (изолированной от внешних воздействий) физической системе составляющие ее тела движутся таким образом, что их суммарная релятивистская масса остается постоянной.
Некоторая парадоксальность этого закона связана, конечно, с тем, что релятивистская масса есть величина относительная, т. е. зависит от выбора системы отсчета. Все мы со школьной скамьи слишком привыкли видеть в массе не столько меру инертности, сколько меру количества вещества или материи; зачастую само слово «масса» фигурирует в качестве синонима «материи». Трудно отрешиться от мысли, что если масса тела меняется, то с ним обязательно что-то должно происходить, как-то должно меняться и внутреннее состояние тела. Безусловно, масса обладает многими свойствами, делающими ее подходящим средством для измерения количества вещества. Это связано в первую очередь с тем, что при обычных скоростях релятивистская масса практически точно совпадает с массой покоя, а физические явления, связанные с «исчезновением» и «зарождением» массы покоя, дают слишком ничтожный эффект. Поэтому и получается, что масса тела практически равна сумме масс его составных частей. Как видим, более точный учет релятивистских эффектов показывает, что эти представления являются лишь некоторым приближением к действительности.
Но не указывает ли закон сохранения релятивистской массы на то, что эта масса все же может служить мерой количества материи? Ведь известно, что материя не уничтожается и не самозарождается. Даже в тех случаях, когда пропадает масса покоя, материя отнюдь не пропадает; она лишь переходит в другую форму.
Такому пониманию релятивистской массы препятствует опять-таки ее относительность. Одно и то же тело в различных системах отсчета имеет различную массу; выходит, что в различных системах отсчета в нем содержится различное количество материи. Но если даже примириться с этим, все же никак нельзя избежать нелепостей. Рассмотрим, например, два упругих шара одинаковой массы покоя. Пусть первый шар движется, а второй неподвижен. Известно, что возможно такое их столкновение, после которого первый шар остановится, а второй будет двигаться с той же скоростью в том же направлении. До столкновения большую релятивистскую массу имеет первый шар; после столкновения, наоборот, большей массой обладает другой. Мы вынуждены заключить, что в момент удара часть материи первого шара каким-то образом перешла на второй шар. Рассмотрим теперь то же самое движение в системе отсчета, где до удара неподвижен не второй, а первый шар. Там все происходит в обратном порядке: большую массу имеет сначала второй шар, а потом первый. Получается, что материя перешла со второго шара на первый. Все это делает весьма и весьма сомнительной пользу рассмотрения массы как количества материи.
Масса не есть материя, а лишь одно из свойств материи. Закон сохранения массы не есть закон сохранения материи. Безусловно, сохранение массы в какой-то степени отражает факт сохранения материи; но считать этот физический закон точным и адекватным количественным выражением общефилософского принципа сохранения материи было бы ошибкой.
Свойство инертности материи в классической физике описывалось одной величиной; теория относительности выявила большее богатство, разносторонность этого понятия. Одной величины для отображения этого свойства оказывается недостаточно, теперь приходится иметь дело с двумя величинами — относительной и абсолютной.
Теперь рассмотрим несколько детальнее вопрос о преобразовании массы и импульса при изменении системы отсчета. Мы знаем, как эти величины выражаются через массу покоя и скорость; при перемене системы отсчета масса покоя не меняется, а скорость преобразуется согласно релятивистскому закону сложения скоростей. Таким образом, зная массу и импульс тела в одной системе отсчета, мы всегда сможем вычислить их в любой другой системе. Если в системе отсчета S
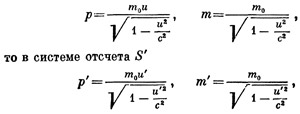

Результат этот весьма интересен. Мы получили, что при перемене системы отсчета импульс и масса преобразуются так же, как и координаты событий, по формулам Лоренца. Это значит, что между массой и импульсом существует такая же связь, как и между пространством и временем: как та, так и другая пара величин объединяются в некоторую сложную величину. Тем самым и законы сохранения массы и импульса соединяются в единый закон сохранения новой сложной величины — массы — импульса.
Установленный нами закон преобразования массы и импульса на математическом языке означает, что масса и импульс вместе составляют единый четырехмерный вектор. То, что мы имели дело лишь с двумя измерениями, вызвано, конечно, нашим рассмотрением только одномерных задач. Вообще же импульс есть, как известно, величина векторная, т. е. имеет три компоненты. Теория относительности прибавляет еще одну — релятивистскую массу.
Объединение ранее разнородных и даже независимых понятий в единое целое является вообще характерной особенностью теории относительности. Особенно важным успехом ее в этом направлении является теория электромагнитного поля. Классическая теория, созданная трудами Максвелла и Лоренца, страдала многими характерными недостатками. Известно, например, что при вдвигании магнита внутрь проволочной катушки в ней возникает электрический ток. Это явление объясняется законом индукции Фарадея. Наоборот, если катушку надвигать на неподвижный магнит, то появляющийся в ней ток относится за счет действия так называемых сил Лоренца. Хотя с точки зрения принципа относительности перед нами совершенно одно и то же явление, объяснение его в обоих случаях совершенно различно! То обстоятельство, что как в том, так и в другом случае сила тока получается одинаковой, выглядит чистейшей случайностью.
Это значит, что теория Максвелла — Лоренца не совсем удовлетворяет принципу относительности; как мы знаем, это и явилось основной побудительной причиной к созданию теории относительности. В своей первой работе Эйнштейн занимается в первую очередь приведением законов электродинамики в соответствие с принципом относительности. Достигается это прежде всего объединением электрического и магнитного поля в единое новое понятие — электромагнитное поле. Если раньше в теории фигурировало два вектора, напряженности электрического и магнитного ноля, то теперь в ней появилось одно сложное математическое понятие, так называемый тензор электромагнитного поля. При перемене системы отсчета компоненты этого тензора преобразуются по формулам преобразования Лоренца. Формулы преобразований показывают, в частности, что если в некоторой системе отсчета поле является чисто магнитным, то в другой системе у него появляются и электрические составляющие. Таким образом, в случае катушки и магнита в той системе отсчета, где катушка неподвижна, в обоих случаях существует электрическое поле, которое и вызывает ток. Так устраняется упомянутая выше «неувязка». Кроме того, новая теория позволяет легко и просто решать многие задачи, которые раньше вызывали серьезные затруднения. Например, поле движущегося заряда определяется простым изменением системы отсчета, так как поле заряда неподвижного хорошо известно — оно дается законом Кулона.
Рассмотрим еще вкратце вопрос о силе в релятивистской механике. Мы уже упоминали, что силой можно было бы назвать произведение «собственного» ускорения тела на его массу покоя. Однако по ряду причин такое определение неудобно. В теории относительности силу определяют как произведение собственного ускорения на релятивистскую массу. Тогда второй закон Ньютона записывается в таком виде:
p2 - p1 = f(τ2 - τ1)
Таким образом, словесная его формулировка почти не изменяется: изменение импульса равно произведению силы на соответствующий промежуток собственного времени данного тела.
Так как релятивистская масса растет вместе со скоростью, то даже в случае равноускоренного движения действующая на тело сила увеличивается; так обстоит дело и с неоднократно рассматривавшейся выше ракетой. Нужно сказать, что в теории относительности все силы, как правило, зависят от скорости тела, на которое они действуют. Это имеет место, в частности, и при движении заряженного тела в постоянном и однородном электрическом поле. Кстати, в этом случае движение будет как раз равноускоренным.
В связи с определением силы у читателя может возникнуть недоумение. Ведь, казалось бы, сила есть некоторое объективное отношение между телами и полями, существующее совершенно независимо от какой бы то ни было теории. Как же в таком случае можно выбирать определение силы? Должно бы существовать одно-единственное определение — то, которое отвечает действительности, а не удобству.
Дело здесь в том, что, определяя силу как произведение массы на ускорение, мы имеем в виду не саму силу, как объективное взаимодействие между реальными физическими телами, а лишь число, с помощью которого мы эту силу измеряем и которое будет подставляться в соответствующие уравнения. Способы же измерения силы могут быть различными. Если бы мы пожелали измерять силу, например, произведением массы покоя на ускорение, то второй закон Ньютона принял бы вид
p2 - p1 = f(t2 - t1)
Хотя обе формулировки этого закона и различны по форме, они выражают одно и то же физическое содержание. Решая одну и ту же задачу с помощью обоих уравнений, мы получим один и тот же ответ (разумеется, вместо f в каждом случае будут подставляться различные числа).
Признать то или иное определение правильным или неправильным, удачным или неудачным можно лишь в процессе развития всей теории, которая на каждом шагу непрерывно сравнивается с опытом. Формальных признаков для такого отбора не существует; с формальной точки зрения всякое определение до некоторой степени произвольно и выглядит как некое условное соглашение. Действительный смысл и значение каждого научного понятия нельзя оценить, прочтя только первые страницы соответствующей монографии, где дается определение этому понятию; это можно сделать после усвоения всей теории или хотя бы достаточно значительной ее части. В настоящей книге мы, понятно, лишены такой возможности»
Отметим в заключение, что релятивистские формулы импульса и массы были подвергнуты опытной проверке даже еще до создания теории относительности. В начале текущего столетия физиками были предприняты первые успешные попытки измерения заряда и массы элементарной частицы материи — электрона. С этой целью поток свободных электронов пропускался через электромагнитное поле, которое, действуя на электроны, заставляло их отклоняться от прямолинейного пути. Зная величину этого отклонения, можно было вычислить скорость электрона, а также отношение его электрического заряда, к массе. Опыты с очень быстрыми электронами показали, что отношение заряда к массе с ростом скорости уменьшается. Так как на основании весьма веских соображений заряд электрона от его скорости зависеть не может, остается допустить, что по мере возрастания скорости увеличивается масса. Первые опыты давали невысокую точность и лишь качественно подтвердили формулу для массы, данную Лоренцом (эта формула совпадает с известной нам релятивистской формулой).
Нужно сказать, что в то время с формулой Лоренца конкурировала другая, выведенная из других соображений Абрагамом. Вскоре появилась на свет теория относительности, и вопрос о выборе той или другой формулы приобрел принципиальное значение. Последовал целый ряд теоретических и экспериментальных работ; возникла полемика. Однако первые убедительные экспериментальные результаты в пользу формулы Лоренца — Эйнштейна удалось получить лишь в двадцатых годах.
В настоящее время формула Абрагама имеет лишь исторический интерес.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 Можно ли без всяких изменений перенести все эти законы и соотношения в.теорию относительности? Другими словами, совместимы ли они с релятивистской кинематикой? Легко убедиться, что ответ на этот вопрос будет отрицательным. В самом деле, рассмотрим хотя бы следующий простой пример.
Можно ли без всяких изменений перенести все эти законы и соотношения в.теорию относительности? Другими словами, совместимы ли они с релятивистской кинематикой? Легко убедиться, что ответ на этот вопрос будет отрицательным. В самом деле, рассмотрим хотя бы следующий простой пример.