| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Волны в плотных материалах
Прежде всего я напомню вам об удобном способе описания синусоидальных плоских волн, которым мы пользовались в гл. 36 (вып. 3). Любая компонента поля в волне (возьмем, например, Е) может быть записана в форме
где Е — амплитуда поля в точке r (относительно начала координат) в момент t. Вектор k указывает направление распространения волны, а его величина |k|= k=2π/λ равна волновому числу. Фазовая скорость волны vфаз=ω/k для света в материале с показателем n будет равна с/n, поэтому
где кх, кy и kz — компоненты вектора k по трем осям. Мы уже отмечали однажды, что на самом деле величины (ω, кх, кy , kz) образуют четырехвектор и что его скалярное произведение на (t, х, у, z) является инвариантом. Таким образом, фаза волны есть инвариант и формулу (33.6) можно записать в виде
Однако сейчас нам такие хитрости не понадобятся.
Правило остается справедливым для операции V в любой комбинации, будь то градиент, дивергенция или ротор. Например, z-компонента V хЕ равна
Если и Еy и Ех изменяются как e–¡ k·r, то мы получаем
что представляет, как вы видите, z-компоненту –¡kxE.
Это соответствует результату, найденному ранее для волн в пустом пространстве, т. е. что вектор В в волне направлен под прямым углом к вектору Е и направлению распространения волны. (В пустом пространстве ω/к=с.) Знак в уравнении (33.9) вы можете проверить, исходя из того, что k является направлением вектора Пойнтинга S=ε0c2(ExB).
Поскольку вектор k перпендикулярен оси z, то
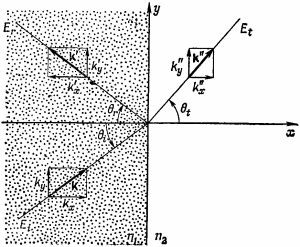
Отраженную волну мы запишем как
так что ее частота равна ω′, волновое число k′, а амплитуда Е′0. (Мы, конечно, знаем, что частота и величина вектора k в отраженной волне те же, что и в падающей волне, но не хотим предполагать даже это. Пусть это все получится само собой из математического аппарата.) Наконец, запишем преломленную волну:
Вы знаете, что одно из уравнений Максвелла дает соотношение (33.9), так что для каждой из волн
Кроме того, если показатели преломления двух сред мы обозначим через n1 и n2, то из уравнения (33.10) получится
Поскольку отраженная волна находится в том же материале, то
в то время как для преломленной волны
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.



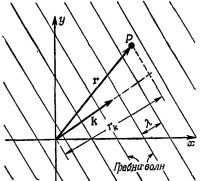 Предположим, что вектор k направлен по оси z; тогда к·r будет просто хорошо знакомым нам kz. Для вектора k в любом другом направлении z следует заменить на rk — расстояние от начала в направлении вектора к, т. е. kz мы должны заменить на krk, что как раз равно к·r (фиг. 33.2). Таким образом, запись (33.6) является удобным представлением волны, идущей в любом направлении.
Предположим, что вектор k направлен по оси z; тогда к·r будет просто хорошо знакомым нам kz. Для вектора k в любом другом направлении z следует заменить на rk — расстояние от начала в направлении вектора к, т. е. kz мы должны заменить на krk, что как раз равно к·r (фиг. 33.2). Таким образом, запись (33.6) является удобным представлением волны, идущей в любом направлении.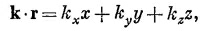
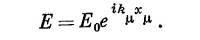
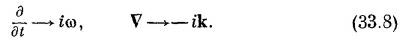
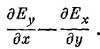
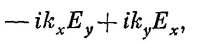
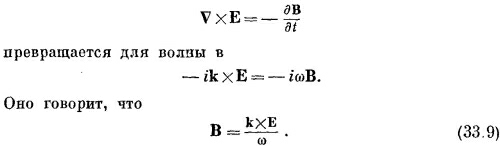

 Но раз уже это известно нам, давайте не будем проделывать все сначала.
Но раз уже это известно нам, давайте не будем проделывать все сначала.