Главная >> Фейнмановские лекции по физике >> Том 7 >> Глава 34. Магнетизм вещества

Магнитная энергия атомов

Теперь я снова хочу поговорить о магнитном моменте. Я уже говорил, что в квантовой механике магнитный момент атомной системы может быть связан с моментом количества движения  соотношением   (34.6):

где  —q_e—заряд,   а   т — масса   электрона.
 
Атомные магнитики, будучи помещены во внешнее магнитное поле, приобретут дополнительную магнитную энергию, которая зависит от компоненты их магнитного момента в направлении поля.  Мы знаем, что

Выбирая ось z вдоль направления поля В, получаем

А используя уравнение (34.27), находим

Согласно квантовой механике, величина J_z может принимать только такие значения: jh, (j—1)h,...,– jh. Поэтому магнитная энергия атомной системы не произвольна, допустимы только некоторые ее значения. Например, максимальная величина энергии   равна

Величину q_eh/2m обычно называют «магнетоном Бора» и обозначают   через   μ_B:

Возможные значения магнитной энергии будут следующими:

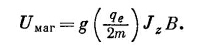
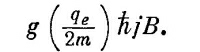
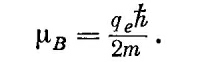
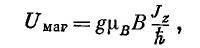
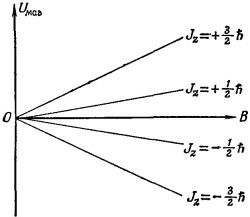где J_z/h принимает одно из следующих значений: j, (j–1), (j–2),    ...,   (–j+1),    –j.
 
Другими словами, энергия атомной системы, помещенной в магнитное поле, изменяется на величину, пропорциональную полю и компоненте J_z. Мы говорим, что энергия атомной магнитной системы «расщепляется магнитным полем на 2j+1 уровня». Например, атомы со спином j=³/₂, энергия которых вне магнитного поля равна U₀, в магнитном поле будут иметь четыре возможных значения энергии. Эти энергии можно изобразить на диаграмме энергетических уровней наподобие фиг. 34.5. Однако энергия каждого атома в данном поле В принимает только одно из четырех возможных значений. Именно это говорит квантовая механика о поведении атомной системы в магнитном поле.

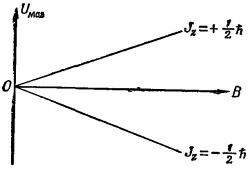Простейшая «атомная» система — отдельный электрон. Спин электрона равен ¹/₂ , поэтому у него возможны два состояния: J_z = h/2 и J_z=–h/2. Для спинового магнитного момента отдельного покоящегося электрона (у которого отсутствует орбитальное движение) g=2, так что магнитная энергия будет ±μ_BB. На фиг. 34.6 показаны возможные энергии электрона в магнитном поле. Грубо говоря, спин электрона направлен либо «вверх» (по магнитному полю), либо «вниз» (против поля).
 
У системы с более высоким спином число состояний тоже больше. Поэтому мы можем в зависимости от величины J_z говорить о спине, направленном «вверх» или «вниз» или под некоторым  «углом».
 
Эти результаты квантовой механики мы будем использовать при обсуждении магнитных свойств материалов в следующей главе.

СМОТРИТЕ ТАКЖЕ: