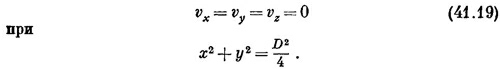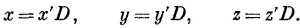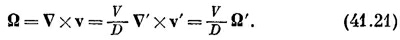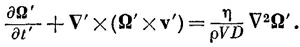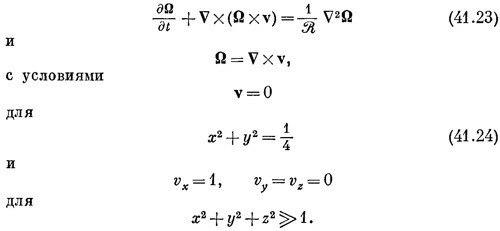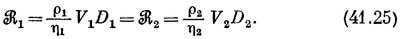Главная >> Фейнмановские лекции по физике >> Том 7 >> Глава 41. Течение «мокрой» воды

Число Рейнольдса

Посмотрим теперь, как изменяется течение жидкости из-за нового члена с вязкостью. Рассмотрим несколько подробнее две задачи. Первая — обтекание жидкостью цилиндра; эту задачу мы пытались решить в предыдущей главе, используя теорию невязкой жидкости. Оказывается, что сегодня возможно найти решение вязких уравнений только для некоторых специальных случаев. Так что кое-что из того, что я расскажу вам, основано на экспериментальных измерениях, считая, конечно, что экспериментальная модель удовлетворяла уравнению  (41.17).
 
Математически задача состоит в следующем: мы хотим найти решение для потока несжимаемой вязкой жидкости вблизи длинного цилиндра диаметром D. Поток должен определяться уравнением (41.17) и

с условием, что скорость на больших расстояниях равна некоторой постоянной V (параллельной оси х), а на поверхности цилиндра равна нулю. Так что

Это полностью определяет математическую задачу.
 
Если вы вглядитесь в эти выражения, то увидите, что в задаче есть четыре различных параметра: η, ρ, D и V. Можно подумать, что нам придется иметь дело с целой серией решений для разных V, разных D и т. д. Вовсе нет. Все возможные различные решения соответствуют разным значениям одного параметра. Такова наиболее важная общая вещь, которую мы можем сказать о вязком потоке. А чтобы понять, почему это так, заметьте сначала, что вязкость и плотность появляются в виде отношения η/ρ, т. е. удельной вязкости. Это уменьшает число независимых параметров до трех. Предположим теперь, что все расстояния мы измеряем в единицах той единственной длины, которая появляется в задаче: диаметра цилиндра D, т. е. вместо х, у, z мы вводим новые переменные х′, у′, z′, причем

При этом параметр D из (41.19) исчезает. Точно так же если будем измерять все скорости в единицах V, т. е. если мы положим v = v′V, то избавимся от V, a v′ на больших расстояниях будет просто равно единице. Поскольку мы фиксировали наши единицы длины и скорости, то единицей времени теперь должно быть D/V, так что мы должны сделать подстановку:

В наших новых переменных производные в уравнении (41.18) тоже изменятся: так, д/дх перейдет в (1/D) (д/дх′) и т. д., так что уравнение (41.18) превратится в

А наше основное уравнение (41.17) перейдет в

Все постоянные при этом  собираются в один множитель, который мы, следуя традиции, обозначим через 1/R:

Если теперь  мы  просто запомним,  что все наши уравнения должны выписываться для величин, измеряемых в новых единицах, то все штрихи  можно опустить. Тогда уравнения для потока примут вид

Что все это значит? Если, например, мы решили задачу для потока с одной скоростью V₁ и некоторого цилиндра диаметром D₁, а затем интересуемся обтеканием цилиндра другого диаметра D₂ другой жидкостью, то поток будет одним и тем же при такой скорости V₂, которая отвечает тому же самому числу Рейнольдса, т. е. когда

В любых случаях, когда числа Рейнольдса одинаковы, поток при выборе надлежащего масштаба х′, у′, z′ и t′ будет «выглядеть» одинаково. Это очень важное утверждение, ибо оно означает, что мы можем определить поведение потока воздуха при обтекании крыла самолета, не строя самого самолета и не испытывая его. Вместо этого мы можем сделать модель и провести измерения, используя скорость, которая дает то же самое число Рейнольдса. Именно этот принцип позволяет нам применять результаты измерений над маленькой моделью самолета в аэродинамической трубе или результаты, полученные с моделью корабля, к настоящим объектам. Напомню, однако, что это можно делать только при условии, что сжимаемостью жидкости можно пренебречь. В противном случае войдет новая величина — скорость звука. При этом различные модели будут действительно соответствовать друг другу только тогда, когда отношение V к скорости звука тоже приблизительно одинаково. Отношение скорости V к скорости звука называется числом Маха. Таким образом, для скоростей, близких к скорости звука или больших, поток в двух задачах будет выглядеть одинаково, если и число Маха и число Рейнольдса в обеих ситуациях одинаковы.

СМОТРИТЕ ТАКЖЕ: