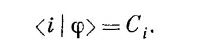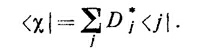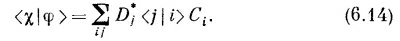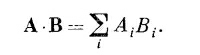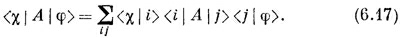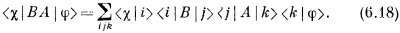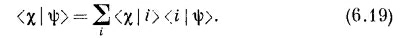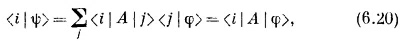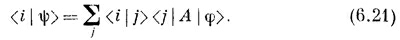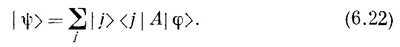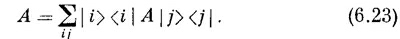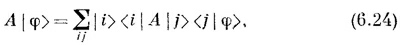Главная >> Фейнмановские лекции по физике >> Том 8 >> Глава 6. Гамильтонова матрица

Разложение векторов состояний

Посмотрим на уравнение (6.8) еще раз; его можно рассматривать следующим образом. Любой вектор состояния |φ> может быть представлен в виде линейной комбинации совокупности базисных «векторов» с подходящими коэффициентами, или, если угодно, в виде суперпозиции «единичных векторов» в подходящих пропорциях. Чтобы подчеркнуть, что коэффициенты <¡ |φ> — это просто обычные (комплексные) числа, напишем

Тогда (6.8) совпадает с

Такое же уравнение можно написать и для всякого другого вектора состояния, скажем для |x>, но, конечно, с другими коэффициентами, скажем с D_¡. Тогда будем иметь

где D_¡ — это просто амплитуды <i |x>.
 
Представим, что мы начали бы с того, что в (6.1) абстрагировались бы от φ. Тогда мы бы имели

Вспоминая,  что  <x | ¡> = <¡ | x> ,  можно записать это в виде

А теперь интересно вот что: чтобы обратно получить <x| φ>, можно просто перемножить (6.13) и (6.10). Только, делая это, надо быть внимательным к индексам суммирования, потому  что они  в разных  уравнениях разные. Перепишем сперва (6.13):

Это ничего не меняет. Объединяя с (6.10), получаем

Вспомните, однако, что <j |¡> = δ_¡j, так что в сумме останутся только члены с j=i. Выйдет

где, как вы помните, D_¡ = <¡ | х>  = <x | ¡> а С_i = <¡ I φ>. Опять мы являемся свидетелями тесной аналогии со скалярным произведением

Единственная разница — что D_¡ нужно комплексно сопрягать. Значит, (6.15) утверждает, что если разложить векторы состояний <x | и φ> по базисным векторам < i | или | i >, то амплитуда перехода из φ в x дается своего рода скалярным произведением (6.15). А это просто (6.1), записанное в других символах. Мы ходим по кругу, привыкая к новым символам.
 
Может быть, стоит подчеркнуть, что в то время, как пространственные трехмерные векторы выражаются через три ортогональных единичных вектора, базисные векторы | i > квантовомеханических состояния должны пробегать всю совокупность, отвечающую данной задаче. В зависимости от положения вещей в нее может входить два или три, пять или бесконечно много  базисных состояний.
 
Мы говорили также о том, что происходит, когда частицы проходят через прибор. Если мы выпустим частицы в определенном состоянии φ, затем проведем их через прибор, а после проделаем измерение, чтобы посмотреть, находятся ли они в состоянии х, то результат будет описываться амплитудой

Такой символ не имеет близкого аналога в векторной алгебре. (Он ближе к тензорной алгебре, но эта аналогия не так уж полезна.) Мы видели в гл. 3 [формула (3.32)], что (6.16) можно переписать так:

Это пример двукратного применения основного правила (6.9).
 
Мы обнаружили также, что если вслед за прибором А поставить другой прибор  B,  то можно написать

Это опять-таки следует прямо из предложенного Дираком метода записи уравнения (6.9). Вспомните, что между В и А всегда можно поставить черту (|), которая ведет себя совсем как множитель единица.
 
Кстати говоря, об уравнении (6.17) можно рассуждать и иначе. Предположим, что мы рассуждаем о частице, попадающей в прибор А в состоянии φ и выходящей из него в состоянии ψ. Мы можем задать себе такой вопрос: можно ли найти такое состояние ψ, чтобы амплитуда перехода от ψ к x тождественно совпадала с амплитудой <х|A|φ>? Ответ гласит: да. Мы хотим, чтобы (6.17) заменилось уравнением

Конечно, этого ложно достичь, если взять

что и определяет собой ψ. «Но оно не определяет собой ψ, — скажете вы,— оно определяет только <i |ψ>. Однако <i |ψ> все же определяет ψ; ведь если у вас есть все коэффициенты, связывающие ψ с базисными состояниями ¡, то ψ определяется однозначно. И действительно, можно поупражняться с нашими обозначениями и записать (6.20) в виде

А раз  это  уравнение справедливо при  всех  ¡,  то  можно просто писать

Теперь мы вправе сказать: «Состояние ψ — это то, что получается, если начать с φ и пройти сквозь аппарат А».
 
Еще один, последний пример полезных уловок. Начинаем опять с (6.17). Раз это уравнение соблюдается при любых x и φ, то их обоих  можно сократить! Получаем

Что это значит? Только то, что получится, если вернуть на свои места φ и x. В таком виде это уравнение «недокончено» и неполно. Если умножить его «справа» на |φ>, то оно превращается  в

а это снова то же уравнение (6.22). В самом деле, мы бы могли просто убрать из (6.22) все j и написать

Символ А — это не амплитуда и не вектор; это вещь особого рода, именуемая оператором. Он — нечто, что «оперирует» над состоянием, чтобы создать новое состояние; уравнение (6.25) говорит, что |ψ> — это то, что получается, если А действует на |φ>. Это уравнение тоже нужно считать недоконченным, открытым, пока слева оно не умножится на какое-то «брэ», скажем на   <x |, и не обратится в

Оператор А, разумеется, полностью описывается тем, что задается матрица амплитуд <i |Al j>; ее также пишут в виде A_¡j— через любую совокупность базисных векторов.
 
Все эти математические обозначения на самом деле ничего нового не вносят. Единственный резон, почему мы их ввели,— мы хотели показать, как пишутся обрывки уравнений, потому что во многих книжках вы встретите уравнения, написанные в неполном виде, и нет причин вам пугаться, увидев их. Если вы захотите, вы всегда сможете дописать те части, которых не хватает, и получить уравнение, связывающее числа. Оно будет выглядеть  более привычно.
 
Кроме того, как вы увидите, обозначения «брэ» и «кет» очень удобны. Прежде всего мы теперь сможем указывать состояния, задавая их вектор состояния. Когда мы захотим вести речь о состоянии с определенным импульсом р, то скажем: «состояние |р>». Или будем говорить о некотором произвольном состоянии |ψ>. Для единообразия мы всегда, говоря о состоянии, будем употреблять «кет» и писать |ψ>. (Конечно, этот выбор совершенно произволен; в равной мере мы могли бы остановиться и на «брэ»  <ψ|.)

СМОТРИТЕ ТАКЖЕ: