Главная >> Фейнмановские лекции по физике >> Том 8 >> Глава 7. Аммиачный мазер

Переходы вне резонанса

Наконец, хотелось бы выяснить, как изменяются состояния в условиях, когда частота полости, хотя и близка к ω₀, но не совпадает с ней. Эту задачу можно было бы решить точно, но мы не будем пытаться это делать, а обратимся к важному случаю малого электрического поля и малого промежутка времени T, так что μE₀T/h много меньше единицы.Тогда даже в случае уже изученного нами идеального резонанса вероятность перехода очень мала. Будем исходить опять из того, что γ_I =1 и γ_II =0. Тогда мы вправе ожидать, что в течение всего времени Т наша величина γ_I останется близкой к единице, а γ_II будет малой по сравнению с единицей, и задача облегчается. Из второго уравнения (7.45) мы можем подсчитать γ_II принимая γ_I равной  единице и  интегрируя от t=0 до   t=T.   Получается

Это та величина γ_II, которая стоит в (7.40), и она дает амплитуду того, что переход из состояния |/> в состояние |II> произойдет за время Т. Вероятность Р (/→II) такого перехода равна |γ_II|², или

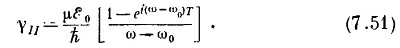
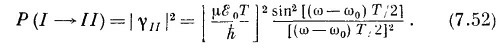
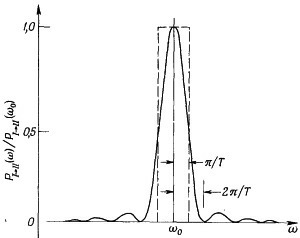Интересно начертить эту вероятность при фиксированном времени Т как функцию частоты полости, чтобы посмотреть, насколько чувствительна она к частотам близ резонансной частоты ω₀. Кривая Р (I →II) показана на фиг. 7.7. (Вертикальная шкала была подогнана так, чтобы в пике была единица, для этого разделили на величину вероятности при ω = ω_о.) С подобными кривыми мы встречались в теории дифракции, так что они должны быть вам знакомы. Кривая довольно резко падает до нуля при   (ω—ω_о)=2π/T  и  никогда  при больших отклонениях  частоты снова не достигает заметной  величины. Почти вся площадь под кривой лежит в пределах ±π/T. Можно показать [с помощью формулы  _-∞ ∫^∞  (sin²x/x²)dx =π], что  площадь под кривой равна 2π/Т и совпадает с площадью выделенного штрихованной линией прямоугольника.
 
Посмотрим, что это дает для реального мазера. Возьмем разумное время пребывания молекулы аммиака в полости, скажем 1 мсек. Тогда для f₀=24 000 Мгц можно подсчитать, что вероятность падает до нуля при отклонениях (f—f_о)/f₀=1/f₀T т. е. порядка 5·10^-8. Очевидно, что для заметных вероятностей перехода частоты должны очень точно совпадать с ω_о. Этот эффект является основой той большой точности, которой можно достичь в «атомных» часах, работающих на принципе мазера.

СМОТРИТЕ ТАКЖЕ: