| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Рассеяние на нерегулярностях решетки
Теперь мы хотим рассмотреть одиночный электрон в неидеальном кристалле. Наш первоначальный анализ привел к выводу, что у идеальных кристаллов и проводимость идеальна, что электроны могут скользить по кристаллу, как по вакууму, без трения. Одной из самых важных причин, способных прекратить вечное движение электрона, является несовершенство кристалла, какая-то нерегулярность в нем. Допустим, что где-то в кристалле не хватает одного атома, или предположим, что кто-то поставил на место, предназначенное для какого-то атома, совсем не тот атом, какой положено, так что в этом месте все совсем не так, как в прочих местах. Скажем, другая энергия Е0 или другая амплитуда А. Как тогда можно будет описать все происходящее?
Конечно, будут и другие уравнения при |n|>2. Они будут выглядеть так же, как (11.6).
Самое общее решение уравнения (11.6) представляло бы собой сочетание волны вперед и волны назад:
Это решение представляет комплексную волну с амплитудой α, бегущую в направлении +х, и волну с амплитудой β, бегущую в направлении —х.
Физический смысл этого таков: «падающая» волна с амплитудой α приближается к атому «нуль» (или «рассеивателю») слева, а «рассеянная» или «отраженная» волна с амплитудой β бежит обратно, т. е. налево. Не теряя общности, можно положить амплитуду α падающей волны равной единице. Тогда амплитуда β будет, вообще говоря, комплексным числом.
Здесь γ — амплитуда волны, бегущей направо, а δ — амплитуда волны, приходящей справа. Мы хотим рассмотреть такой физический случай, когда вначале волна бежит только слева, и за рассеивателем (или атомом загрязнения) имеется только «прошедшая» волна. Будем поэтому искать решение, в котором δ=0. Стало быть, мы попытаемся удовлетворить всем уравнениям для аn, кроме средней тройки в (11.28), с помощью следующих пробных решений:
Вспомните, что (11.30) выражает Е через k. Подставьте это значение Е в уравнения и учтите, что
Это уравнение сообщает нам, что прошедшая волна (γ) — это просто исходная падающая волна (1) плюс добавочная волна (β), равная отраженной. Это не всегда так, но при рассеянии на одном только атоме оказывается, что это так. Если бы у вас была целая группа атомов примеси, то величина, добавляемая к волне, бегущей вперед, не обязательно вышла бы такой же, как у отраженной волны.
Мы получили полное решение для решетки с одним необычным атомом.
Попробуйте показать, что в нашем решении так оно и есть. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

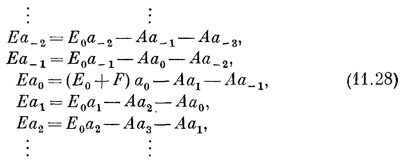
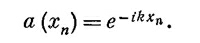
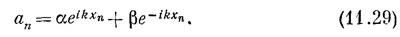
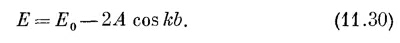
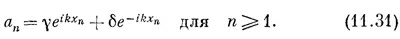
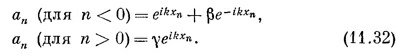
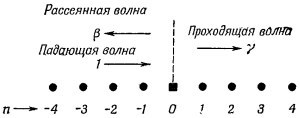 Положение, о котором идет речь, иллюстрируется фиг. 11.6.
Положение, о котором идет речь, иллюстрируется фиг. 11.6.