Главная >> Фейнмановские лекции по физике >> Том 9 >> Глава 11. Распространение в кристаллической решетке

Захват нерегулярностями решетки

Бывает и другой интересный случай. Он может возникнуть, когда F число отрицательное. Если энергия электрона в атоме примеси (при n = 0) ниже, чем где-либо в другом месте, то электрон может оказаться захваченным этим атомом. Иначе говоря, если Е₀ + F ниже самого низа полосы (меньше, чем Е₀—2А), тогда электрон может оказаться «пойманным» в состояние с Е< Е₀—2А. Из всего того, что мы делали до сих пор, такое решение не могло получиться. Но это решение можно получить, если в пробном решении (11.15) разрешить k принимать мнимые значения. Положим k = ix. Для n<0 и для n>0 у нас опять будут разные решения. Для n>0 допустимое решение могло бы иметь вид

В экспоненте мы выбрали плюс; иначе амплитуда при больших отрицательных n стала бы бесконечно большой. Точно так же допустимое решение для n>0 имело бы вид

Если подставить эти пробные решения в (11.28), то они удовлетворят всем уравнениям, кроме средней тройки, при условии, что

А раз сумма этих двух экспонент всегда больше 2, то эта энергия оказывается за пределами (ниже) обычной полосы. Это-то мы и искали. Оставшейся тройке уравнений (11.28) удастся удовлетворить, если взять с = с′ и если x выбрать так, чтобы

Сопоставив это уравнение с (11.41), найдем энергию захваченного электрона

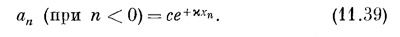
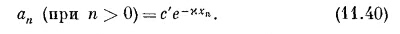
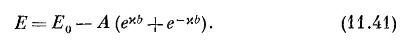
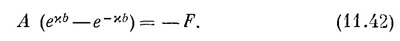
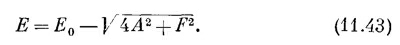
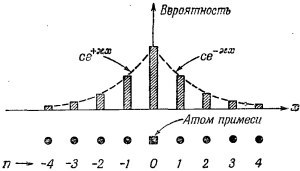Захваченный электрон обладает одной-единственной энергией (а не целой полосой); она расположена несколько ниже полосы проводимости.
 
Заметьте, что амплитуды (11.39) и (11.40) не утверждают, что пойманный электрон сидит прямо в атоме примеси. Вероятность обнаружить его у одного из соседних атомов дается квадратом этих амплитуд. Изменение ее показано столбиками иа фиг. 11.7 (при каком-то наборе параметров). С наибольшей вероятностью электрон можно встретить близ атома примеси. Для соседних атомов вероятность спадает экспоненциально по мере удаления от атома примеси. Это новый пример «проникновения через барьер». С точки зрения классической физики электрону не хватило бы энергии, чтобы удалиться от энергетической «дырки» близ центра захвата. Но квантовомеханически он может  куда-то  недалеко просочиться.

СМОТРИТЕ ТАКЖЕ: