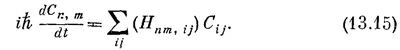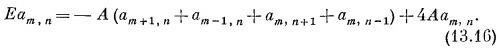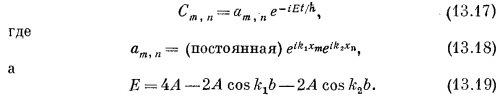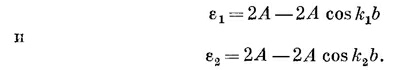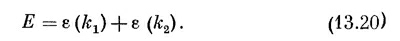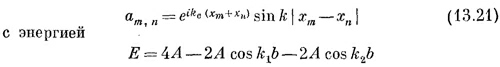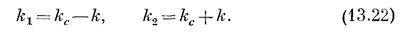| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Две спиновые волны
Пусть нам опять нужно найти стационарные состояния. Как обычно, производные по времени обратятся в Е, умноженное на амплитуду, a Cm,n заменятся коэффициентами ат,n. Затем надо аккуратно рассчитать влияние H на состояние с перевернутыми спинами т и n. Это сделать нетрудно. Представьте на минуту, что т далеко от n, так что не нужно думать, что будет, если ... и т. д. Обменная операция, производимая в точке хn, передвинет перевернутый спин либо к (n + 1)-му, либо к (n — 1)-му атому, так что имеется ненулевая амплитуда того, что теперешнее состояние получилось из состояния | хт, хn+1>, и амплитуда того, что оно произошло из состояния |хт,хn–1>. Но передвинуться мог и второй спин, так что не исключена и какая-то амплитуда того, что Cm,n питается от Сm+1,n или от Cm–1,n. Все эти эффекты должны быть одинаковы. Окончательный вид гамильтонова уравнения для Ст,n таков:
Это уравнение пригодно всегда, за исключением двух случаев. При т = n уравнения вообще нет, а при т = n + 1 пара членов в (13.16) должна пропасть. Этими исключениями мы пренебрежем. Мы просто будем игнорировать тот факт, что некоторые из этих уравнений слегка меняются. Ведь как-никак кристалл считается бесконечным и слагаемых в гамильтониане бесчисленно много; пренебрежение некоторым их числом вряд ли сильно на чем-то скажется. Итак, в первом грубом приближении давайте позабудем об изменениях уравнений. Иными словами, допустим, что (13.16) верно при всех т и n, даже когда т и n стоят по соседству. Это самое существенное в нашем приближении.
Поразмыслим минутку о том, что было бы, если бы у нас были две независимые, отдельные спиновые волны (как в предыдущем параграфе), соответствующие k = k1 и k = k2; их энергии из (13.12) имели бы вид
Заметьте, что энергия Е в (13.19) является как раз их суммой:
Иными словами, наше решение можно толковать следующим образом. Имеются две частицы, т. е. пара спиновых волн, одна из которых обладает импульсом, описываемым числом k1 а другая — числом k2; энергия системы равна сумме энергий этих двух объектов. Обе частицы действуют совершенно независимо. Вот и все, что в этом есть — и ничего больше.
и с волновыми числами kс и к, связанными с k1 и k2 формулами
В этом решении отражено и «взаимодействие» пары спинов. Оно описывает тот факт, что когда спины сближаются, возникает какая-то вероятность их рассеяния. Поведение спинов очень похоже на взаимодействие частиц. Но подробная теория их рассеяния выходит за пределы того, о чем мы здесь собрались говорить.) СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

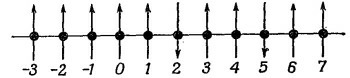 Теперь мы хотели бы выяснить, что происходит, когда имеется пара перевернутых спинов. Опять начнем с выбора системы базисных состояний. Выберем такие состояния, когда спины перевернуты в каких-то двух местах (так, как на фиг. 13.2). Эти состояния можно, скажем, отмечать х-координатами тех двух узлов решетки, в которых оказались электроны с перевернутым спином. То, что на рисунке, можно обозначить |х2, х5>. В общем случае базисные состояния будут |хn, хт> — дважды бесконечная совокупность! При таком способе описания состояние | x4, х9> и состояние | х9, x4> совпадают, потому что каждое из них просто говорит, что в точках 4 и 9 спин перевернут; порядок их не имеет значения. Не имзет также смысла состояние | x4, x4 > — такого просто быть не может. Любое состояние |ψ> мы можем описать, задав амплитуды того, что оно обнаружится в одном из базисных состояний.
Теперь мы хотели бы выяснить, что происходит, когда имеется пара перевернутых спинов. Опять начнем с выбора системы базисных состояний. Выберем такие состояния, когда спины перевернуты в каких-то двух местах (так, как на фиг. 13.2). Эти состояния можно, скажем, отмечать х-координатами тех двух узлов решетки, в которых оказались электроны с перевернутым спином. То, что на рисунке, можно обозначить |х2, х5>. В общем случае базисные состояния будут |хn, хт> — дважды бесконечная совокупность! При таком способе описания состояние | x4, х9> и состояние | х9, x4> совпадают, потому что каждое из них просто говорит, что в точках 4 и 9 спин перевернут; порядок их не имеет значения. Не имзет также смысла состояние | x4, x4 > — такого просто быть не может. Любое состояние |ψ> мы можем описать, задав амплитуды того, что оно обнаружится в одном из базисных состояний.