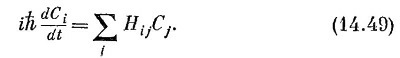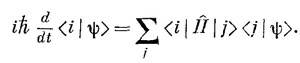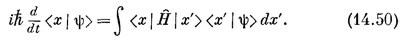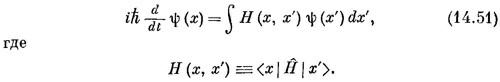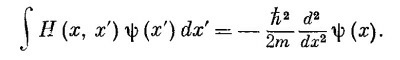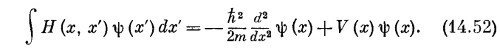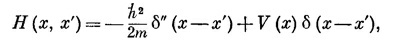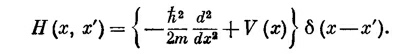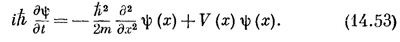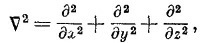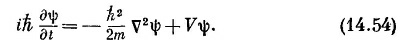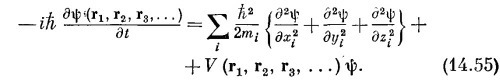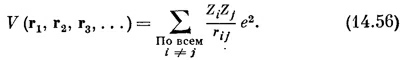Главная >> Фейнмановские лекции по физике >> Том 9 >> Глава 14. Зависимость амплитуд от места

Уравнение Шредингера

До сих пор мы просто заботились о том, как бы записать состояния, которые бы учитывали, что электрон может находиться в пространстве где угодно. Теперь же следует позаботиться о включении в наше описание физики того, что может произойти в тех или иных обстоятельствах. Как и прежде, надо подумать о том, как состояния будут меняться со временем. Если у нас есть состояние | ψ>, которое несколько позже переходит в другое состояние | ψ′>, то положение в любой момент мы сможем описать, сделав волновую функцию (т. е. попросту амплитуду <r | ψ>) функцией не только координат, но и времени. Частицу в данных условиях можно будет тогда описывать, задавая меняющуюся во времени волновую функцию ψ (r, t) =ψ (х, у, z, t). Эта меняющаяся во времени волновая функция описывает эволюцию последовательных состояний, которая происходит с течением времени. Это так называемое «координатное представление»; оно дает проекции состояния | ψ> на базисные состояния | r> и не всегда может считаться самым удобным, но мы с него и начнем.
 
В гл. 6 мы описали на языке гамильтониана Н_¡j, как состояния меняются во времени. Мы видели, что временная вариация различных амплитуд дается матричным уравнением

Это уравнение говорит, что изменение во времени каждой из амплитуд С_i пропорционально сумме всех прочих амплитуд С_j с коэффициентами H_ij.
 
Как должно выглядеть (14.49) при континууме базисных состояний |x>? Вспомним сперва, что (14.49) можно также записать в виде

Теперь ясно, что делать. Для x-представления следует писать

Сумма по базисным состояниям |j> заменяется интегралом по х′. Поскольку <x | Н | х′ > должна быть какой-то функцией от х и х′, запишем ее как Н (х, х′), что соответствует Н_¡j в (14.49). Тогда (14.50) это то же самое, что

Согласно (14.51), быстрота изменения ψ в точке х зависела бы от значений ψ во всех других точках х′; множитель Н (х, х′)— это амплитуда (в единицу времени) того, что электрон перепрыгнет из х′ в x.Оказывается, однако, что в природе эта амплитуда всюду, кроме точек х′, очень близких к х, равна нулю. Это означает, как мы видели на примере цепочки атомов в начале главы [см. (14.12)], что правая часть (14.51) может быть полностью выражена только через ψ и ее производные по х в точке х.
 
Для частицы, которая свободно движется в пространстве, не подвергаясь действию каких-либо сил и возмущений, правильный физический закон таков:

Откуда это получается? Это невозможно вывести из чего-либо нам уже известного. Это рождено в голове Шредингера, это выдумано им в битве за понимание эспериментальных наблюдений реального мира. Может быть, какой-то ключ к тому, почему так должно быть, вам дадут размышления по поводу нашего вывода уравнения (14.12), которое проистекло из рассмотрения распространения электрона в кристалле.  
Конечно, от свободных частиц проку мало. Что будет, если к частице приложить силы? Что ж, если действующая на частицу сила может быть описана с помощью скалярного потенциала V (х) (что означает, что речь идет не о магнитных силах, а об электрических) и если мы ограничимся низкими энергиями, чтобы иметь право пренебрегать теми сложностями, которые возникают при релятивистском движении, то гамильтониан, который укладывается в реальный мир, таков:

Опять-таки некоторый ключ к происхождению этого уравнения вы получите, если вернетесь к движению электрона в кристалле и посмотрите, как надо изменить уравнения, если энергия электрона медленно меняется от атома к атому, как если бы к кристаллу было приложено электрическое поле. Тогда член Е₀ в (14.7) будет медленно меняться в зависимости от места и будет соответствовать новому слагаемому, появившемуся в (14.52). [Вас может удивить, отчего мы сразу перешли от (14.51) к (14.52), а не дали правильного выражения для амплитуды Н (х, х′)= <х|Н|х′>. Да потому, что Н (х, х′) можно написать только с помощью необычных алгебраических функций, а интеграл в правой части (14.51) выражается через привычные вещи. Если вам это в самом деле интересно, то вот смотрите: Н (х, х`) можно записать так:

где δ″ означает вторую производную δ-функции. Эту довольно странную функцию можно заменить чуть более удобным и полностью ей равнозначным алгебраическим выражением

Мы не будем пользоваться этими формулами, а прямо будем работать с (14.52).]
 
Если теперь взять выражение (14.52) и подставить в (14.50) вместо интеграла, то для ψ(х) = <х |ψ> получится дифференциальное уравнение

Совершенно очевидно, что надлежит поставить вместо (14.53), если нас интересует трехмерное движение. Надо только d²/dx² заменить на

а V (х) заменить на V(x, у, z). Для электрона, движущегося в поле с потенциалом V (х, у, z), амплитуда ψ(х, у, z) удовлетворяет дифференциальному уравнению

Называется оно уравнением Шредингера и было первым известным квантовомеханическим уравнением. Его написал Шредингер, прежде чем было открыто любое другое описанное в этом томе уравнение.
 
Хотя мы здесь пришли к нему совсем иным путем, но появление этого уравнения в 1926 г., когда Шредингер впервые его написал, явилось великим историческим моментом, отметившим рождение квантовомеханического описания материи. Многие годы внутренняя атомная структура вещества была великой тайной. Никто не был в состоянии понять, что скрепляет вещество, отчего существут химическая связь, и, особенно, как атомам удается быть устойчивыми. Хотя Бор и смог дать описание внутреннего движения электрона в атоме водорода, которое, казалось бы, объясняло наблюдаемый спектр лучей, испускаемых этим атомом, но причина, отчего электроны движутся именно так, оставалась тайной. Шредингер, открыв истинные уравнения движения электронов в масштабах атома, снабдил нас теорией, которая позволила рассчитать атомные явления количественно, точно и подробно. В принципе его уравнение способно объяснить все атомные явления, кроме тех, которые связаны с магнетизмом и теорией относительности. Оно объясняет уровни энергии атома и все, что касается химической связи. Но, конечно, это объяснение только в принципе. Математика вскоре становится столь сложной, что точно решить удается только, простейшие задачи. Одни лишь атомы водорода и гелия были рассчитаны с высокой точностью. Однако путем различных приближений, порой весьма сомнительных, можно многое понять и в более сложных атомах и в химической связи молекул. Некоторые из этих приближений были показаны в предыдущих главах.
 
Уравнение Шредингера в том виде, в каком мы его записали, не учитывает каких-либо магнитных эффектов. Их, правда, можно приближенно принять во внимание, добавив в уравнение еще другие члены. Но, как мы убедились раньше, магнетизм — это эффект существенно релятивистский, так что правильное описание движения электрона в произвольном электромагнитном поле можно обсуждать только в рамках надлежащего релятивистского уравнения. Правильное релятивистское уравнение для движения электрона было открыто Дираком через год после того, как Шредингер придумал свое уравнение; оно имеет совершенно другой вид. Мы его не успеем здесь изучить.
 
Прежде чем перейти к рассмотрению некоторых следствий из уравнения Шредингера, хотелось бы продемонстрировать, как оно выглядит для системы многих частиц. Мы не будем им пользоваться, а просто хотим показать вам его, чтобы подчеркнуть, что волновая функция ψ не просто обычная волна в пространстве, а функция многих переменных. Если частиц много, уравнение превращается в

Потенциальная функция V — это то, что классически соответствует полной потенциальной энергии всех частиц. Если на частицы не действуют внешние силы, то функция V есть попросту электростатическая энергия взаимодействия всех частиц. Иначе говоря, если заряд ¡-й частицы равен Z_¡q_e, то функция V просто равна

СМОТРИТЕ ТАКЖЕ: