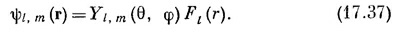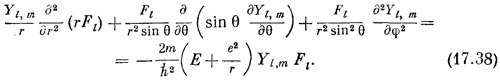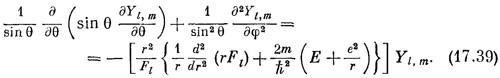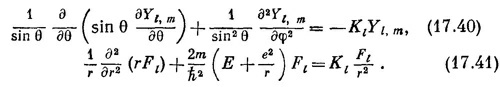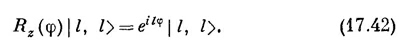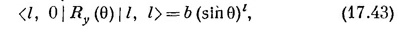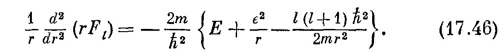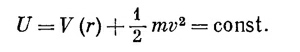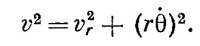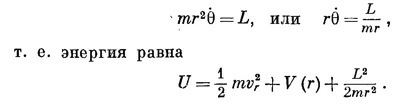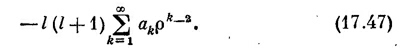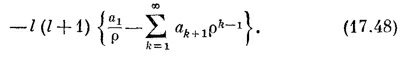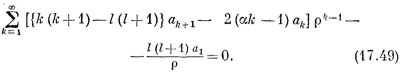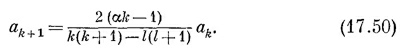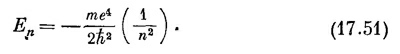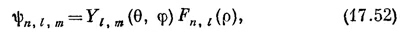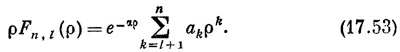| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Общее решение для водорода
В уравнении (17.35) мы записали волновые функции атома водорода в виде
Эти волновые функции должны быть решениями дифференциального уравнения (17.7). Посмотрим, что это означает. Подставим (17.37) в (17.7); получим
Помножим все на r2/Fl и переставим члены; результат будет таков:
Левая часть этого уравнения зависит от θ и φ, а от r не зависит. Какое бы значение r мы ни взяли, от этого левая часть не изменится. Значит, тоже должно быть выполнено и для правой части. Хотя в выражении в квадратных скобках там и сям попадаются разные r, все выражение от r зависеть не может, иначе бы не получилось уравнение, которое годится для всех r. Кроме того, как вы видите, эта скобка не зависит ни от θ, ни от φ. Она должна быть постоянным числом. Его величина имеет право зато зависеть от значения / того состояния, которое мы изучаем, поскольку этому состоянию принадлежит функция Fl, поэтому постоянное число мы обозначим Кl. Уравнение (17.35), стало быть, равнозначно двум уравнениям
Теперь взглянем на то, что мы сделали. Для каждого состояния, описываемого числами I и m, мы знаем функции Yl,m; тогда из уравнения (17.40) можно определить Kl. Затем, подставив Кl в (17.41), мы получим дифференциальное уравнение для функции Fl (r). Если мы его сможем решить, то все множители, входящие в (17.37), нам станут известны, и мы узнаем ψ (r).
Матричный элемент Ry (θ) тоже совсем прост;
где b — некоторое число. Объединяя их, получаем
Подстановка этой функции в (17.40) даст
Теперь, когда мы определили Kl, уравнение (17.41) даст нам радиальную функцию Fl (r). Перед нами обычное уравнение Шредингера, у которого угловая часть заменена ее эквивалентом KlFl /r2. Перепишем (17.41) в той форме, в какой мы писали уравнение (17.8):
У потенциальной энергии появилась какая-то таинственная добавка. Хотя она появилась на свет после длинной серии математических шагов, тем не менее у нее простое физическое происхождение. Мы беремся рассказать о ее происхождении при помощи полуклассических аргументов. После этого она уже не покажется вам такой таинственной.
В общем случае v разлагается на радиальную компоненту vr и на касательную компоненту rθ, т. е.
Момент количества движения mr2θ тоже сохраняется; пусть он равняется L. Тогда можно написать
Если бы момента количества движения не было, у нас осталось бы только два первых члена. Добавление момента количества движения L изменяет энергию как раз так, как если бы к потенциальной энергии добавился член L2/2mr2. Но он почти точно совпадает с добавкой (17.46). Единственная разница в том, что вместо ожидаемого числителя l2h2(этого можно было бы ожидать) появляется комбинация I (l+1) h2. Но мы еще раньше видели [например, в гл. 34, § 7 (вып. 7)], что это обычная замена, к которой всегда приходится прибегать, если хотят, чтобы квази-классические рассуждения совпали с правильным квантовомеханическим расчетом. Поэтому новый член можно понимать как своего рода «потенциал», определяющий «центробежную силу» и возникающий в уравнениях радиального движения вращающейся системы [см. гл. 12, § 5 (вып. 1)].
Его можно записать еще и так:
(Мы выделили первый член, а затем текущий индекс k сдвинули на единицу.) Вместо (17.20) появится
Поскольку член с ρ–1 только один, то он должен обратиться в нуль. Коэффициент а1 должен быть равен нулю (если только I не равно нулю, но тогда мы приходим к нашему прежнему решению). А когда все квадратные скобки при любых k обратятся в нуль, то и все следующие члены станут равны нулю. Из-за этого условие (17.21) переходит в
Это единственное существенное видоизменение по сравнению со сферически симметричным случаем.
Волновая функция состояния с такой энергией и с угловыми квантовыми числами / и m имеет вид
где
Коэффициенты ak получаются из (17.50). Наконец-то в наших руках полное описание состояний атома водорода. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.