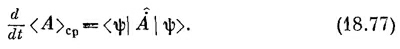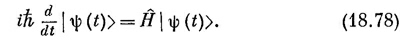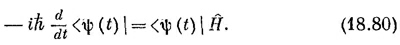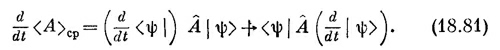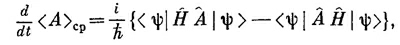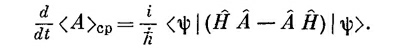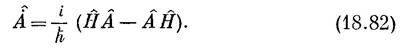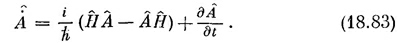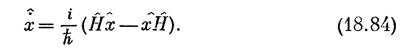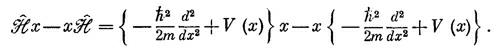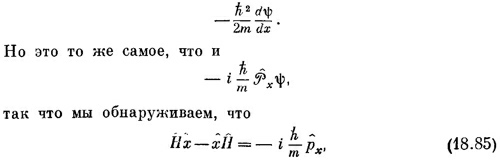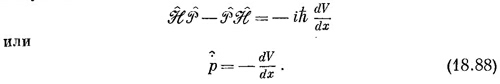Главная >> Фейнмановские лекции по физике >> Том 9 >> Глава 18. Операторы

Изменение средних со временем

Теперь мы познакомим вас с еще одной интересной вещью: вы узнаете, как средние изменяются во времени. Представим на минуту, что у нас есть оператор A, в который время явным образом не входит. Имеется в виду такой оператор, как х или р. [А исключаются, скажем, такие вещи, как оператор внешнего потенциала V(x, t), меняющийся во времени.] Теперь представим, что мы вычислили <A>_ср в некотором состоянии |ψ>, т. е.

Как <A>_ср будет зависеть от времени? Но почему оно вообще может зависеть от времени? Ну, во-первых, может случиться, что оператор сам явно зависит от времени, например, если он был связан с переменным потенциалом типа V(x, t). Но даже если оператор от t не зависит, например оператор А=х, то соответствующее среднее может зависеть от времени. Ведь среднее положение частицы может перемещаться. Но как может такое движение получиться из (18.76), если А от времени не зависит? Дело в том, что во времени может меняться само состояние |ψ>. Для нестационарных состояний мы часто даже явно отмечали зависимость от времени, записывая их как |ψ(t)>. Теперь мы хотим  показать, что   скорость изменения <A>_ср дается новым оператором, который мы обозначим А. Напомним, что A это оператор, так что точка над А вовсе не означает дифференцирования по времени, а является просто способом записи нового оператора А, определяемого равенством

Задачей нашей будет найти оператор A.
 
Прежде  всего, нам  известно, что скорость изменения состояния дается гамильтонианом.  В частности,

Это всего-навсего абстрактная форма записи  нашего первоначального определения гамильтониана

Если мы комплексно сопряжем это уравнение, оно будет эквивалентно

Посмотрим теперь, что случится, если мы продифференцируем (18.76)  по t. Поскольку каждое  ψ  зависит от t, мы имеем

Наконец,  заменяя производные их выражениями  (18.78) и (18.80), получаем

а это то же самое, что написать

Сравнивая это уравнение с (18.77), мы видим, что

Это и есть то интересное соотношение, которое мы обещали; и оно справедливо для любого оператора А.
 
Кстати заметим, что, если бы оператор А сам зависел от времени, мы бы получили

Проверим (18.82) на каком-либо примере, чтобы посмотреть, имеет ли оно вообще смысл. Какой, например, оператор соответствует х? Мы утверждаем, что это должно быть

Что это такое? Один способ установить, что это такое — перейти в координатное представление и воспользоваться алгебраическим оператором H. В этом представлении коммутатор равен

Если вы подействуете всем этим выражением на волновую функцию ψ(x) и вычислите везде, где нужно, производные, вы в конце концов получите

или что

Прелестный результат. Он означает, что если среднее значение х меняется со временем, то перемещение центра тяжести равно среднему импульсу, деленному на массу т. Точно кай в классической механике.
 
Другой пример. Какова скорость изменения среднего импульса состояния? Правила игры прежние. Оператор этой скорости равен

Опять все можно подсчитать в x-представлении. Напомним, что р обращается в d/dx, а это означает, что вам придется дифференцировать потенциальную энергию V (в H), но только во втором слагаемом. В конце концов остается только один член, и вы получаете

Опять классический результат. Справа стоит сила, так что мы вывели закон Ньютона! Но помните — это законы для операторов, которые дают средние величины. Они не описывают в деталях, что происходит внутри атома.
 
Существенное отличие квантовой механики в том, что рх не равно хр. Они отличаются на самую малость — на маленькое число h. Но все поразительные сложности интерференции волн и тому подобного проистекают из того небольшого факта, что хр—рх не совсем нуль.
 
История этой идеи тоже интересна. С разницей в несколько месяцев в 1926 г. Гейзенберг и Шредингер независимо отыскали правильные законы, описывающие атомную механику. Шредингер изобрел свою волновую функцию ψ (x) и нашел уравнение для нее, а Гейзенберг обнаружил, что природу можно было бы описывать и классическими уравнениями, лишь бы хр—рх было равно h/i, чего можно было добиться, определив их с помощью особого вида матриц. На пашем теперешнем языке он пользовался энергетическим представлением и его матрицами. И то и другое — и матричная алгебра Гейзенберга и дифференциальное уравнение Шредингера — объясняли атом водорода. Несколькими месяцами позднее Шредингер смог показать, что обе теории эквивалентны — мы только что это видели. Но две разные математические формы квантовой механики были открыты независимо.

СМОТРИТЕ ТАКЖЕ: