Главная >> Фейнмановские лекции по физике >> Том 10 >> Задачи к томам V-VII 6. Электродинамика
 К главе 15. Векторный потенциал К главе 15. Векторный потенциал
15.1. Внутри сверхпроводника поля В и Е равны нулю.
а) Граничным условием для поля Е на поверхности сверхпроводника является равенство нулю его тангенциальных компонент. Как выглядят граничные условия для магнитного поля?
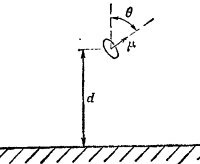
б) Маленькая рамка с током помещена на расстоянии d от поверхности сверхпроводника, занимающего полупространство. Магнитный момент μ рамки образует угол θ с нормалью к поверхности. Несколькими словами опишите метод, с помощью которого можно найти магнитное поле в любой точке пространства, предполагая, что поле магнитного диполя уже известно.
в) Найдите зависимость от угла θ вращающего момента, приложенного к диполю. Найдите углы, соответствующие равновесию диполя. Какие из них отвечают устойчивому равновесию, а какие — неустойчивому?
г) Найдите зависимость от угла θ силы, притягивающей магнитный диполь к сверхпроводнику или отталкивающей диполь от него.
 К главе 17. Законы индукции К главе 17. Законы индукции
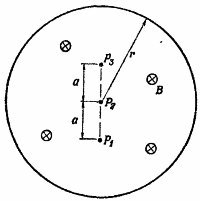
17.1. На приведенном рисунке изображено однородное магнитное поле В внутри цилиндра радиуса r. Напряженность магнитного поля В уменьшается с постоянной скоростью 100 гс/сек. Чему равно мгновенное ускорение (величина и направление) электрона, помещенного в точки Р1 Р2 и Р3? Величину а считать равной 5,0 см.
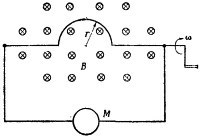 17.2. Жесткий провод, согнутый в полукруг радиуса r, вращается с угловой скоростью ω в однородном магнитном поле. Чему равна частота и амплитуда напряжения и тока, наведенного в проводнике, если внутреннее сопротивление вольтметра М равно RM, а сопротивление остальных частей цепи ничтожно? Предположите, что поле, создаваемое током, мало по сравнению с полем В, т. е. наведенный ток мал и неспособен существенно изменить величину В. 17.2. Жесткий провод, согнутый в полукруг радиуса r, вращается с угловой скоростью ω в однородном магнитном поле. Чему равна частота и амплитуда напряжения и тока, наведенного в проводнике, если внутреннее сопротивление вольтметра М равно RM, а сопротивление остальных частей цепи ничтожно? Предположите, что поле, создаваемое током, мало по сравнению с полем В, т. е. наведенный ток мал и неспособен существенно изменить величину В.
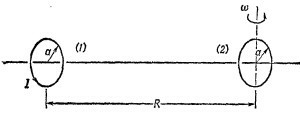 17.3. По круговому витку (1) провода, радиус а которого мал, течет постоянный ток /. Другой точно такой же виток провода (2) помещен на оси, проходящей через центр первого витка, на расстоянии R, причем R»a. Плоскости витков параллельны. Затем виток (2) приводится во вращение с угловой скоростью ω вокруг одного из его диаметров. Какова наведенная в цепи витка (2) э. д. с, если он разомкнут? 17.3. По круговому витку (1) провода, радиус а которого мал, течет постоянный ток /. Другой точно такой же виток провода (2) помещен на оси, проходящей через центр первого витка, на расстоянии R, причем R»a. Плоскости витков параллельны. Затем виток (2) приводится во вращение с угловой скоростью ω вокруг одного из его диаметров. Какова наведенная в цепи витка (2) э. д. с, если он разомкнут?
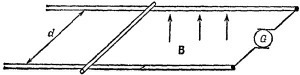 17. 4. Металлический провод массы т скользит без трения по двум параллельным металлическим рельсам, находящимся на расстоянии d друг от друга, как показано на рисунке. При движении провод пересекает силовые линии однородного магнитного поля В, направленного вертикально. 17. 4. Металлический провод массы т скользит без трения по двум параллельным металлическим рельсам, находящимся на расстоянии d друг от друга, как показано на рисунке. При движении провод пересекает силовые линии однородного магнитного поля В, направленного вертикально.
а) Генератор G создает постоянный ток /, текущий от одного рельса к другому через скользящий провод; Определите скорость (величину и направление) провода как функцию времени, предполагая, что в момент t=0 провод покоился.
б) Генератор заменяется электрической батареей с постоянной э. д. с. Провод при этом движется с постоянной скоростью. Найдите скорость установившегося движения. Достигает ли скорость такой величины в условиях задачи (а)?
в) Чему равен ток в задаче (б) в условиях установившегося движения? Считайте, что магнитное поле, создаваемое током /, значительно меньше В.
17. 5. Цепь состоит из двух соединенных последовательно катушек с индуктивностями L1 и L2. Взаимная индукция катушек равна M. Найдите полную индуктивность цепи. Как изменится суммарная индуктивность, если витки одной катушки перемотать в другую сторону?
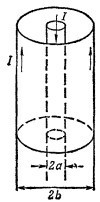 17.6. Кабель сделан из провода и охватывающего его коаксиального проводящего цилиндра, по которому течет ток в противоположном направлении. Радиус внутреннего провода кабеля равен а, а внешний радиус цилиндра равен b. 17.6. Кабель сделан из провода и охватывающего его коаксиального проводящего цилиндра, по которому течет ток в противоположном направлении. Радиус внутреннего провода кабеля равен а, а внешний радиус цилиндра равен b.
а) Покажите, что если предположить, что ток во внутреннем проводе течет только по его поверхности, то индуктивность, приходящаяся на единицу длины кабеля, равна
б) Вычислите индуктивность, если ток равномерно распределен по сечению внутреннего провода кабеля. Сравните оба полученных результата. Сильно ли зависит результат от характера распределения тока по сечению центрального провода?
17.7. Тороидальная катушка из N витков, внутренний радиус которой равен b, в поперечном сечении имеет форму квадрата со сторонами, равными а.
а) Покажите, что индуктивность катушки равна
б) Выразите через те же величины взаимную индукцию системы, состоящей из тороидальной катушки и длинного прямолинейного провода, вытянутого вдоль оси симметрии катушки. Считайте, что проводники, замыкающие цепь, настолько удалены от катушки, что их влиянием можно пренебречь.
в) Найдите отношение индуктивности катушки к взаимной индукции системы.
 17.8. Два плоских витка провода с одинаковой площадью А и током / помещены на расстоянии r друг от друга так, как показано на рисунке. Единичные векторы n1 и n2, определяющие направления нормалей к виткам, образуют с линией, соединяющей центры витков, углы α1 и α2 и лежат с ней в одной плоскости. 17.8. Два плоских витка провода с одинаковой площадью А и током / помещены на расстоянии r друг от друга так, как показано на рисунке. Единичные векторы n1 и n2, определяющие направления нормалей к виткам, образуют с линией, соединяющей центры витков, углы α1 и α2 и лежат с ней в одной плоскости.
а) Предполагая, что радиус каждого витка во много раз меньше r, найдите взаимную индукцию M двух витков.
б) Используя найденное выражение для M12, найдите величину и направление силы, действующей между витками.
в) Как изменится эта сила, если направление тока в одном из витков или сразу в обоих поменять на противоположное?
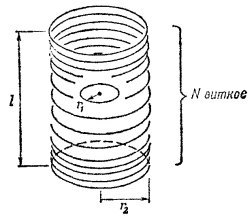 17.9. Круговой виток провода радиуса r1 расположен в центре соленоида длиной /, состоящего из N витков радиуса r2, причем r2»r1. Оси витка и соленоида совпадают. Обозначив цепь кругового витка индексом 1, а цепь соленоида индексом 2, найдите индуктивности M12 и M21. 17.9. Круговой виток провода радиуса r1 расположен в центре соленоида длиной /, состоящего из N витков радиуса r2, причем r2»r1. Оси витка и соленоида совпадают. Обозначив цепь кругового витка индексом 1, а цепь соленоида индексом 2, найдите индуктивности M12 и M21.
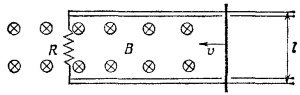 17.10. В однородном магнитном поле В, направленном перпендикулярно плоскости рисунка, по двум проводящим рельсам со скоростью v движется провод. Какой ток течет через сопротивление R, если v = 100 см/сек, /=10 см, В =0,1 вебер/м2 и R=10 ом (магнитным полем, создаваемым током, пренебречь). В какую сторону изменится найденный вами ток, если не пренебрегать полем, создаваемым движущимся проводником? Изменится ли ваш ответ, если магнит, создающий поле В, будет двигаться со скоростью v в ту же сторону, что и провод? Как меняется со временем коэффициент самоиндукции изображенной на рисунке цепи? 17.10. В однородном магнитном поле В, направленном перпендикулярно плоскости рисунка, по двум проводящим рельсам со скоростью v движется провод. Какой ток течет через сопротивление R, если v = 100 см/сек, /=10 см, В =0,1 вебер/м2 и R=10 ом (магнитным полем, создаваемым током, пренебречь). В какую сторону изменится найденный вами ток, если не пренебрегать полем, создаваемым движущимся проводником? Изменится ли ваш ответ, если магнит, создающий поле В, будет двигаться со скоростью v в ту же сторону, что и провод? Как меняется со временем коэффициент самоиндукции изображенной на рисунке цепи?
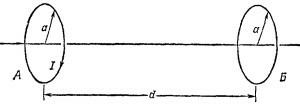 17.11. Рассмотрим два витка провода радиуса а, находящиеся на расстоянии d друг от друга (d»a). Центры витков лежат на одной прямой, перпендикулярной плоскости обоих витков. Через виток А в направлении, показанном на рисунке стрелкой, пропускается ток /=K0t2 (t — время). Сопротивление витка Б равно R. 17.11. Рассмотрим два витка провода радиуса а, находящиеся на расстоянии d друг от друга (d»a). Центры витков лежат на одной прямой, перпендикулярной плоскости обоих витков. Через виток А в направлении, показанном на рисунке стрелкой, пропускается ток /=K0t2 (t — время). Сопротивление витка Б равно R.
а) Если пренебречь самоиндукцией витков, то чему равен момент сил, действующих на виток Б?
б) Покажите, что если пренебречь самоиндукцией, то сила, действующая на виток Б, равна
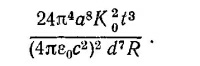 |
В какую сторону направлена эта сила?
в) Покажите качественно, в каком направлении изменится найденная вами величина силы и величина момента силы, если самоиндукцией витков не пренебрегать?
г) Выясните, как изменится ответ к пунктам (а) и (б) задачи, если виток Б повернуть на 90° вокруг оси, перпендикулярной общей оси витков.
К главе 20. Решения уравнений Максвелла в пустом пространстве
20.1. Решение дифференциальных уравнений иногда удобно искать в комплексном виде,
а) Покажите, что если электрическое поле зависит от времени t и координаты х (зависимости от у и z нет)
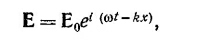 |
то каждая компонента вектора напряженности электрического поля удовлетворяет волновому уравнению. (Напомним, что физическое поле описывается вещественной частью приведенного выражения.)
б) Убедитесь, что вещественная часть Е описывает плоскую волну, распространяющуюся вдоль оси х. В какую сторону оси х распространяется волна?
в) Покажите, что если оператор V действует на функции, подобные приведенной в пункте (а), то он имеет вид
где ex— единичный вектор, направленный вдоль оси х; i=√–1 — мнимая единица, т. е. что его действие сводится к простому умножению функции на число. Можно ли подобное утверждать относительно оператора производной по времени?
г) Используя результат пункта (в), покажите, какой вид имеют уравнения Максвелла для полей, зависящих от t и х синусоидально. Какая связь должна существовать между ω и k?
д) Как изменятся ваши ответы, если электрическое поле имеет вид
20.2. Плоская электромагнитная волна частоты ω отражается от зеркала, движущегося со скоростью v в направлении распространения волны. Используя уравнения Максвелла, найдите частоту отраженной волны, которая регистрируется неподвижным наблюдателем. Сравните ваш результат с тем, который был получен в вып. 3 с помощью теории относительности.
К главе 21. Решения уравнений Максвелла с токами и зарядами
21.1. Выведите подробно выражение (21.26) (см. «Лекции», вып. 6, стр. 155).
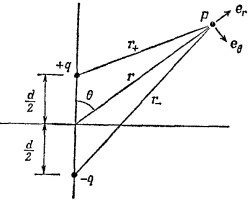 21.2. С помощью уравнения (21.1) (см. вып. 6, стр. 142) можно найти электрическое поле, создаваемое движущимся зарядом. Рассмотрим диполь, образованный положительным и отрицательным зарядами, осциллирующими относительно начала координат вдоль оси z так, что координата положительного заряда меняется со временем по закону z+=d/2cosω t, а отрицательного z_=–d/2cosω t, Дипольный момент такой системы зарядов равен p=dez dcosω t. Покажите, что электрическое поле диполя, найденное из упомянутого уравнения, имеет вид 21.2. С помощью уравнения (21.1) (см. вып. 6, стр. 142) можно найти электрическое поле, создаваемое движущимся зарядом. Рассмотрим диполь, образованный положительным и отрицательным зарядами, осциллирующими относительно начала координат вдоль оси z так, что координата положительного заряда меняется со временем по закону z+=d/2cosω t, а отрицательного z_=–d/2cosω t, Дипольный момент такой системы зарядов равен p=dez dcosω t. Покажите, что электрическое поле диполя, найденное из упомянутого уравнения, имеет вид
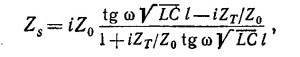 |
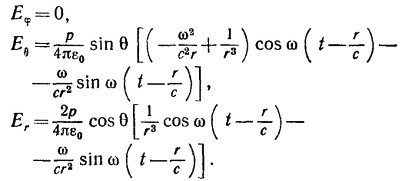 |
При решении задачи считайте, что точка Р находится на расстоянии r»d от диполя.
Примечание. еr+≈еr≈еr_, a der+ /dt и d2er+/dt2 — это векторы, направления которых практически совпадают с направлением вектора еθ.
21.3. Используя симметрию уравнений Максвелла и вид электрического и магнитного полей осциллирующего электрического диполя, найдите поле осциллирующего магнитного диполя. Это поле должно совпадать с полем диполя, создаваемого контуром с током i=i0cosω t, радиус которого равен a (a«c/ω).
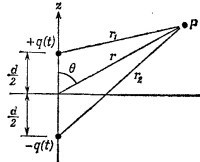 21.4. В задаче 21.2 диполь состоял из двух зарядов, осциллирующих вокруг начала координат. Диполь, величина которого изменяется со временем по гармоническому закону, можно построить иным способом: взять два проводящих шара, соединить их проводником длиной d и по проводнику пропустить переменный ток. Тогда на концах проводника возникает переменный заряд ±q(t), a сам проводник остается в целом нейтральным; заряд q(t) можно рассматривать как вещественную часть выражения Q0e¡ωt. 21.4. В задаче 21.2 диполь состоял из двух зарядов, осциллирующих вокруг начала координат. Диполь, величина которого изменяется со временем по гармоническому закону, можно построить иным способом: взять два проводящих шара, соединить их проводником длиной d и по проводнику пропустить переменный ток. Тогда на концах проводника возникает переменный заряд ±q(t), a сам проводник остается в целом нейтральным; заряд q(t) можно рассматривать как вещественную часть выражения Q0e¡ωt.
В произвольной точке Р на расстоянии r»d от диполя интегральное представление для запаздывающего потенциала приводит к точному выражению для φ (см. рисунок)
б) Покажите далее, что
в) Убедитесь, что из найденных вами потенциалов следуют те же выражения для электрического и магнитного полей.
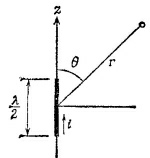 21.5. Антенна, предназначенная для работы на частоте ω=2πс/λ, изготовлена из двух колинеарных проводов, длина каждого из которых равна 1/4 длины волны. На антенну подается синусоидальное меняющееся напряжение требуемой частоты. Возникающее в антенне распределение токов с большой степенью точности описывается выражением 21.5. Антенна, предназначенная для работы на частоте ω=2πс/λ, изготовлена из двух колинеарных проводов, длина каждого из которых равна 1/4 длины волны. На антенну подается синусоидальное меняющееся напряжение требуемой частоты. Возникающее в антенне распределение токов с большой степенью точности описывается выражением
Для определения поля излучения антенну можно представить в виде суперпозиции большого числа диполей длины Δz, причем каждый из них расположен в точке z. Величина дипольного момента меняется от диполя к диполю.
а) Покажите, что дипольный момент каждого такого диполя следует брать в виде
б) Покажите, что на больших расстояниях (r»с/ω) электрическое и магнитное поля антенны имеют вид.
в) Нарисуйте примерный вид кривой зависимости Eθ, от угла θ. На этом же рисунке нанесите кривую зависимое ти Еθ. от θ для одного диполя и сравните полученные кривые.
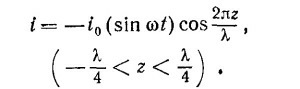 |
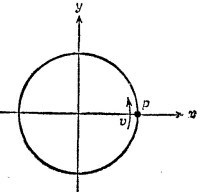 21.6. Частица с зарядом со скоростью v. 21.6. Частица с зарядом со скоростью v.
а) Найдите скалярный потенциал φ в центре круга в тот момент, когда частица находится в точке Р.
б) Определите векторный потенциал А в центре круга в тот же момент.
в) Определив потенциалы в окрестности центра круга,воспользуйтесь выражениями (18.16), (18.19) («Лекции», вып. 6, стр. 90) и найдите электрическое и магнитное поля в центре. Как ориентирован вектор напряженности электрического поля по отношению к радиусу-вектору, проведенному в точку Р?
г) Вычислите эти поля, воспользовавшись формулой (21.1) (вып. 6, стр. 142). В этой задаче скорость v не предполагается малой по сравнению со скоростью света с.
К главе 22. Цепи переменного тока
22.1. Проволочки соединены так, что они образуют ребра куба, причем сопротивление каждого ребра 1 ом. Найдите сопротивление между различными парами вершин куба.
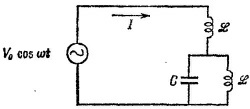 22.2. а) Найдите ток / в цепи, схема которой изображена на рисунке. 22.2. а) Найдите ток / в цепи, схема которой изображена на рисунке.
б) Чему равен ток /, если изображенные на схеме катушки индуктивности обладают взаимной индуктивностью M?
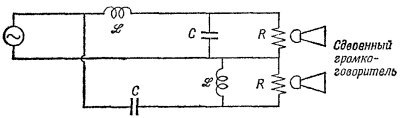 22.3. Принципиальная схема устройства высокой точности звуковоспроизведения имеет такой вид, как изображено на рисунке. Эффективное сопротивление каждого громкоговорителя равно R. 22.3. Принципиальная схема устройства высокой точности звуковоспроизведения имеет такой вид, как изображено на рисунке. Эффективное сопротивление каждого громкоговорителя равно R.
а) Покажите, что при R2=L/2C импеданс на входе (на клеммах генератора) веществен и равен R.
б) Покажите, что ω2=1/LC. Частота ωc определяется как та частота, при которой на каждый из громкоговорителей приходится 1/2 общей мощности.
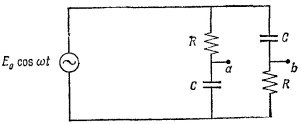 22.4. Покажите, что амплитуда разности потенциалов (напряжение) между точками а и b цепи, изображенной на схеме, не зависит от ω. Опишите качественно зависимость фазы этой разности потенциалов от частоты ω. Как изменится величина разности потенциалов между точками а и b, а также фаза, если источник напряжения обладает внутренним сопротивлением R10/? 22.4. Покажите, что амплитуда разности потенциалов (напряжение) между точками а и b цепи, изображенной на схеме, не зависит от ω. Опишите качественно зависимость фазы этой разности потенциалов от частоты ω. Как изменится величина разности потенциалов между точками а и b, а также фаза, если источник напряжения обладает внутренним сопротивлением R10/?
 22.5. Электрическая цепь имеет вид, изображенный на схеме. 22.5. Электрическая цепь имеет вид, изображенный на схеме.
а) Изобразите схематически зависимость амплитуды тока в цепи от частоты для произвольно выбранных величин L, С и R.
б) Если R» √L/C, сравните частоту резонанса и ширину пика резонансной кривой данной цепи с аналогичными величинами для цепи с последовательным соединением ее элементов, но при R«√LlC. Специально рассмотрите случай R=K√L/C для цепи с параллельным соединением и случай R=(1/K)√L/C для цепи с последовательным соединением
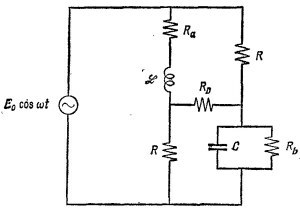 22.6. Мостовая схема, изображенная на рисунке, используется для измерений индуктивности. Источником переменной э. д. с. частоты ω служит генератор напряжения. Если мост сбалансирован, ток через детектор RD равен нулю. Найдите L как функцию R и С. 22.6. Мостовая схема, изображенная на рисунке, используется для измерений индуктивности. Источником переменной э. д. с. частоты ω служит генератор напряжения. Если мост сбалансирован, ток через детектор RD равен нулю. Найдите L как функцию R и С.
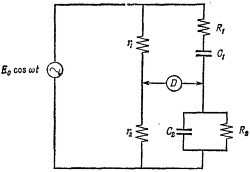 22.7. Изображенная схема представляет собой мост Вейна, часто используемый в RС-цепях. Если ток через детектор равен нулю, говорят, что мост сбалансирован. Покажите, что баланс наступает при одновременном выполнении следующих двух условий: 22.7. Изображенная схема представляет собой мост Вейна, часто используемый в RС-цепях. Если ток через детектор равен нулю, говорят, что мост сбалансирован. Покажите, что баланс наступает при одновременном выполнении следующих двух условий:
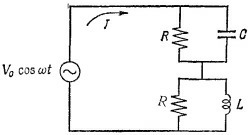 22.8. В цепи, изображенной на рисунке, действует источник переменного напряжения V(t)=V0cosωt. 22.8. В цепи, изображенной на рисунке, действует источник переменного напряжения V(t)=V0cosωt.
а) Покажите, что если R, L и С подобраны так, что RC=L/R, ток / в цепи не зависит от частоты.
б) Какова разность фаз между приложенным напряжением и напряжением на концах RC-пары (при RC=L/R)?
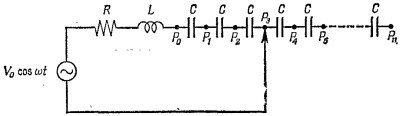 22.9. Электрическая цепь собрана так, что один ее свободный конец, изображенный на рисунке стрелкой, упирающейся в точку Р3, может быть присоединен к любой из точек Р0, Ри1 ..., Рn. 22.9. Электрическая цепь собрана так, что один ее свободный конец, изображенный на рисунке стрелкой, упирающейся в точку Р3, может быть присоединен к любой из точек Р0, Ри1 ..., Рn.
1. Найдите выражение для мощности, выделяемой в сопротивлении R, если цепь замкнута в точке Рm, где 0≤m≤n.
2. Допустим, что R=1000 ом, L=10 генри, С=20 мкф, ω=100 рад/сек.
а) При каком значении т найденная мощность максимальна?
б) Каково максимальное значение напряжения между точками Р0 и Р2 при m=2 и Vo= 100 в? На концах сопротивления R?
 К главе 23. Полые резонаторы К главе 23. Полые резонаторы
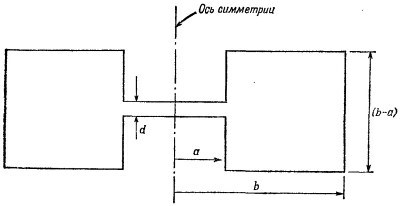
23.1. Найдите приближенно «резонансную» частоту для полости, изображенной на рисунке, предполагая, что d«a и d«(b—а). Какими основными эффектами вы пренебрегли? Если полость равномерно остывает (т. е. температура во всех точках полости в один и тот же момент времени одинакова), приведет ли ее тепловое сжатие к увеличению или уменьшению резонансной частоты? А может быть, она останется неизменной?
К главе 24. Волноводы
24.1. Единица длины линии передачи обладает индуктивностью Lo и емкостью Со. Покажите, что если напряжение V и ток / в линии передачи меняются медленно (что соответствует передаче сигналов с длиной волны, много большей, чем расстояние между секциями линии передачи), то V и / удовлетворяют следующим уравнениям:
Заметьте, что предположение о медленном изменении сигналов отнюдь не обязательно, но обоснование этого утверждения выходит за рамки гл. 24.
24. 2. Характеристический импеданс равен Z0=√L0/C0, где L0— индуктивность, а Со— емкость единицы длины.
Покажите, что для линии передачи, состоящей из двух тонких полос шириной b, находящихся на расстоянии а друг от друга (а«b), характеристический импеданс равен
24.3. Секция цилиндрической коаксиальной линии передачи закрыта с обоих концов проводящими пластинами. Длина полости, образованной таким способом, равна /. Для самой низкой моды, электрическое поле которой радиально:
а) найдите частоту;
б) найдите выражение для Е;
в) сравните найденную частоту с ωo=1/√L/C, где L— индуктивность, а С— емкость, приходящиеся на длину / бесконечной коаксиальной линии.
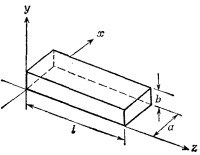 24.4. Волновод в форме прямоугольного параллелепипеда (стороны сечения а и b) изготовлен из идеального проводящего материала. Концы одной секции волновода, длина которой /, закрыты пластинами из проводящего материала, так что полость внутри волновода фактически представляет собой резонатор. Если электрическое поле в полости определяется вещественной частью выражения 24.4. Волновод в форме прямоугольного параллелепипеда (стороны сечения а и b) изготовлен из идеального проводящего материала. Концы одной секции волновода, длина которой /, закрыты пластинами из проводящего материала, так что полость внутри волновода фактически представляет собой резонатор. Если электрическое поле в полости определяется вещественной частью выражения
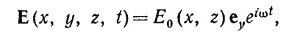 |
то чему равна амплитуда Е0(х, z) для колебания самой низкой резонансной частоты? Чему равна сама резонансная частота?
24.5. Коаксиальный кабель состоит из двух концентрических проводящих цилиндров. Один конец (х=0) кабеля подсоединен к генератору переменного напряжения V(t)=V0cosωt. Другой конец (х=l) закрыт проводящей пластиной. Индуктивность и емкость единицы длины кабеля равны L0 и С0. Поле в таком кабеле можно представить в виде суперпозиции двух волн: падающей и отраженной от закороченного конца. Амплитуды и фазы этих волн должна быть подобраны так, чтобы суммарное напряжение между проводниками было равно нулю при х=l и V0cosωt при х=0.
а) Напишите выражения для падающей и отраженной волн.
б) Нарисуйте кривую зависимости напряжения между проводниками от расстояния х, если длина кабеля / равна 5πс/2ω (с — скорость света). Укажите значения х, для которых напряжение максимально.
в) Чему равен ток в точках х=0, x=//2=1/2(5πс/2ω) и х=/=5πс/2ω?
г) Предполагая источник напряжения идеальным, определите средний момент сил, который должен быть приложен к его ротору, чтобы последний вращался с угловой скоростью ω.
 24.6. Покажите, что если при х=l линия передачи замкнута (включен элемент с импедансом ZT), to импеданс на «входе» линии (х=0) равен 24.6. Покажите, что если при х=l линия передачи замкнута (включен элемент с импедансом ZT), to импеданс на «входе» линии (х=0) равен
где Z0=√L/C— характеристический импеданс линии. Чему равно Zs, если
а) ZT=0?
б) ZT=∞?
в) ZT=Z0?
24.7. Линия передачи с характеристическим импедансом Z1 соединена с другой линией с характеристическим импедансом Z2.
Покажите, что если система работает от генератора, подключенного к первой линии (Z1), «коэффициент отражения», определяемый отношением Vотр/Vпад, равен
24.8. Электрические поля внутри волноводов, описанных в гл. 24 «Лекций», обладают тем свойством, что проекция вектора напряженности электрического поля на направление распространения волны равна нулю, т. е. электрическое поле поперечное. Кроме того, могут существовать бегущие волны, у которых равна нулю проекция напряженности магнитного поля на направление распространения (так называемые поперечные магнитные волны). Для волновода в форме прямоугольного параллелепипеда (см. «Лекции», вып. 6, стр. 224, фиг. 24.3 и 24.4) векторный потенциал поперечной магнитной волны имеет вид
а) Убедитесь, что магнитное поле, найденное с помощью этого потенциала, действительно поперечно, и покажите, что электрическое поле Е и магнитное поле В удовлетворяют волновому уравнению и соответствующим граничным условиям.
Примечание. Мы полагаем, что Е=–vφ– дА/dt, B=vxA, где v·А=–1/c2dφ/dt).
б) Покажите, что поперечная магнитная волна не распространяется, если
К главе 25. Электродинамика в релятивистских обозначениях
(Единицы измерения выбраны так, что с=1.)
25.1. Запишите в 4-векторной форме выражения
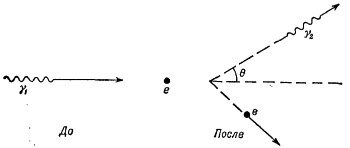 25.2. Комптон-эффект состоит в том, что фотон, налетая на покоящийся электрон, рассеивается на нем, как частица на частице. Выразите энергию рассеянного фотона через энергию падающего фотона и угол отклонения его направления распространения от первоначального. 25.2. Комптон-эффект состоит в том, что фотон, налетая на покоящийся электрон, рассеивается на нем, как частица на частице. Выразите энергию рассеянного фотона через энергию падающего фотона и угол отклонения его направления распространения от первоначального.
25.3. Позитрон может быть создан в результате бомбардировки покоящегося электрона фотоном:
Какова минимальная энергия фотона, необходимая для осуществления этого процесса? При решении задачи пользуйтесь, где это возможно, 4-векторами и их инвариантными комбинациями.
25. 4. На покоящуюся частицу массы т налетает другая частица с массой М и импульсом р. В результате полностью неупругого соударения частицы сливаются, образуя новую частицу. Какова масса и скорость этой частицы? Сравните ваш результат с тем, который получается в нерелятивистском приближении.
К главе 26. Лоренцевы преобразования полей
(Единицы измерения выбраны так, что с=1.)
26.1. Распишите подробно и вычислите выражение
26.2. Найдите 4-вектор, пространственные компоненты которого совпадают с компонентами вектора
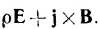 |
Каков физический смысл временной и пространственных компонент этого 4-вектора?
26.3. Покажите, что Е2—В2 и (Е·В) инвариантны относительно преобразований Лоренца. Убедитесь, что если векторы Е и В образуют острый угол в какой-нибудь системе координат, то этот угол будет острым во всех других системах координат. Для какого важного физического явления оба инварианта равны нулю?
26.4. Пусть Е и В — напряженности электрического и магнитного полей в некоторой точке пространства в данной системе координат. Определите скорость другой системы координат, в которой электрическое и магнитное поля параллельны. Систем координат, обладающих таким свойством, много. Действительно, если найдется хотя бы одна такая система координат, то указанные векторы будут параллельны и во всех других системах координат, движущихся с постоянной скоростью относительно найденной в направлении, общем для векторов Е′ и В′. Поэтому удобно и в тоже время достаточно рассмотреть систему координат, вектор скорости которой перпендикулярен к векторам Е и В.
26.5. В гл. 26 «Лекций» (вып. 6) 4-мерный потенциал Аμ, создаваемый движущейся с постоянной скоростью заряженной частицей, был найден путем перехода от системы координат, где частица покоится, к лабораторной системе координат. Напряженности Е и В электрического и магнитного полей с помощью Аμ определялись согласно общим формулам. Найдите Е и В, исходя из известного их вида в системе координат, где заряд покоится, и перейдя к движущейся системе координат.
26.6. Покажите, что электрическое и магнитное поля заряда, движущегося с постоянной скоростью, могут быть представлены в виде
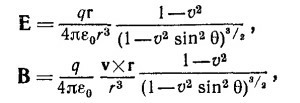 |
где r — радиус-вектор, проведенный из точки, где в данный момент находится заряд, в точку наблюдения, а θ — угол между векторами r и v.
26.7. По очень длинному прямому проводу течет ток /, создаваемый электронами, движущимися со скоростью v. Полная плотность зарядов в каждой точке провода равна нулю благодаря наличию положительно заряженных ионов.
а) Найдите поля вне провода в системе координат, где провод покоится.
б) Найдите те же поля в системе координат, движущейся вместе с электронами. В «Лекциях» электрическое поле в такой системе координат было найдено другим методом [см. вып. 5, стр. 271, выражение (13.28)].
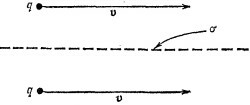 26.8. Два электрона с одинаковой скоростью v движутся параллельно друг другу по обе стороны от бесконечной положительно заряженной плоскости на расстоянии а от нее; плотность покоящихся поверхностных зарядов равна σ. 26.8. Два электрона с одинаковой скоростью v движутся параллельно друг другу по обе стороны от бесконечной положительно заряженной плоскости на расстоянии а от нее; плотность покоящихся поверхностных зарядов равна σ.
а) При какой величине σ расстояние между электронами будет оставаться равным 2 а?
б) Сравните величину σ, которая получается для электронов с энергией 500 Мэв, с той, которая будет в случае медленно движущихся электронов.
26.9. Пусть fμ— 4-вектор силы, действующей на частицу, а uμ—4-вектор ее скорости. Покажите, что
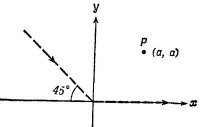 26.10. Частица с зарядом q движется с постоянной скоростью в плоскости ху вдоль траектории, изображенной на рисунке пунктирной линией (в начале координат частица рассеивается). Величина скорости частицы вдоль всей траектории остается постоянной. В момент времени t= t1 частица находится в точке х=а, у=0. 26.10. Частица с зарядом q движется с постоянной скоростью в плоскости ху вдоль траектории, изображенной на рисунке пунктирной линией (в начале координат частица рассеивается). Величина скорости частицы вдоль всей траектории остается постоянной. В момент времени t= t1 частица находится в точке х=а, у=0.
а) Найдите электрическое поле в точке Р (х=у=а) при t= t1 если v/с=0,5 (с — скорость света).
б) Как изменился бы ваш ответ, если бы до рассеяния в начале координат частица двигалась вдоль оси y?
К главе 27. Энергия поля и его импульс
27.1. Методом, использованным в «Лекциях» (вып. 6, стр. 288) при выводе выражения (27.11), представьте в ином виде выражения
 |
27.2. Выразите в мегатоннах (мгт) энергию магнитного поля Земли, заключенную во всем пространстве, внешнем по отношению к Земле (1 мгт — энергия, освобождаемая при взрыве 1 млн. тонн тринитротолуола, т. е. 4,2·1015 дж). Предположите, что магнитное поле Земли — это поле диполя с напряженностью на экваторе примерно около 2/3 гс (2/3·10–4 вебер/м2).
Как вы считаете, может ли водородная бомба 1 мгт,, взорванная высоко над поверхностью Земли, существенно исказить магнитное поле Земли?
27.3. Вычислите поток вектора Пойнтинга S через поверхность длинного прямолинейного провода, сопротивление единицы длины которого равно R. Сравните ваш результат с омическими потерями.
27.4. Длинный коаксиальный кабель изготовлен из двух идеально проводящих концентрических цилиндров. Один конец кабеля подсоединен к электрической батарее, напряжение на клеммах которой равно V. К другому концу кабеля присоединено сопротивление R. Следовательно, ток, протекающий по кабелю, равен I=V/R. С помощью вектора Пойнтинга вычислите скорость потока энергии.
27.5. Средняя мощность, излучаемая широковещательной станцией, составляет примерно 10 квт.
а) Чему равна величина вектора Пойнтинга на поверхности Земли в точках, удаленных от станции на 10 км? На таком расстоянии излучаемые волны можно считать плоскими. Разумно предположить, что вся мощность излучается 1/4λ, антенной, помещенной над идеально проводящей плоскостью.
б) Найдите максимальные значения напряженностей электрического и магнитного полей.
27.6. Поля, соответствующие наинизшей по частоте поперечной электрической волне в волноводе прямоугольного сечения (см. фиг. 24.6, вып. 6 «Лекций», стр. 227), имеют вид
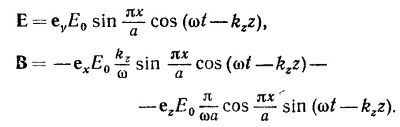 |
а) Покажите, что приведенное выше решение удовлетворяет граничным условиям задачи.
б) Вычислите вектор Пойнтинга S и плотность энергии U.
в) Вычислите средний поток энергии через поверхность, перпендикулярную оси z.
г) Вычислите среднюю плотность энергии в волноводе.
д) Используя результаты пунктов (в) и (г), вычислите среднюю скорость распространения энергии. Покажите, что эта скорость совпадает с групповой скоростью [см. формулу (24.27), вып. 6, стр. 229].
27.7. а) Найдите плотность потока энергии, излучаемой диполем с осциллирующим дипольным моментом р cosω t.
Примечание. Следует принять во внимание только члены, убывающие с расстоянием по закону 1/r.
б) Путем интегрирования по поверхности сферы большого радиуса, центр которой совпадает с диполем, покажите, что средняя излучаемая мощность равна
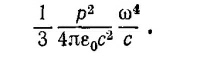 |
27.8. Плоская электромагнитная волна, падая на свободный электрон, заставляет его осциллировать. Найдите отношение энергии, излучаемой электроном в единицу времени, к плотности потока энергии падающей электромагнитной волны. Частота волны предполагается малой. Поэтому влиянием магнитного поля В волны на движение электрона можно пренебречь.
27.9. Частица пыли в Солнечной системе испытывает действие двух сил: силы притяжения к Солнцу и планетам и силы светового давления, пропорциональной ее поперечному сечению. Существует такой размер частицы, при котором эти силы уравновешивают друг друга. Предполагая, что частица имеет форму шарика и поглощает весь падающий на нее свет, найдите радиус частицы, отвечающий ее равновесию в поле этих двух сил. Объяснение того факта, что «хвосты» комет направлены в сторону от Солнца, покоится на предположении о существовании такого равновесия и о том, что «хвост» кометы состоит из частиц малого размера, возможно даже из молекул газа. Разумно ли такое объяснение? Мощность, излучаемая Солнцем, равна 4·1026 вт, его масса 2·1030 кг.
27.10. На полый тороид, средний радиус которого равен R, а радиус поперечного сечения r (r«R), намотано N витков проволоки. В момент времени t=0 по проволоке пропускается ток, сила которого нарастает со временем по линейному закону
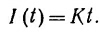 |
а) Найдите магнитное поле и энергию, запасенную в тороиде к моменту времени t.
б) Найдите направление и величину вектора Пойнтинга в любой внутренней точке тороида в момент времени t.
в) Используя вектор Пойнтинга, найдите скорость изменения со временем энергии электромагнитного поля внутри тороида в произвольный момент времени. Убедитесь в правильности вашего ответа, используя решение к пункту (а) задачи.
К главе 28. Электромагнитная масса
28.1. Предполагая, что энергия покоя электрона совпадает с его электростатической энергией и что заряд электрона равномерно распределен по объему сферы, вычислите радиус этой сферы. Сравните полученный результат с выражением Uэл=е2/2а [вып. 6, стр. 303, формула (28.2)].
28.2. Хорошо известно, что электроны, кроме заряда и массы, обладают еще и собственным моментом количества движения (спином) и магнитным моментом, которые связаны соотношением
 |
Это соотношение выполняется с точностью до 0,1%. Будем предполагать, что вся масса электрона электромагнитная, т. е. Мэ.м.=2е2/3ас2 [см. вып. 6, стр. 305, формула (28.4)].
а) В центре однородно заряженной сферической оболочки радиуса а и с полным зарядом q поместите магнитный диполь с магнитным моментом μ и покажите, что момент количества движения электромагнитного поля равен
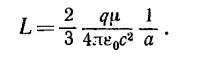 |
б) Определите отношение момента количества движения к магнитному моменту и сравните это отношение с величиной m/q.
в) Считая, что μz электрона равно hq/2m, вычислите максимальную скорость электрона на поверхности, обусловливающую данное значение магнитного момента. Приведите необходимые, с вашей точки зрения, пояснения. Величина (4πε0ch/q2)=1/α равна 137.
К главе 29. Движение зарядов в электрическом и магнитном полях
29.1. Заряженная частица (заряд q, масса покоя m0) в момент времени t=0 покоится в начале координат. Затем на нее начинает действовать постоянное электрическое поле, направленное вдоль оси х.
а) Вычислите релятивистскую скорость и координаты частицы как функции времени.
б) Как изменится ваш ответ, если в начальный момент частица имела скорость v0, направленную вдоль оси у?
29.2. В циклотроне протоны движутся в однородном магнитном поле по круговым траекториям. Найдите зависимость «циклотронной частоты» и угловой скорости протонов от q, В, т для протонов низкой энергии. Как изменится значение циклотронной частоты при увеличении энергии? При каком изменении энергии частота изменится на 1%?
29.3. В момент времени t=0 частица массы т с зарядом q покоится в начале координат. На частицу действует однородное электрическое поле Е, направленное по оси у, и однородное магнитное поле В, направленное по оси z.
а) Найдите последующее движение частицы, т. е. ее координаты x(t), y(t), z(t), предполагая движение нерелятивистским. Какое условие на Е и В накладывает это предположение?
б) Какой характер будет иметь движение в том случае, если Е/В>с?
в) Пусть разность потенциалов между двумя параллельными пластинами, одна из которых совпадает с плоскостью xz (y=0), а другая находится на расстоянии d (y=d), равна V0=E·d, и между пластинами приложено магнитное поле, параллельное пластинам. Пусть кинетическая энергия электронов, вылетающих из отрицательно заряженной пластины, равна нулю. При каком значении напряженности магнитного поля испущенные электроны не будут достигать другой пластины?
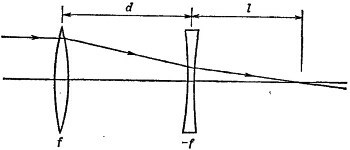 29.4. Принцип фокусировки частиц в неоднородном поле может быть продемонстрирован с помощью следующей оптической модели: 29.4. Принцип фокусировки частиц в неоднородном поле может быть продемонстрирован с помощью следующей оптической модели:
Даже при одинаковых по модулю фокусных расстояниях линз существуют условия, когда такая система будет фокусировать.
а) Определите зависимость / от d для света, падающего вдоль оптической оси.
б) При каких условиях изображение будет реальным, при каких — мнимым?
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




 К главе 15. Векторный потенциал
К главе 15. Векторный потенциал К главе 17. Законы индукции
К главе 17. Законы индукции 17.2. Жесткий провод, согнутый в полукруг радиуса r, вращается с угловой скоростью ω в однородном магнитном поле. Чему равна частота и амплитуда напряжения и тока, наведенного в проводнике, если внутреннее сопротивление вольтметра М равно RM, а сопротивление остальных частей цепи ничтожно? Предположите, что поле, создаваемое током, мало по сравнению с полем В, т. е. наведенный ток мал и неспособен существенно изменить величину В.
17.2. Жесткий провод, согнутый в полукруг радиуса r, вращается с угловой скоростью ω в однородном магнитном поле. Чему равна частота и амплитуда напряжения и тока, наведенного в проводнике, если внутреннее сопротивление вольтметра М равно RM, а сопротивление остальных частей цепи ничтожно? Предположите, что поле, создаваемое током, мало по сравнению с полем В, т. е. наведенный ток мал и неспособен существенно изменить величину В. 17.3. По круговому витку (1) провода, радиус а которого мал, течет постоянный ток /. Другой точно такой же виток провода (2) помещен на оси, проходящей через центр первого витка, на расстоянии R, причем R»a. Плоскости витков параллельны. Затем виток (2) приводится во вращение с угловой скоростью ω вокруг одного из его диаметров. Какова наведенная в цепи витка (2) э. д. с, если он разомкнут?
17.3. По круговому витку (1) провода, радиус а которого мал, течет постоянный ток /. Другой точно такой же виток провода (2) помещен на оси, проходящей через центр первого витка, на расстоянии R, причем R»a. Плоскости витков параллельны. Затем виток (2) приводится во вращение с угловой скоростью ω вокруг одного из его диаметров. Какова наведенная в цепи витка (2) э. д. с, если он разомкнут? 17. 4. Металлический провод массы т скользит без трения по двум параллельным металлическим рельсам, находящимся на расстоянии d друг от друга, как показано на рисунке. При движении провод пересекает силовые линии однородного магнитного поля В, направленного вертикально.
17. 4. Металлический провод массы т скользит без трения по двум параллельным металлическим рельсам, находящимся на расстоянии d друг от друга, как показано на рисунке. При движении провод пересекает силовые линии однородного магнитного поля В, направленного вертикально. 17.6. Кабель сделан из провода и охватывающего его коаксиального проводящего цилиндра, по которому течет ток в противоположном направлении. Радиус внутреннего провода кабеля равен а, а внешний радиус цилиндра равен b.
17.6. Кабель сделан из провода и охватывающего его коаксиального проводящего цилиндра, по которому течет ток в противоположном направлении. Радиус внутреннего провода кабеля равен а, а внешний радиус цилиндра равен b.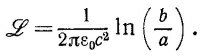
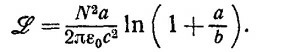
 17.8. Два плоских витка провода с одинаковой площадью А и током / помещены на расстоянии r друг от друга так, как показано на рисунке. Единичные векторы n1 и n2, определяющие направления нормалей к виткам, образуют с линией, соединяющей центры витков, углы α1 и α2 и лежат с ней в одной плоскости.
17.8. Два плоских витка провода с одинаковой площадью А и током / помещены на расстоянии r друг от друга так, как показано на рисунке. Единичные векторы n1 и n2, определяющие направления нормалей к виткам, образуют с линией, соединяющей центры витков, углы α1 и α2 и лежат с ней в одной плоскости. 17.9. Круговой виток провода радиуса r1 расположен в центре соленоида длиной /, состоящего из N витков радиуса r2, причем r2»r1. Оси витка и соленоида совпадают. Обозначив цепь кругового витка индексом 1, а цепь соленоида индексом 2, найдите индуктивности M12 и M21.
17.9. Круговой виток провода радиуса r1 расположен в центре соленоида длиной /, состоящего из N витков радиуса r2, причем r2»r1. Оси витка и соленоида совпадают. Обозначив цепь кругового витка индексом 1, а цепь соленоида индексом 2, найдите индуктивности M12 и M21. 17.10. В однородном магнитном поле В, направленном перпендикулярно плоскости рисунка, по двум проводящим рельсам со скоростью v движется провод. Какой ток течет через сопротивление R, если v = 100 см/сек, /=10 см, В =0,1 вебер/м2 и R=10 ом (магнитным полем, создаваемым током, пренебречь). В какую сторону изменится найденный вами ток, если не пренебрегать полем, создаваемым движущимся проводником? Изменится ли ваш ответ, если магнит, создающий поле В, будет двигаться со скоростью v в ту же сторону, что и провод? Как меняется со временем коэффициент самоиндукции изображенной на рисунке цепи?
17.10. В однородном магнитном поле В, направленном перпендикулярно плоскости рисунка, по двум проводящим рельсам со скоростью v движется провод. Какой ток течет через сопротивление R, если v = 100 см/сек, /=10 см, В =0,1 вебер/м2 и R=10 ом (магнитным полем, создаваемым током, пренебречь). В какую сторону изменится найденный вами ток, если не пренебрегать полем, создаваемым движущимся проводником? Изменится ли ваш ответ, если магнит, создающий поле В, будет двигаться со скоростью v в ту же сторону, что и провод? Как меняется со временем коэффициент самоиндукции изображенной на рисунке цепи? 17.11. Рассмотрим два витка провода радиуса а, находящиеся на расстоянии d друг от друга (d»a). Центры витков лежат на одной прямой, перпендикулярной плоскости обоих витков. Через виток А в направлении, показанном на рисунке стрелкой, пропускается ток /=K0t2 (t — время). Сопротивление витка Б равно R.
17.11. Рассмотрим два витка провода радиуса а, находящиеся на расстоянии d друг от друга (d»a). Центры витков лежат на одной прямой, перпендикулярной плоскости обоих витков. Через виток А в направлении, показанном на рисунке стрелкой, пропускается ток /=K0t2 (t — время). Сопротивление витка Б равно R.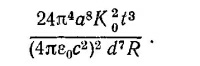
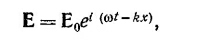
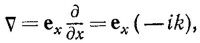
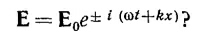
 21.2. С помощью уравнения (21.1) (см. вып. 6, стр. 142) можно найти электрическое поле, создаваемое движущимся зарядом. Рассмотрим диполь, образованный положительным и отрицательным зарядами, осциллирующими относительно начала координат вдоль оси z так, что координата положительного заряда меняется со временем по закону z+=d/2cosω t, а отрицательного z_=–d/2cosω t, Дипольный момент такой системы зарядов равен p=dez dcosω t. Покажите, что электрическое поле диполя, найденное из упомянутого уравнения, имеет вид
21.2. С помощью уравнения (21.1) (см. вып. 6, стр. 142) можно найти электрическое поле, создаваемое движущимся зарядом. Рассмотрим диполь, образованный положительным и отрицательным зарядами, осциллирующими относительно начала координат вдоль оси z так, что координата положительного заряда меняется со временем по закону z+=d/2cosω t, а отрицательного z_=–d/2cosω t, Дипольный момент такой системы зарядов равен p=dez dcosω t. Покажите, что электрическое поле диполя, найденное из упомянутого уравнения, имеет вид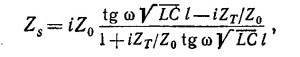
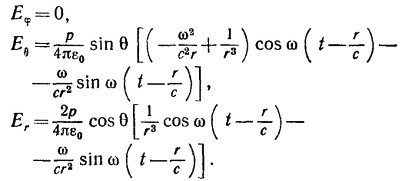
 21.4. В задаче 21.2 диполь состоял из двух зарядов, осциллирующих вокруг начала координат. Диполь, величина которого изменяется со временем по гармоническому закону, можно построить иным способом: взять два проводящих шара, соединить их проводником длиной d и по проводнику пропустить переменный ток. Тогда на концах проводника возникает переменный заряд ±q(t), a сам проводник остается в целом нейтральным; заряд q(t) можно рассматривать как вещественную часть выражения Q0e¡ωt.
21.4. В задаче 21.2 диполь состоял из двух зарядов, осциллирующих вокруг начала координат. Диполь, величина которого изменяется со временем по гармоническому закону, можно построить иным способом: взять два проводящих шара, соединить их проводником длиной d и по проводнику пропустить переменный ток. Тогда на концах проводника возникает переменный заряд ±q(t), a сам проводник остается в целом нейтральным; заряд q(t) можно рассматривать как вещественную часть выражения Q0e¡ωt.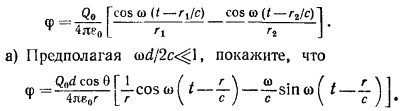
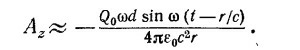
 21.5. Антенна, предназначенная для работы на частоте ω=2πс/λ, изготовлена из двух колинеарных проводов, длина каждого из которых равна 1/4 длины волны. На антенну подается синусоидальное меняющееся напряжение требуемой частоты. Возникающее в антенне распределение токов с большой степенью точности описывается выражением
21.5. Антенна, предназначенная для работы на частоте ω=2πс/λ, изготовлена из двух колинеарных проводов, длина каждого из которых равна 1/4 длины волны. На антенну подается синусоидальное меняющееся напряжение требуемой частоты. Возникающее в антенне распределение токов с большой степенью точности описывается выражением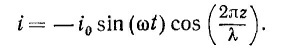
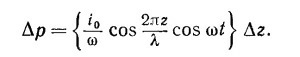
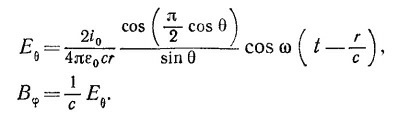
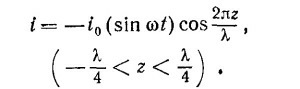
 21.6. Частица с зарядом со скоростью v.
21.6. Частица с зарядом со скоростью v. 22.2. а) Найдите ток / в цепи, схема которой изображена на рисунке.
22.2. а) Найдите ток / в цепи, схема которой изображена на рисунке. 22.3. Принципиальная схема устройства высокой точности звуковоспроизведения имеет такой вид, как изображено на рисунке. Эффективное сопротивление каждого громкоговорителя равно R.
22.3. Принципиальная схема устройства высокой точности звуковоспроизведения имеет такой вид, как изображено на рисунке. Эффективное сопротивление каждого громкоговорителя равно R. 22.4. Покажите, что амплитуда разности потенциалов (напряжение) между точками а и b цепи, изображенной на схеме, не зависит от ω. Опишите качественно зависимость фазы этой разности потенциалов от частоты ω. Как изменится величина разности потенциалов между точками а и b, а также фаза, если источник напряжения обладает внутренним сопротивлением R10/?
22.4. Покажите, что амплитуда разности потенциалов (напряжение) между точками а и b цепи, изображенной на схеме, не зависит от ω. Опишите качественно зависимость фазы этой разности потенциалов от частоты ω. Как изменится величина разности потенциалов между точками а и b, а также фаза, если источник напряжения обладает внутренним сопротивлением R10/? 22.5. Электрическая цепь имеет вид, изображенный на схеме.
22.5. Электрическая цепь имеет вид, изображенный на схеме. 22.6. Мостовая схема, изображенная на рисунке, используется для измерений индуктивности. Источником переменной э. д. с. частоты ω служит генератор напряжения. Если мост сбалансирован, ток через детектор RD равен нулю. Найдите L как функцию R и С.
22.6. Мостовая схема, изображенная на рисунке, используется для измерений индуктивности. Источником переменной э. д. с. частоты ω служит генератор напряжения. Если мост сбалансирован, ток через детектор RD равен нулю. Найдите L как функцию R и С. 22.7. Изображенная схема представляет собой мост Вейна, часто используемый в RС-цепях. Если ток через детектор равен нулю, говорят, что мост сбалансирован. Покажите, что баланс наступает при одновременном выполнении следующих двух условий:
22.7. Изображенная схема представляет собой мост Вейна, часто используемый в RС-цепях. Если ток через детектор равен нулю, говорят, что мост сбалансирован. Покажите, что баланс наступает при одновременном выполнении следующих двух условий: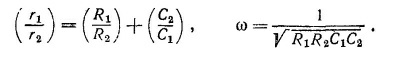
 22.8. В цепи, изображенной на рисунке, действует источник переменного напряжения V(t)=V0cosωt.
22.8. В цепи, изображенной на рисунке, действует источник переменного напряжения V(t)=V0cosωt.  22.9. Электрическая цепь собрана так, что один ее свободный конец, изображенный на рисунке стрелкой, упирающейся в точку Р3, может быть присоединен к любой из точек Р0, Ри1 ..., Рn.
22.9. Электрическая цепь собрана так, что один ее свободный конец, изображенный на рисунке стрелкой, упирающейся в точку Р3, может быть присоединен к любой из точек Р0, Ри1 ..., Рn. К главе 23. Полые резонаторы
К главе 23. Полые резонаторы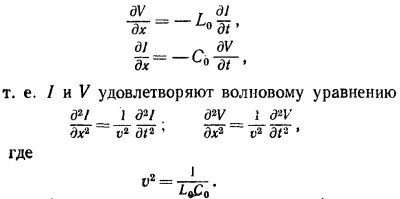
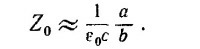
 24.4. Волновод в форме прямоугольного параллелепипеда (стороны сечения а и b) изготовлен из идеального проводящего материала. Концы одной секции волновода, длина которой /, закрыты пластинами из проводящего материала, так что полость внутри волновода фактически представляет собой резонатор. Если электрическое поле в полости определяется вещественной частью выражения
24.4. Волновод в форме прямоугольного параллелепипеда (стороны сечения а и b) изготовлен из идеального проводящего материала. Концы одной секции волновода, длина которой /, закрыты пластинами из проводящего материала, так что полость внутри волновода фактически представляет собой резонатор. Если электрическое поле в полости определяется вещественной частью выражения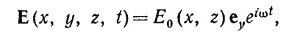
 24.6. Покажите, что если при х=l линия передачи замкнута (включен элемент с импедансом ZT), to импеданс на «входе» линии (х=0) равен
24.6. Покажите, что если при х=l линия передачи замкнута (включен элемент с импедансом ZT), to импеданс на «входе» линии (х=0) равен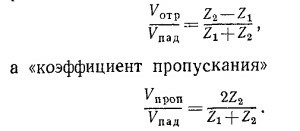
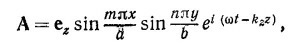
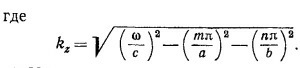
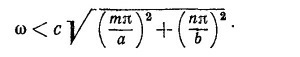
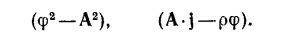
 25.2. Комптон-эффект состоит в том, что фотон, налетая на покоящийся электрон, рассеивается на нем, как частица на частице. Выразите энергию рассеянного фотона через энергию падающего фотона и угол отклонения его направления распространения от первоначального.
25.2. Комптон-эффект состоит в том, что фотон, налетая на покоящийся электрон, рассеивается на нем, как частица на частице. Выразите энергию рассеянного фотона через энергию падающего фотона и угол отклонения его направления распространения от первоначального.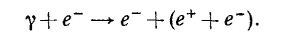
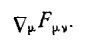
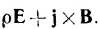
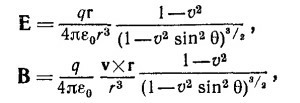
 26.8. Два электрона с одинаковой скоростью v движутся параллельно друг другу по обе стороны от бесконечной положительно заряженной плоскости на расстоянии а от нее; плотность покоящихся поверхностных зарядов равна σ.
26.8. Два электрона с одинаковой скоростью v движутся параллельно друг другу по обе стороны от бесконечной положительно заряженной плоскости на расстоянии а от нее; плотность покоящихся поверхностных зарядов равна σ.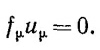
 26.10. Частица с зарядом q движется с постоянной скоростью в плоскости ху вдоль траектории, изображенной на рисунке пунктирной линией (в начале координат частица рассеивается). Величина скорости частицы вдоль всей траектории остается постоянной. В момент времени t= t1 частица находится в точке х=а, у=0.
26.10. Частица с зарядом q движется с постоянной скоростью в плоскости ху вдоль траектории, изображенной на рисунке пунктирной линией (в начале координат частица рассеивается). Величина скорости частицы вдоль всей траектории остается постоянной. В момент времени t= t1 частица находится в точке х=а, у=0.
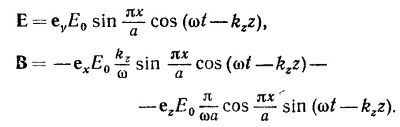
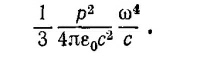
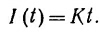

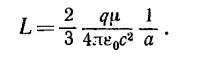
 29.4. Принцип фокусировки частиц в неоднородном поле может быть продемонстрирован с помощью следующей оптической модели:
29.4. Принцип фокусировки частиц в неоднородном поле может быть продемонстрирован с помощью следующей оптической модели: