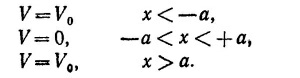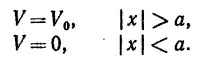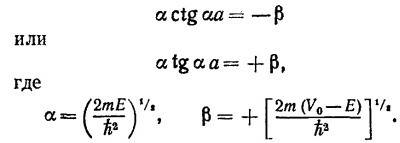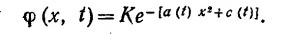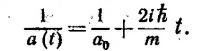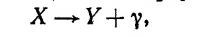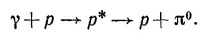Главная >> Фейнмановские лекции по физике >> Том 10 >> Задачи к томам VIII-IX 9. Квантовая механика (II)
11.1. Рассмотрим бесконечную цепочку атомов, расположенных друг от друга на равных расстояниях b (координата атома n равна х =bn), и предположим, что электрон может находиться в каждом из атомов в двух состояниях i и j с различными энергиями Е¡ и Ej, т. е. набор базисных состояний можно записать следующим образом:
| электрон на атоме хn в состоянии ¡> = |xn, ¡>,
| электрон на атоме хn в состоянии j> = |xn, j>.
Предположим далее, что электрон может перескакивать со своего атома на ближайший соседний с амплитудами:
Рассмотрим случай, когда А¡j=Аj¡=В и Аjj=А¡¡=А. С помощью процедуры, описанной в гл. 11 «Лекций», найдите допустимые значения энергии такой системы. Опишите зонную структуру в предельных случаях |E¡—Ej|«2В и |E¡—Ej|»2B. Сравните свой ответ с решением, найденным в гл. 11.
11. 2. Рассмотрим бесконечную цепочку, состоящую из атомов двух типов а и b:
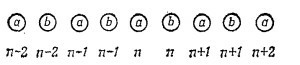 |
Пусть амплитуда обнаружения электрона на n-м атоме типа а будет Саn, а на n-м атоме типа b — будет Сbn. Предположим, что энергия электрона в атоме а равна Е0+ ΔЕ, а в атоме b равна Е0– ΔЕ; допустим еще, что матричный элемент гамильтониана для перехода между ближайшими соседями равен —А. Расстояние между атомами равно с. Рассчитайте и приближенно начертите график зависимости энергии стационарного состояния от волнового числа k. (Для каждого заданного значения k получатся два значения энергии.) Какие ограничения следует наложить на значения k, чтобы учесть каждое состояние ровно один раз?
11.3. Рассмотрим рассеяние на примеси (см. пример, приведенный в гл. 11, вып. 9). Пусть атом под номером n=0 отличается от всех остальных. Положим H00=E0, H01=H10=H0(_1)=H(_1)0=–В, где В≠А. Найдите β и γ и убедитесь в том, что | β |2+ | γ |2= 1.
11.4. В предыдущей задаче, как и в примере, приведенном в гл. 11 (вып. 9), β=γ—1. Легко проверить также, что в любом более общем случае, являющемся комбинацией этих двух, равенство β=γ—1 также справедливо.
Следовательно, в общем случае одномерного рассеяния существует «закон сохранения числа частиц»
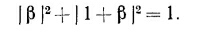 |
а) Покажите, что для его выполнения необходимо, чтобы
б) Покажите, что β можно записать следующим образом:
где η — вещественное число. Величина η называется «сдвигом фазы при рассеянии» и содержит информацию как о фазе, так и об амплитуде рассеянной волны. (Это утверждение в трехмерном случае справедливо так же, как и в одномерном.)
 11.5. Рассмотрим одномерный аналог поверхности раздела, где бесконечный кристалл претерпевает изменение своих свойств. Пусть частица падает слева, как в гл. 11. Пусть в области / значения параметров равны Е0, —А, b, а в области // равны Е′0, —А′, b′. Аналог амплитуд А и А′ для атомов, расположенных по обе стороны линии раздела, обозначим буквой В. Предположим, что А, А′ и В — вещественные числа. 11.5. Рассмотрим одномерный аналог поверхности раздела, где бесконечный кристалл претерпевает изменение своих свойств. Пусть частица падает слева, как в гл. 11. Пусть в области / значения параметров равны Е0, —А, b, а в области // равны Е′0, —А′, b′. Аналог амплитуд А и А′ для атомов, расположенных по обе стороны линии раздела, обозначим буквой В. Предположим, что А, А′ и В — вещественные числа.
а) Покажите, что γ=B/A′ (1+β) в разрыве между атомами n=0 и n=+1.
б) Выразите β через А, А′, В, kb, k′b′.
Покажите, что |β|=1 при мнимом (k′b′). Каков физический смысл этого результата? При каких значениях (Е—Е′0) получается полное отражение?
в) Проверьте закон сохранения числа частиц, показав, что
где vg и v′g — групповые скорости в разных областях. Как вы объясните появление множителя при |γ|2?
К главе 12. Полупроводники
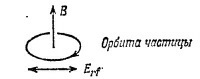 12.1. Ниже приведена обычная схема проведения экспериментов по циклотронному резонансу. 12.1. Ниже приведена обычная схема проведения экспериментов по циклотронному резонансу.
В= Во — статическое магнитное поле, направленное по оси z. Переменное электрическое поле E=E0cosωt направлено по оси х.
Частота циклотронного резонанса ωс определяется по максимуму поглощаемой мощности поля Е. Элементарное решение задачи о движении частицы в однородном магнитном поле дает
где m* — эффективная масса. Предположим, что эффективная масса не зависит от направления, по которому движется частица.
Уравнение движения электрона (или дырки) в полупроводнике имеет вид
где т — среднее время между столкновениями (см. «Лекции», вып. 7, гл. 32).
Пусть vх=vое¡ωt, a Ex=E0e¡ωt. Покажите, что
Поглощаемая мощность пропорциональна Re, [vx/Ex]. Почему? Как получить сразу обе величины т и m* из данных по циклотронному резонансу? Обратите внимание на то, что для наблюдения резонанса необходимо, чтобы ωcт >1. Что это означает физически?
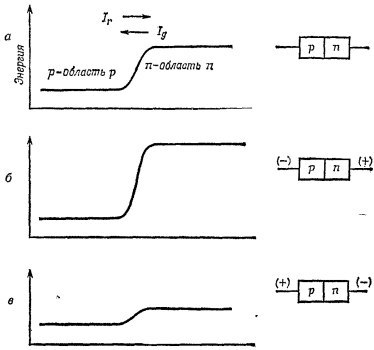
12. 2. На рисунке (стр. 542) показана типичная энергетическая диаграмма для дырок в р — n-переходе (например, в полупроводниковом диоде) в отсутствие внешнего напряжения. В равновесном состоянии в этом случае имеется ток «тепловых дырок» /g.Эти дырки диффундируют из области n в область р, и «ток рождения» в точности равен «току рекомбинации дырок» Ir который течет из области р в область n. Если приложить «обратное напряжение» или «прямое напряжение» к р — n-переходу, то энергетическая диаграмма изменится (см. фиг. б и в). Рассмотрите эти три случая и покажите, что выражение для результирующего дырочного тока имеет вид
А какое выражение получится для полного тока? (V — напряжение, приложенное к р — n-переходу.)
К главе 13. Приближение независимых частиц
13.1. Структуру молекулы бутадиена можно изобразить следующим образом:
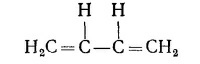 |
Мысленно удалим четыре электрона, осуществляющие двойные связи, а затем будем добавлять их по одному. Такую задачу можно рассматривать с помощью модели независимых частиц. В частности, эту систему можно рассматривать как совокупность четырех потенциальных ям с энергиями E0 и матричными элементами гамильтониана — А. Чему равна длина волны излучения, испускаемого молекулами бутадиена при переходе с первого возбужденного уровня на основной? Считайте, что А = 1 эв. В однократно ионизованной молекуле бутадиена имеется только три электрона из двойных связей. Что вы можете сказать о распределении этих электронов в молекуле?
13.2. Нужно оценить энергию, необходимую для разрыва бензольного кольца, и рассчитать разность энергий двух конфигураций, показанных на рисунке. Используйте для этой оценки теорию молекулярных орбит в приближении независимых частиц. Ответ выразите в эв на молекулу, используя тот факт, что
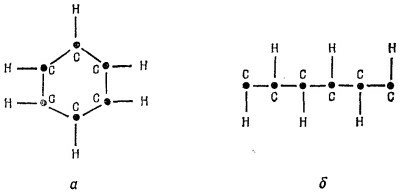 |
при переходе с первого возбужденного состояния на основное молекулы бензола испускают излучение с длиной волны 2000 Å.
13.3. К ферромагнитному веществу при очень низких температурах применимы те рассуждения о спиновых волнах, которые приведены в гл. 13 «Лекций» (вып. 9). В частности, для любого состояния К с энергией ЕK≈К2b2А существует определенная вероятность (ее можно найти из термодинамических соображений) обнаружить несколько атомов в состояниях «спином вниз», если при нулевой температуре все атомы находились в состояниях «спином вверх». Покажите, что среднее число атомов со спинами, направленными вниз, пропорционально 1\еЕк/кТ — 1. Если распространить эти рассуждения на трехмерный случай, то ЕК≈Аb2(Кx2+Ку2+Кz2) и полное число атомов «спином вниз» в единице объема определяется выражением
Докажите это. В пределе при Т→0 намагниченность выходит на насыщение и принимает значение Мнасыщ. Покажите, что при низких температурах справедлив закон
Вычислите интеграл, разложив подынтегральное выражение в ряд.
К главе 14. Зависимость амплитуд от места
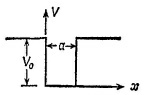 14.1. Рассмотрим одномерное движение частицы с массой т в прямоугольной потенциальной яме. Для простоты предположим, что V0→∞. 14.1. Рассмотрим одномерное движение частицы с массой т в прямоугольной потенциальной яме. Для простоты предположим, что V0→∞.
а) В стационарном состоянии с наименьшей энергией Ео: ψ0(x,t)=u0(x)e–¡E0t/h.
Мы должны считать, что и0(х)=0 во всех точках вне ямы (т. е. уже при х=—ε или х=а+ε). Почему?
б) Решите уравнение Шредингера внутри ямы, используя граничное условие, приведенное в пункте (а). Найдите Е0 и изобразите зависимость и0(х). Нормировать и0 (х) не нужно.
в) Найдите разность энергий первого возбужденного и основного состояний.
г) Для самого нижнего состояния изобразите грубо вероятность обнаружить у частицы значение импульса в интервале от р до p+dp. Точного интегрирования не требуется, о нормировке тоже не беспокойтесь. Но масштаб по оси импульсов укажите.
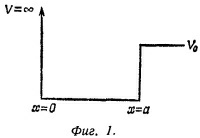 14.2. Рассмотрим движение частицы с массой m в одномерной потенциальной яме, которая изображена на фиг. 1. 14.2. Рассмотрим движение частицы с массой m в одномерной потенциальной яме, которая изображена на фиг. 1.
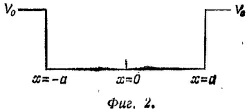 а) Найдите такое значение V0, при котором энергия частицы в основном состоянии отличается на 10% от энергии основного состояния при V0→∞. а) Найдите такое значение V0, при котором энергия частицы в основном состоянии отличается на 10% от энергии основного состояния при V0→∞.
б) Пусть V0— значение, найденное в пункте (а). Не пускаясь в длинные вычисления, найдите энергию первого возбужденного состояния в яме, изображенной на фиг. 2 и определяемой следующими условиями:
14.3. Рассмотрим следующую одномерную задачу. Частица массы т находится в прямоугольной потенциальной яме:
Ниже приведены два равенства. Покажите, что их можно получить, потребовав, чтобы волновые функции, являющиеся решениями уравнения Шредингера, удовлетворяли необходимым граничным условиям. Речь идет о таких равенствах:
Если V0a2=4h2/2m, оцените значения энергии основного и первого возбужденного состояний. Нанесите на график волновые функции этих состояний. Сколько всего существует связанных состояний, если V0a2<(π2h2/8m)?
14.4. В гл. 14 «Лекций» (вып. 9) был найден разброс по импульсам для случая, когда волновая функция имеет гауссову форму. В общем случае, однако, пространственная протяженность волнового пакета не останется постоянной, а будет увеличиваться:
Используя уравнение Шредингера, покажите, что для свободной частицы
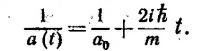 |
Чему равно c(t)? Если волновая функция описывает электрон, первоначально находившийся внутри области шириной 1 Å, то какова будет ширина этой «области локализации» через 1 сек? Преобразуем волновую функцию в импульсное представление, т. е. найдем вероятность обнаружения частицы с заданным значением импульса р. Как изменяется со временем ширина распределения вероятностей для импульсов? Покажите, что найденный таким образом «разброс по импульсам» согласуется с «разбросом по скоростям», который можно непосредственно получить из временной зависимости координатной волновой функции.
К главе 16. Момент количества движения
16.1. Некоторое возбужденное состояние атома имеет спин 1 и может «разрядиться», испустив фотон и перейдя в состояние со спином, равным нулю. Рассмотрим возбужденный атом, у которого проекция момента на ось z равна нулю. Пусть A(θ) — амплитуда испускания фотона с правой круговой поляризацией в малый интервал телесных углов ΔΩ в направлении, образующем с осью z угол θ. Как A(θ) зависит от θ?
16.2. Частица X, имеющая спин 1/2, распадается по схеме
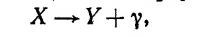 |
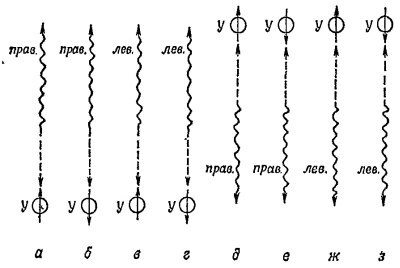
где частица Y имеет спин 1/2 и положительную четность. Если спин частицы X направлен вдоль оси z, то продукты распада, движущиеся вдоль оси z, могут поручаться в восьми состояниях, представленных на рисунке (стр. 548). Волнистая и штрихованная линии со стрелками указывают соответственно направление движений фотона и частицы Y, а стрелка у Υ — направление спина этой частицы.
а) Какие амплитуды конечных состояний обязательно равны нулю?
б) Рассчитайте угловое распределение частиц Y, поляризованных вдоль направления своего движения, если распадающиеся частицы X поляризованы вдоль оси z.
в) Рассчитайте угловое распределение всех частиц Y независимо от их поляризации.
г) Тщательные эксперименты не обнаружили в этом распаде каких-либо отклонений от изотропного углового распределения. Какой физической причиной это можно объяснить?
16.3. На синхротроне исследуется реакция
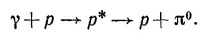 |
Значком р* обозначено возбужденное состояние протона, которое распадается на протон и π0-мезон. Известно, что в определенном интервале энергий фотона состояние р* имеет полный момент 3/2. Предположим, что пучок фотонов, обладающих правой круговой поляризацией и энергией, лежащей в упомянутом интервале, падает вдоль оси z на мишень, состоящую из неполяризованных протонов. Угловое распределение этой реакции можно анализировать, рассуждая следующим образом. Фотон и протон образуют р* в состоянии |j=3/2, m=+1/2> с амплитудой а и в состоянии |3/2, +3/2> — с амплитудой b. Возбужденное состояние распадается на π0-мезон с нулевым спином и протон, движущиеся в противоположных направлениях. Пусть f — амплитуда вылета протона вдоль оси z со спином, направленным вверх, a g — со спином, направленным вниз.
Объясните, почему для состояния р* разрешенными являются только значения m=+3/2 и m=+1/2, a для конечного состояния — только значения m′=+1/2 и т′=—1/2 (т′ обозначает проекцию на направление испускания). Выразите угловое распределение π0-мезонов через а, b и θ. Полагайте f=g.
16. 4. Рассмотрим упругое рассеяние π+-мезонов на неполяризованной протонной мишени. Мезоны имеют спин 0; четность сохраняется. Предполагается, что в рассеянии доминирует процесс, при котором протон переходит в возбужденное состояние с j=3/2, поглощая мезон. (Момент j=3/2 получается за счет сложения спина протона и орбитального момента.) Затем мезон испускается снова, а протон переходит в основное состояние. Покажите, что из такого предположения следует угловое распределение рассеянных мезонов, пропорциональное (1+3cos2θ).
16.5. Основное состояние атома имеет спин, равный нулю, и положительную четность. Спин первого возбужденного состояния равен единице, а четность неизвестна. Пусть некоторое количество атомов находится в первом возбужденном состоянии, и все они имеют проекцию момента т=1 на ось z. Рассмотрим фотоны, которые испускаются этими атомами при переходе в основное состояние.
а) Можно ли определить четность возбужденного состояния, если измерять угловое распределение испускаемых фотонов, не обращая внимания на их поляризацию?
б) Покажите, что эту неизвестную четность можно определить, измеряя угловые распределения фотонов, поляризованных вдоль направлений х′ и у′ (Ось z′ выбирается в направлении движения фотона и располагается в плоскости х — z.)
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




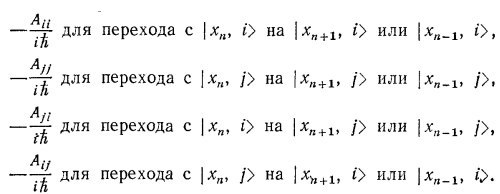

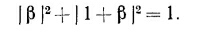
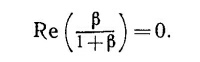
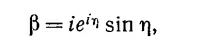
 11.5. Рассмотрим одномерный аналог поверхности раздела, где бесконечный кристалл претерпевает изменение своих свойств. Пусть частица падает слева, как в гл. 11. Пусть в области / значения параметров равны Е0, —А, b, а в области // равны Е′0, —А′, b′. Аналог амплитуд А и А′ для атомов, расположенных по обе стороны линии раздела, обозначим буквой В. Предположим, что А, А′ и В — вещественные числа.
11.5. Рассмотрим одномерный аналог поверхности раздела, где бесконечный кристалл претерпевает изменение своих свойств. Пусть частица падает слева, как в гл. 11. Пусть в области / значения параметров равны Е0, —А, b, а в области // равны Е′0, —А′, b′. Аналог амплитуд А и А′ для атомов, расположенных по обе стороны линии раздела, обозначим буквой В. Предположим, что А, А′ и В — вещественные числа.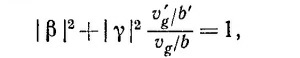
 12.1. Ниже приведена обычная схема проведения экспериментов по циклотронному резонансу.
12.1. Ниже приведена обычная схема проведения экспериментов по циклотронному резонансу.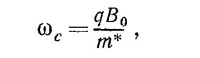
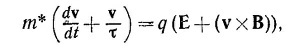
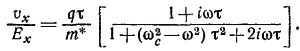
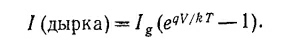
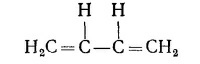

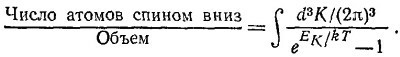
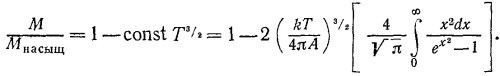
 14.1. Рассмотрим одномерное движение частицы с массой т в прямоугольной потенциальной яме. Для простоты предположим, что V0→∞.
14.1. Рассмотрим одномерное движение частицы с массой т в прямоугольной потенциальной яме. Для простоты предположим, что V0→∞. 14.2. Рассмотрим движение частицы с массой m в одномерной потенциальной яме, которая изображена на фиг. 1.
14.2. Рассмотрим движение частицы с массой m в одномерной потенциальной яме, которая изображена на фиг. 1.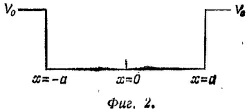 а) Найдите такое значение V0, при котором энергия частицы в основном состоянии отличается на 10% от энергии основного состояния при V0→∞.
а) Найдите такое значение V0, при котором энергия частицы в основном состоянии отличается на 10% от энергии основного состояния при V0→∞.