Главная >> Фейнмановские лекции по физике >> Том 10 >> Задачи к томам I-IV Решения и ответы
1 СОВРЕМЕННАЯ НАУКА О ПРИРОДЕ • ЗАКОНЫ МЕХАНИКИ
К главе 1. Атомы в движении
1.1. а) Известно, что при нормальных условиях грамм-молекула любого вещества содержит А молекул (А =6,02·1023 — число Авогадро) и занимает в газообразном состоянии объем vo = 22,4 л = 22400 см3. Следовательно, в 1 см3 газообразного воздуха содержится nB «молекул»:
Плотность газообразного и жидкого воздуха равна соответственно
где т — масса «молекулы» воздуха, а nж — число «молекул» в 1 см3 жидкого воздуха, поэтому
б) Зная плотность воздуха, вычисляем массу «молекулы» воздуха
в) Представим себе молекулу воздуха в виде твердого шарика с радиусом r. Ясно, что молекулы столкнутся, если их центры подойдут на расстояние, меньшее или равное 2r. За единицу времени молекула пролетает путь, равный ее средней скорости v. При этом она сталкивается со всеми молекулами, центры которых окажутся в «захватываемом» ею объеме π (2r)2 v, т. е. испытывает 4πr2n0v столкновений (n0—число молекул в 1 см3 воздуха при нормальных условиях).
Считая для оценки, что между двумя последовательными столкновениями молекула проходит равные расстояния λ (это и есть длина свободного пробега) и что все молекулы одинаковы, находим
Полагая r≈ 10–8 см, получаем λ = 3,2·10–5 см. От давления зависит только число частиц в 1 см3, которое просто пропорционально давлению, так что можно написать n = ср (с—коэффициент пропорциональности) и λ=1/(4πr2cр), откуда λp = const. Поэтому для длины свободного пробега молекулы при разных давлениях, но одинаковой температуре газа имеем
Таким образом, давление, при котором длина свободного пробега составляет 1 м, равно
1.2. Предположим, что объем древней капли был равен примерно 1 см3, т. е. что капля содержала около N ≈3·1022 молекул. Естественно предположить, что за огромный промежуток времени, прошедший от палеозойской эры до наших дней, молекулы капли равномерно распределились по всей имеющейся на Земле воде. В этом случае студент-геолог проглотил n = (v/V) N молекул нашей капли, где v — объем выпитой им воды, а V—объем всей воды на Земле. Оценим V.
Будем считать, что вода покрывает равномерно весь земной шар слоем толщиной d ≈ 3 км. В этом случае
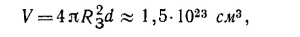 |
где RЗ—радиус Земли. Положив v =150 см3 (три четверти стакана), получим n ≈30.
1.3. Рассмотрим сначала, как будет происходить испарение, если стакан накрыть крышкой и откачать из-под нее весь воздух. Пока водяного пара под крышкой мало, жидкость будет испаряться. Из воды все время будут вылетать молекулы воды, а из пара какое-то число молекул будет возвращаться в воду, т. е. конденсироваться. Через некоторое время в стакане установится динамическое равновесие: число вылетающих из воды молекул станет равным числу возвращающихся обратно. Если убрать крышку, вода
начнет непрерывно испаряться, причем число вылетающих молекул будет таким же, как и тогда, когда стакан был накрыт, ведь процесс испарения зависит только от движения молекул в воде, число же возвращающихся в воду молекул зависит от количества водяных паров в воздухе над стаканом.
Оценим количество вылетающих из воды молекул в единицу времени при равновесии. Проще вычислять не это число, а равное ему число конденсирующихся молекул пара.
Пусть в единице объема воздуха над крышкой содержится n молекул водяного пара. Число n зависит только от температуры воздуха, оно измерено экспериментально; существуют таблицы зависимости n от температуры. За промежуток времени t поверхности воды достигнут только те молекулы пара (скорость молекулы v), которые находились в начальный момент времени не дальше, чем vBt (vB — вертикальная скорость молекулы). Другими словами, поверхности воды достигают те молекулы, которые находятся в объеме SvBt над стаканом (S—площадь поперечного сечения стакана). Следовательно, в единицу временя конденсируется 1/2nSv молекул пара.
Как уже отмечалось, число испаряющихся молекул при снятой крышке будет таким же, как и при закрытой крышке. Но число конденсирующихся молекул зависит от того, сколько молекул пара содержится в единице объема воздуха над поверхностью жидкости. Будем считать, что влажность воздуха близка к нормальной.
Влажностью (относительной) называют отношение числа содержащихся в воздухе молекул водяного пара в данный момент времени к максимально возможному (т. е. числу молекул пара в единице объема при равновесии). Нормальной считается влажность около 60 — 80%. Мы положим, что влажность воздуха 50%, т. е. в единице объема воздуха содержится n/2 молекул водяного пара. В этом случае, как следует из предыдущего рассмотрения, в воду из пара должно конденсироваться 1/4 nSv молекул. Однако так было бы лишь при условии, что над водой находятся только водяные пары, а не смесь воздуха с паром. При наличии воздуха молекулы из воды отлетают без столкновений только на длину свободного пробега λ (это расстояние ~ 3·10–5 см, см. задачу 1.1), дальше они движутся от поверхности жидкости с очень малой скоростью (по сравнению с тепловой). Поэтому число конденсирующихся молекул определяется не плотностью пара на большом расстоянии от воды, а плотностью пара на расстоянии длины свободного пробега. Считая, что плотность пара в перпендикулярном к поверхности воды направлении меняется линейно, а на расстоянии примерно 1 см она равна уже n/2, находим, что плотность водяных паров на расстоянии λ примерно равна
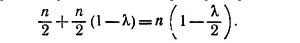 |
Таким образом, с поверхности воды в единицу времени испаряется около nλSv/4 молекул воды. После этого рассмотрения мы можем ответить на поставленные в задаче вопросы.
а) В стакане воды содержится nBSh молекул воды, где nB = 3·1022 см–3—число молекул воды в 1 см3 (см. предыдущую задачу), a h—высота стакана, которую примем равной 10 см. Вся вода испарится за время
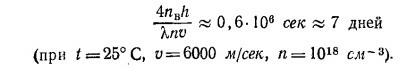 |
б) С площадки в 1 см2 каждую секунду испаряется nλv/4 ≈2·1018 молекул.
в) В среднем за год должно испариться количество воды, равное среднегодовому количеству осадков. Конечно, полученное нами число в пункте (а) превышает количество осадков, так как для расчетов мы выбрали такие условия атмосферы, когда преобладает процесс испарения.
1.4. Хотя атомы и находятся в непрерывном движении, это еще не означает, что они в среднем изменяют свое относительное расположение. В частности, атом, колеблющийся около своего места в кристаллической решетке, в среднем покоится в нем, так что кристаллические тела не меняют своей формы до тех пор, пока амплитуда колебания составляющих их частиц мала по сравнению с расстояниями между ближайшими атомами. При достаточно сильном нагревании эта амплитуда становится столь большой, что
атомы уже больше не «привязаны» к определенному месту, наступает процесс плавления и твердое тело меняет форму.
 1.5. Рассмотрим часть грани кристалла. Расположение атомов в кристалле таково, что каждый атом окружен определенным образом расположенными другими атомами. Это означает, что атомы одного сорта расположены в так называемых эквивалентных точках, т. е, точках, окружение которых совершенно одинаково. Минимальное расстояние между эквивалентными точками а называется периодом решетки. 1.5. Рассмотрим часть грани кристалла. Расположение атомов в кристалле таково, что каждый атом окружен определенным образом расположенными другими атомами. Это означает, что атомы одного сорта расположены в так называемых эквивалентных точках, т. е, точках, окружение которых совершенно одинаково. Минимальное расстояние между эквивалентными точками а называется периодом решетки.
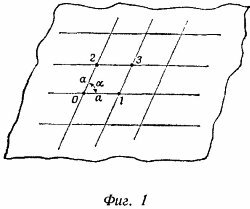
На фиг. 1 эквивалентные точки—это точки 0, 1, 2, 3.
Ближайшие эквивалентные точки образуют некоторую плоскую фигуру — «ячейку» (на рисунке это ромб с вершинами в точках 0, 1, 2, 3), а если рассматривать весь кристалл, а не его грани, то объемную фигуру. При формировании кристалла нарастает все больше и больше ячеек, поэтому форма грани кристалла зависит от геометрической формы ячейки. Разумеется, скорость роста кристалла в разных направлениях различна, так что внешние грани кристалла не являются просто повторением формы ячейки. Но совершенно ясно, что углы между сторонами грани кристалла равны углам между сторонами ячейки, поэтому для ответа на поставленный в задаче вопрос нам достаточно указать, что не может существовать ячеек в форме правильного пятиугольника.
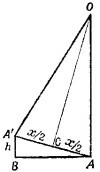
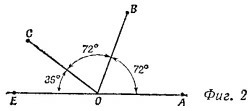 Приведем доказательство от противного. Пусть ячейка кристалла—правильный пятиугольник, а О и А—эквивалентные точки (фиг. 2). Очевидно, эквивалентной должна быть и точка Е (если эквивалентная точка помещается на расстоянии а от О при перемещении вправо, то должна быть эквивалентная точка и при перемещении влево на то же расстояние). Другие эквивалентные точки можно построить, поворачивая отрезок О А на угол 2π/5 = 72°. После первого поворота получим точку В, а после второго—точку С. Но расстояние ЕС < а, что противоречит исходному предположению (расстояние между эквивалентными точками не меньше, чем а). Таким образом, грань кристалла не может быть правильным пятиугольником. Можно строго показать, что аналогичное построение непротиворечиво только в том случае, если ячейки кристалла имеют форму правильного треугольника, четырехугольника (квадрата) и шестиугольника. Приведем доказательство от противного. Пусть ячейка кристалла—правильный пятиугольник, а О и А—эквивалентные точки (фиг. 2). Очевидно, эквивалентной должна быть и точка Е (если эквивалентная точка помещается на расстоянии а от О при перемещении вправо, то должна быть эквивалентная точка и при перемещении влево на то же расстояние). Другие эквивалентные точки можно построить, поворачивая отрезок О А на угол 2π/5 = 72°. После первого поворота получим точку В, а после второго—точку С. Но расстояние ЕС < а, что противоречит исходному предположению (расстояние между эквивалентными точками не меньше, чем а). Таким образом, грань кристалла не может быть правильным пятиугольником. Можно строго показать, что аналогичное построение непротиворечиво только в том случае, если ячейки кристалла имеют форму правильного треугольника, четырехугольника (квадрата) и шестиугольника.
1.6. Беспрерывно ударяясь о стенки сосуда, молекулы газа действуют на них с некоторой силой. Действительно, если сделать одну из стенок сосуда подвижной, то, чтобы удержать ее под градом ударов молекул в неизменном положении, нужно приложить к ней определенную силу. Величина этой силы, отнесенная к единице площади стенки, и есть давление газа. Понятно, что давление будет тем больше, чем больше молекул ударяется о единичную площадку поверхности стенки и чем энергичнее каждый удар. Если плотность газа не особенно велика, то число ударяющихся о стенку молекул просто пропорционально плотности. Сила же удара молекулы о поршень зависит от скорости молекулы: чем быстрее движется молекула, тем сильнее она наносит удар. С другой стороны, понятно, что при данной плотности газа к поршню подлетает и ударяется о него тем больше молекул, чем больше их скорость. Таким образом, мы видим, что от скорости молекул зависит и число ударов о поршень, и сила удара. Поэтому зависимость давления газа от средней скорости молекул—нелинейная. Точный расчет показывает, что давление газа пропорционально среднему квадрату скорости, а не средней скорости.
1.7. Действительно, теплота есть не что иное, как движение молекул, но движение хаотическое, беспорядочное. Когда тело в целом покоится, его молекулы тем не менее могут обладать большой энергией хаотического движения. При этом мы говорим, что тело сильно нагрето (обладает высокой температурой). Если нагревать тело, т. е. дальше увеличивать его температуру, то скорость беспорядочного хаотического движения будет возрастать.
Молекулы холодного быстро движущегося бейсбольного мячика наряду с хаотической скоростью обладают еще скоростью направленного движения, одинаковой для всех молекул, которая характеризует энергию движения мячика как целого, а не его внутреннее состояние. Скорость же беспорядочного движения молекул холодного мячика меньше, чем нагретого.
1.8. Как бы ни были отполированы трущиеся поверхности машины, они никогда не будут совершенно гладкими. В действительности эти поверхности можно представить себе покрытыми (хотя и очень маленькими) бугорками, ступеньками и т. п. При движении таких поверхностей относительно друг Друга происходит множество микроскопических ударов, неровности сминают друг друга. В результате таких беспорядочных ударов в конце концов увеличивается скорость хаотического движения молекул (в § 2 «Лекций»,
вып. 1, показано, что при ударе молекулы о движущуюся ей навстречу поверхность, скорость молекулы увеличивается). А это означает, что трущиеся тела нагреваются.
1.9. Кусок резины состоит из длинных перекрывающихся цепочек атомов, которые беспорядочно ориентированы в пространстве. При растягивании резины, т. е. когда к ней приложена некоторая внешняя сила, часть этих цепочек вытягивается вдоль внешней силы. При этом «ориентирующиеся» цепочки атомов сталкиваются с другими молекулами резины и заставляют их двигаться быстрее, подобно тому, как вдвигаемый в сосуд с газом поршень заставляет двигаться быстрее молекулы газа. Поэтому температура куска резины
при его растяжении увеличивается, т. е. резина нагревается.
1.10. Резина с подвешенным на ней грузом растянута. Это значит, что некоторые молекулярные цепочки атомов расположены вдоль направления растяжения. В то же время все молекулы (цепочки) участвуют в беспорядочном тепловом движении и непрерывно сталкиваются друг с другом. В результате таких столкновений первоначально ориентированные цепочки атомов стремятся снова запутаться с остальными молекулами, но этому мешает приложенная внешняя сила. При нагревании резины скорость движения молекул увеличивается, усиливается бомбардировка ориентированных цепей, что приводит к более сильному их запутыванию. Последнее означает, что длина натянутой резины при нагревании уменьшается.
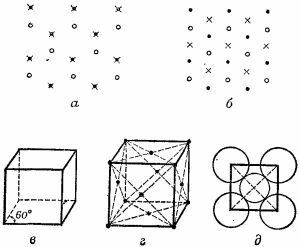 1.11. Посмотрим, как разместятся шарики при наиболее плотной упаковке (как раз тогда в сосуде поместится максимальное число шариков). Первый слой шариков ляжет так, что каждый шарик соприкоснется с шестью другими (положение центров шариков этого слоя показано на рис. а черными точками). Шарики второго слоя лягут в «ямки» первого слоя, так что каждый шарик второго слоя соприкоснется с тремя шариками нижнего (обратите внимание, что используется только половина «ямок» первого слоя), а в остальном второй слой выглядит точно так же, как первый, только смещен относительно него в вертикальном направлении. Центры шариков второго слоя, если смотреть на них сверху, займут положение, обозначенное на рис. а светлыми кружочками. Третий слой шариков можно наложить двумя разными способами: шарики могут лечь в те «ямки» второго слоя, которые находятся над центрами шариков нижнего слоя, тогда получится, что шарики третьего слоя лежат точно над шариками первого слоя (центры шаров верхнего слоя обозначены крестиками). Если же шарики третьего слоя лягут в другие «ямки» второго слоя, то окажется, что они будут находится как раз над «свободными ямками» первого слоя (рис. б). Плотность упаковки и в том и в другом случаях одинакова, т. е. число шариков в единице объема в обоих случаях одинаково. 1.11. Посмотрим, как разместятся шарики при наиболее плотной упаковке (как раз тогда в сосуде поместится максимальное число шариков). Первый слой шариков ляжет так, что каждый шарик соприкоснется с шестью другими (положение центров шариков этого слоя показано на рис. а черными точками). Шарики второго слоя лягут в «ямки» первого слоя, так что каждый шарик второго слоя соприкоснется с тремя шариками нижнего (обратите внимание, что используется только половина «ямок» первого слоя), а в остальном второй слой выглядит точно так же, как первый, только смещен относительно него в вертикальном направлении. Центры шариков второго слоя, если смотреть на них сверху, займут положение, обозначенное на рис. а светлыми кружочками. Третий слой шариков можно наложить двумя разными способами: шарики могут лечь в те «ямки» второго слоя, которые находятся над центрами шариков нижнего слоя, тогда получится, что шарики третьего слоя лежат точно над шариками первого слоя (центры шаров верхнего слоя обозначены крестиками). Если же шарики третьего слоя лягут в другие «ямки» второго слоя, то окажется, что они будут находится как раз над «свободными ямками» первого слоя (рис. б). Плотность упаковки и в том и в другом случаях одинакова, т. е. число шариков в единице объема в обоих случаях одинаково.
Укладывая таким же способом следующие слои шариков, замечаем, что их центры располагаются в пространстве в определенном порядке, т. е. образуют «кристаллическую» решетку. В первом из рассматриваемых случаев эта решетка , как легко заметить, имеет вид, приведенный на рис. в. Это так называемая гексагональная решетка.
Вид решетки, получающейся при втором способе укладки, приведен на рис. г (кубическая гранецентрированная решетка). Чтобы увидеть, что центры шариков расположены именно так, нужно представить себе, что одна из диагоналей куба, изображенного на рис. г, перпендикулярна горизонтальной плоскости, а шарики, центры которых лежат в вершинах куба, принадлежат четырем горизонтальным слоям.
Рассчитаем максимальное число помещающихся в сосуд шариков при каком-нибудь одном способе размещения, например втором. Длина ребра кубической гранецентрированной решетки, как видно из рис. д, равна l = √2d (d—диаметр шарика). С каждым таким кубом связано 14 шариков: 8 находятся в вершинах куба, а 6 лежат в середине каждой из его граней. Но внутри куба лежит только часть каждого
шарика, общий занимаемый ими объем равен объему 4 шариков (по половине от каждого из шариков, центры которых лежат на гранях куба и по 1/8 от шариков, находящихся в вершинах куба). В объеме V помещается всего V/V0 кубических ячеек, где V0=l3 = 2√2d3—объем одной ячейки, так что в сосуде объемом V может быть помещено самое большее N= 4V/V0 = √2V/d3 шариков.
 К главе 4. Сохранение энергии К главе 4. Сохранение энергии
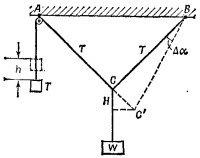
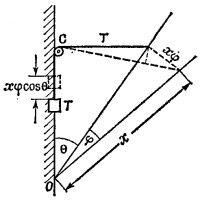
4.1. Представим себе, что груз весом W уравновешен при помощи некоторого другого грузика, который подвешен на маленьком блоке, как показано на рисунке. Вопрос о натяжении проволоки сводится, таким образом, к вопросу о величине веса грузика, так как натяжение проволоки равно весу грузика. Обозначим поэтому вес грузика через Т.
Предположим теперь, что грузик Т поднялся на небольшую высоту h. При этом груз W опустится на расстояние Н, а проволока ВС повернется на малый угол Δα.
Размеры проволок АС и АВ таковы, что угол АСВ прямой, поэтому Н =СС′ sin 45° = h/√2 (угол Δα—маленький, поэтому СС′ можно считать продолжением АС).
Увеличение потенциальной энергин грузика T по закону сохранения энергии равно уменьшению потенциальной энергии груза W, т. е. Th=WH, откуда
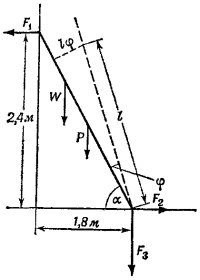 4.2. Введем следующие обозначения: F1— сила давления роликов на вертикальную стену; F2 и F3— горизонтальная и вертикальная составляющие силы давления лестницы на землю. Очевидно, что F1 направлена налево, F2— направо, а F3— вниз. Силы, приложенные к лестнице, равны по величине F1 F2 и F3 и направлены в противоположных направлениях. 4.2. Введем следующие обозначения: F1— сила давления роликов на вертикальную стену; F2 и F3— горизонтальная и вертикальная составляющие силы давления лестницы на землю. Очевидно, что F1 направлена налево, F2— направо, а F3— вниз. Силы, приложенные к лестнице, равны по величине F1 F2 и F3 и направлены в противоположных направлениях.
Рассмотрим следующие виртуальные перемещения лестницы. Пусть она сместится вниз параллельно себе самой на расстояние у. Неважно, что в действительности лестница так двигаться не может, ведь это перемещение воображаемое. В результате указанного перемещения потенциальная энергия лестницы и груза уменьшится на (W+P)y, а сила F3 совершит работу F3 у. Из закона сохранения энергии следует равенство этих двух величин, так что (W + P)y = F3y и, следовательно, F3=W+P = 36 кГ (Р — вес лестницы).
Выберем теперь другое виртуальное перемещение, состоящее в переносе лестницы параллельно себе в горизонтальном направлении, скажем вправо, на расстояние х. Аналогично предыдущему случаю можно написать F1x = F2x, откуда F1 = F2. Чтобы найти численные величины этих сил, необходимо иметь еще одно уравнение. Его можно получить, записав закон сохранения энергии при виртуальном повороте лестницы на небольшой угол вокруг оси, проходящей через нижний конец лестницы. Пусть α —угол, который образует лестница с Землей, а φ—тот малый угол, на который повернута лестница (по часовой стрелке). Точка, находящаяся на расстоянии / от оси вращения, опишет дугу длиной /φ. Так как угол φ мал, можно считать, что стягивающая дугу хорда имеет ту же длину и образует угол α, но с вертикальной стенкой (т. е. хорда перпендикулярна лестнице). Поэтому рассматриваемая точка при виртуальном повороте сместится вверх на величину /φcosα и вправо — на /φ sin α.
Используя только что полученный результат, убеждаемся в том, что при повороте на малый угол φ потенциальная энергия лестницы с грузом увеличится на 1/2PLφ cosα + 3/4WLφ cosα, а сила F1 совершит работу F1Lφ sin α (L — длина лестницы). Из закона сохранения энергии
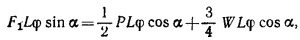 |
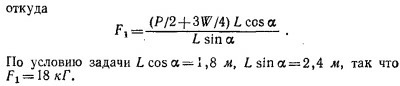 |
 4.3. Уравновесим стержень подъемного устройства грузом Т, подвешенным на малом блоке в точке С. При виртуальном повороте стержня по часовой стрелке на малый угол φ вокруг нижнего конца точка М стержня, находящаяся на расстоянии / от оси вращения, опустится вниз на расстояние lφ sin θ и сместится вправо на lφcos θ (см. предыдущую задачу). Поэтому при таком перемещении потенциальная энергия стержня и груза W уменьшится на (W + 1/2w) ·Lφ sin θ, а груз Т, как видно из рисунка, поднимется на высоту xφcos θ, т. е. его потенциальная энергия увеличится на Txφcos θ. Из закона сохранения энергии 4.3. Уравновесим стержень подъемного устройства грузом Т, подвешенным на малом блоке в точке С. При виртуальном повороте стержня по часовой стрелке на малый угол φ вокруг нижнего конца точка М стержня, находящаяся на расстоянии / от оси вращения, опустится вниз на расстояние lφ sin θ и сместится вправо на lφcos θ (см. предыдущую задачу). Поэтому при таком перемещении потенциальная энергия стержня и груза W уменьшится на (W + 1/2w) ·Lφ sin θ, а груз Т, как видно из рисунка, поднимется на высоту xφcos θ, т. е. его потенциальная энергия увеличится на Txφcos θ. Из закона сохранения энергии
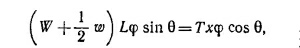 |
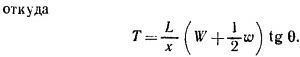 |
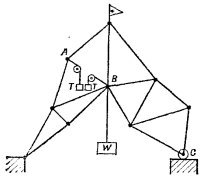 4.4. а) Представим себе, что стержень АВ фермы удален. Тогда под действием груза W шарнир В пойдет вниз направо, а шарнир А — вверх налево. Ясно поэтому, что стержень АВ был растянут. Однако и удалив стержень, мы тоже можем удержать ферму в равновесии, подвесив два равных груза на неподвижных блоках так, как это показано на рисунке. Если длина АВ увеличивается, грузы поднимаются и их потенциальная энергия возрастает. Чтобы потенциальная энергия всей системы оставалась неизменной, груз W должен опуститься. Следовательно, при нагревании стержня АВ груз W опускается, 4.4. а) Представим себе, что стержень АВ фермы удален. Тогда под действием груза W шарнир В пойдет вниз направо, а шарнир А — вверх налево. Ясно поэтому, что стержень АВ был растянут. Однако и удалив стержень, мы тоже можем удержать ферму в равновесии, подвесив два равных груза на неподвижных блоках так, как это показано на рисунке. Если длина АВ увеличивается, грузы поднимаются и их потенциальная энергия возрастает. Чтобы потенциальная энергия всей системы оставалась неизменной, груз W должен опуститься. Следовательно, при нагревании стержня АВ груз W опускается,
б) Вес рассматриваемых нами грузиков равен силе растяжения стержня Т (ферма находится в равновесии). Если увеличить длину АВ на величину х, грузы поднимутся вверх, причем сумма изменений высот грузов также равна х, а груз W опустится на у. Поэтому Tx = Wy, т. е. T = (y/x)W.
4.5. Пусть груз w опустится вниз на расстояние у. Потенциальная энергия груза при этом уменьшится на wy. Посмотрим, как изменится потенциальная энергия тележки весом W. Прежде всего заметим, что когда груз w опускается на расстояние у, ось подвижного блока, на котором он висит, опускается на вдвое меньшее расстояние. Так как тележка связана с грузом при помощи двух подвижных блоков, она передвинется по наклонной плоскости на расстояние в 4 раза меньшее, чем то, на которое опустится груз w, т. е. на величину у/4. По вертикали тележка поднимется на высоту у/4 sin θ, поэтому ее потенциальная энергия увеличится на 1/4Wysin θ. Из закона сохранения энергии 1/4Wysin θ = wy, откуда W=4w/sinθ.
4.6. Повернем катушку на угол φ против часовой стрелки вокруг ее оси. При этом груз W опустится на расстояние y = rφ, а центр тяжести катушки поднимется на х = rφ, т. е. груз W опустится на расстояние у—х. Из закона сохранения энергии W (у—x) = wx, откуда
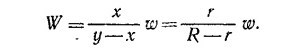 |
4.7. По условию задачи F1/F2 = R, где F1 и F2—силы, которые необходимо приложить к цепи для перемещения груза W вверх и вниз соответственно. Используем принцип виртуальной работы для этих двух случаев.
Предположим сначала, что, выбирая верхнюю часть ведущей цепи ворота с силой F1, мы повернули верхний блок на полный оборот против часовой стрелки. При этом мы, очевидно, протянули n звеньев цепи, или же n/N м, так как длина одного звена цепи равна 1/N м. Посмотрим теперь, что происходит с грузом W. Правая часть цепи, на которой висит подвижный блок, поднялась на n звеньев, зато левая опустилась на n — 1 звено, так что груз W поднялся на высоту [n—(n —1)]/2N м. Если обозначить через X работу сил трения при одном обороте верхнего блока, то из закона сохранения энергии имеем
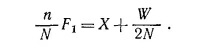 |
Чтобы повернуть верхний блок на один оборот по часовой стрелке, необходимо протянуть n—1 звено [или (n—1)/N м] нижней части ведущей цепи ворота с силой F2. При этом груз W опустится на расстояние [n—(n —1)]/2N м. Так как по предположению сила трения не зависит от направления движения груза W и поскольку каждый раз мы рассматриваем один полный оборот верхнего блока, работа сил трения в этом случае та же, что и в предыдущем, т. е. равна X. Согласно закону сохранения энергии,
Таким образом, для неизвестных сил F1 и F2 и работы сил трения получаем следующую систему трех уравнений:
Решая эту систему уравнений, находим
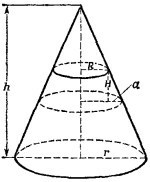 4.8. Выберем такое виртуальное перемещение цепи, при котором она опускается на расстояние Н вниз по вертикали параллельно самой себе. Потенциальная энергия ее при этом уменьшится на WH. Радиус же цепи при таком перемещении увеличится на величину а. Легко сообразить, что увеличение радиуса цепи и ее смещение вниз связаны соотношением a/H=r/h. Если натяжение цепи обозначить через Т, то виртуальная работа сил натяжения при рассматриваемом виртуальном перемещении цепи равна 4.8. Выберем такое виртуальное перемещение цепи, при котором она опускается на расстояние Н вниз по вертикали параллельно самой себе. Потенциальная энергия ее при этом уменьшится на WH. Радиус же цепи при таком перемещении увеличится на величину а. Легко сообразить, что увеличение радиуса цепи и ее смещение вниз связаны соотношением a/H=r/h. Если натяжение цепи обозначить через Т, то виртуальная работа сил натяжения при рассматриваемом виртуальном перемещении цепи равна
(R—радиус цепи). Но виртуальная работа силы Т равна изменению потенциальной энергии цепи, т. е. 2πаТ = WH.
Отсюда следует
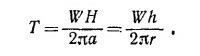 |
4.9. Повернем раму на небольшой угол φ. При таком повороте участок рамы AA′CD опустится вниз параллельно самому себе на расстояние AР·φ, а часть B′BGH таким же образом поднимется вверх на высоту РВ·φ. Так как противовес wc уравновешивает раму в отсутствие грузов, изменение его потенциальной энергии при любом изменении положения рамы равно по величине изменению потенциальной энергии самой рамы, поэтому в силу закона сохранения энергии должны быть равными и изменения потенциальной энергии грузов W1 и W2, т. е. W1AP·φ=W2BP·φ. Учитывая, что АР = 1/2ВР, находим W2 = 1/2W1 = 0,25 кГ.
4.10. Очевидно, вниз будет двигаться груз на той наклонной плоскости, которая образует больший угол с горизонталью. Легко убедиться в том, что, пройдя расстояние D вдоль наклонной плоскости, левый груз поднимется вверх на высоту D sin θ, а правый опустится вниз на расстояние D sin φ. Грузы при этом будут двигаться с некоторой скоростью v. Из закона сохранения энергии изменение потенциальной энергии грузов равно их кинетической энергии (вначале грузы покоились). Так как кинетическая энергия каждого груза равна Wv2/2g, а изменение потенциальной энергии грузов есть WD (sin φ—sin θ), то
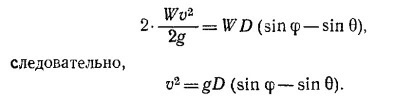 |
4.11. Так как углы наклона плоскостей одинаковы, грузы начнут двигаться так, что больший из них будет опускаться. При смещении на расстоянии D потенциальная энергия грузов уменьшится на (W1 — W2)D sin θ (см. предыдущую задачу), а их кинетическая энергия станет (W1+W2)v2/2g. Из закона сохранения энергии
4.12. Пусть уровень воды в баке уменьшится на небольшую глубину Δh. Это значит, что небольшая масса воды Δm = ρAΔh (Δh·A—объем вытекшей жидкости, а ρ—ее плотность) вытекла из сосуда через отверстие α с некоторой скоростью v. Так как площадь отверстия мала по сравнению с площадью поперечного сечения сосуда (α«А), скоростью изменения уровня жидкости в сосуде можно пренебречь. Изменение потенциальной энергии жидкости равно ΔmgH, а изменение ее кинетической энергии есть Δmv2/2. Из закона сохранения энергии
так что v=√2gH. Таким образом, в принятом приближении скорость вытекания жидкости не зависит ни от площади поперечного сечения сосуда, ни от сечения отверстия, а только от уровня жидкости над отверстием.
Можно учесть и скорость изменения уровня жидкости в сосуде, которую обозначим через v1 В этом случае изменение кинетической энергии равно
(а не Δmv2/2, как мы считали раньше). Через поперечное сечение сосуда в единицу времени протекает объем жидкости v1A, а через сечение α за то же время вытекает объем vα. Так как жидкость практически несжимаема, v1A = vα, так что v1 = (α/A)v.
Учитывая это, изменение кинетической энергии жидкости запишем как (Δm/2) v2[1 — (α/А)2], а закон сохранения энергии в виде (Δm/2) v2[1 — (α/А)2] = ΔmgH. Из последнего выражения находим скорость вытекания жидкости из сосуда:
4.13. I. Пусть стороны треугольника равны d1, d2 и L1, а угол между сторонами d1 и d2 равен α. Тогда, как известно, L2 = d12+ d22 — 2d1d2cosα. Увеличим угол α на небольшую величину Δα. Сторона, лежащая против этого угла, станет равной L1 т.е. увеличится на небольшую величину ΔL = L1— L. Но, по той же теореме косинусов, L12 = d12+ d22 — 2d1d2cos(α+Δα). Вспоминая, что cos(α+Δα) = cos α cos Δα — sin α sin Δα и что для малых углов cos Δα≈1, sin Δα ≈Δα, находим
Сравнивая эти выражения для разности квадратов сторон, получаем приведенную в тексте задачи формулу
II. Катеты а и b и гипотенуза с прямоугольного треугольника по теореме Пифагора связаны соотношением с2=а2+b2. Увеличим длины катетов на небольшие отрезки Δа и Δb, длина гипотенузы треугольника при этом также увеличится и станет равной с +Δc. Согласно теореме Пифагора, (с +Δc)2 = (а + Δа)2 + (b + Δb)2 или с2 + 2с Δс = а2 + 2аΔа + b2 + 2bΔb. Записывая последнее равенство, мы пренебрегли квадратами малых величин (Δа)2, (Δb)2 и (Δс)2 по сравнению с членами типа а2 и аΔа. Вычитая с2 из (c+Δс)2, находим
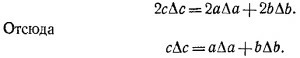 |
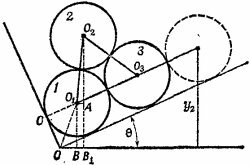 4.14. Пронумеруем бревна, как показано на рисунке. Пусть бревно 2 при небольшом уменьшении угла θ начнет двигаться вниз, выталкивая бревно 3 вверх по кузову. Ясно, что в конце движения бревно 2 займет положение бревна 3, а бревно 3—положение, показанное на рисунке пунктиром. Так как при первоначальном расположении бревна находились в равновесии, изменение потенциальной энергии бревен при рассмотренных перемещениях должно равняться нулю. Это возможно только в том случае, если центр бревна 2 в первом и центр бревна 3 во втором случаях находятся на одной и той же высоте. Обозначим указанные высоты через y1 и y2 соответственно. Вычисление у2 не вызывает никаких затруднений. Непосредственно из рисунка видно, что y2= R cos θ + 5R sin θ, где R — радиус бревна. 4.14. Пронумеруем бревна, как показано на рисунке. Пусть бревно 2 при небольшом уменьшении угла θ начнет двигаться вниз, выталкивая бревно 3 вверх по кузову. Ясно, что в конце движения бревно 2 займет положение бревна 3, а бревно 3—положение, показанное на рисунке пунктиром. Так как при первоначальном расположении бревна находились в равновесии, изменение потенциальной энергии бревен при рассмотренных перемещениях должно равняться нулю. Это возможно только в том случае, если центр бревна 2 в первом и центр бревна 3 во втором случаях находятся на одной и той же высоте. Обозначим указанные высоты через y1 и y2 соответственно. Вычисление у2 не вызывает никаких затруднений. Непосредственно из рисунка видно, что y2= R cos θ + 5R sin θ, где R — радиус бревна.
Для вычисления у1 замечаем, что y1= О2А +О1В. Из прямоугольного треугольника О1О2А находим
так как O1O2O3 равносторонний треугольник со стороной 2R, a < O3O1A=θ. Из треугольника ОО1В следует
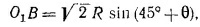 |
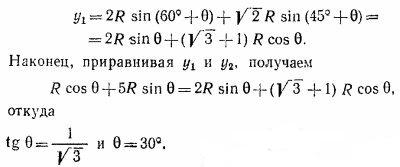 |
4.15. а) Гибкими связями можно заменить те стержни, которые растянуты. Чтобы выяснить, сжат данный стержень или растянут, удобно воспользоваться следующим простым приемом. Представим, например, что стержень АВ фермы удален. Тогда груз W пойдет вниз, а точка В начнет перемещаться к точке А. Стержень АВ препятствует такому движению, следовательно, он сжат. Удалим стержень АС. Груз W снова начнет двигаться вниз, а шарниры А и С разъедутся. Стало быть, стержень АС растянут. Удаляя последовательно каждый стержень фермы, можно убедиться, что стержни ВС, АС, СЕ, EG, ED и EF растянуты, т. е. их можно заменить гибкими связями. Все остальные стержни сжаты.
б) Удалим стержень BD. Чтобы ферма осталась в равновесии, к ней нужно на двух блоках подвесить два груза по ТBD каждый, как показано на рисунке (TBD — усилив в стержне BD). Рассмотрим следующее виртуальное перемещение. Представим себе, что ферма переломилась в шарнире С, в результате чего часть фермы GFDCE повернулась как целое на небольшой угол ΔΨ вокруг шарнира G, а часть ABC —на угол ΔΨ вокруг шарнира А. Углы Δφ и ΔΨ считаем малыми, такими, чтобы смещением точки А можно было пренебречь.
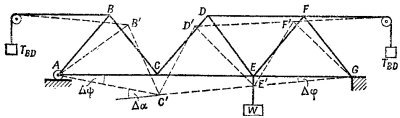 |
При таком перемещении фермы груз W опустится вниз на расстояние ЕЕ′ =EG·Δφ, а подвешенные на блоках грузики поднимутся вверх. Как видно из рисунка, сумма высот подъема грузов равна BD — B′D′ = ΔBD. Чтобы найти эту величину, удобно воспользоваться формулой, доказанной в пункте (I) задачи 4.13; для этого нужно лишь определить изменение угла BCD: Δα = <BCD — <В′С′D′ . Легко убедиться в том, что Δα = Δφ+ ΔΨ. Но СС′=СGΔφ = AСΔΨ, так что ΔΨ = (CG/AC) Δφ = 2Δφ, поэтому Δα = ЗΔφ.
Таким образом,
так как sin <BCD = 24/25. (Все стороны треугольника BCD известны, поэтому вычисление синуса не представляет труда.)
Из закона сохранения энергии TBDΔBD = WEGΔφ, откуда
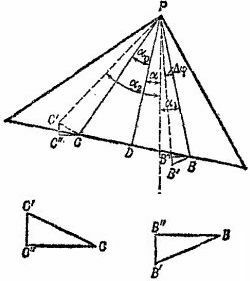 4.16. Если стержень находится в равновесии, то, повернув его на малый угол Δφ около точки Р, мы должны обнаружить, что потенциальная энергия не изменилась. Зто означает, что потенциальная энергия одного из кусков увеличивается, а другого уменьшается, в точности компенсируя это увеличение. Так как потенциальная энергия однородного стержня зависит от высоты его середины, нужно определить, как изменятся высоты середин кусков при повороте на угол Δφ (см. рисунок). Как видно из рисунка (для удобства треугольники ВВ′В″ и СС′С″ нарисованы отдельно), середина куска весом 2W опустится на величину B′B″=sin α1·BB′ а середина куска весом W поднимется на С′С″ = sin α2·CC′, Итак, 4.16. Если стержень находится в равновесии, то, повернув его на малый угол Δφ около точки Р, мы должны обнаружить, что потенциальная энергия не изменилась. Зто означает, что потенциальная энергия одного из кусков увеличивается, а другого уменьшается, в точности компенсируя это увеличение. Так как потенциальная энергия однородного стержня зависит от высоты его середины, нужно определить, как изменятся высоты середин кусков при повороте на угол Δφ (см. рисунок). Как видно из рисунка (для удобства треугольники ВВ′В″ и СС′С″ нарисованы отдельно), середина куска весом 2W опустится на величину B′B″=sin α1·BB′ а середина куска весом W поднимется на С′С″ = sin α2·CC′, Итак,
Заметим далее, что α1=α0— α а α2 = α0+ α (α—искомый угол). Пользуясь формулами для синуса суммы и разности углов, находим
получаем окончательно
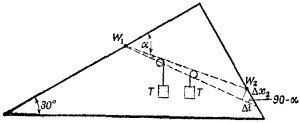 4.17. Грузы W1 и W2 на проволочной рамке можно уравновесить, подвесив на двух блоках два других груза весом Т каждый (Т — натяжение нити), как показано на рисунке. Пусть груз W2 сдвинется на небольшое расстояние Δx2 вниз по проволоке, а груз W1 останется неподвижным. При таком перемещении груз W2 опустится по вертикали на расстояние Δx2 cos 30°, а грузы Т поднимутся вверх на величину Δ/ = Δx2 cos (90s—α) (Δ/ — удлинение нити при выбранном виртуальном перемещении). Согласно закону сохранения энергии 4.17. Грузы W1 и W2 на проволочной рамке можно уравновесить, подвесив на двух блоках два других груза весом Т каждый (Т — натяжение нити), как показано на рисунке. Пусть груз W2 сдвинется на небольшое расстояние Δx2 вниз по проволоке, а груз W1 останется неподвижным. При таком перемещении груз W2 опустится по вертикали на расстояние Δx2 cos 30°, а грузы Т поднимутся вверх на величину Δ/ = Δx2 cos (90s—α) (Δ/ — удлинение нити при выбранном виртуальном перемещении). Согласно закону сохранения энергии
Сместим теперь вниз по проволоке на расстояние Δх1 груз весом W1, а второй оставим неподвижным. Те же рассуждения приведут нас к уравнению
Решая полученные два уравнения для α и T, легко найти
К главе 6. Вероятность
6.1. Как было показано в § 3 гл. 6 «Лекций» (вып. 1), при случайных блужданиях молекула, сделав N шагов, отклонится от первоначального положения в среднем на расстояние D = √ NI, где I—длина одного шага (в нашем случае это просто длина свободного пробега молекулы между двумя последовательными столкновениями). Заметим, что используемая нами формула для пройденного расстояния (среднего квадратичного отклонения) отличается от формулы (6.10) «Лекций» (вып. 1, стр. 112) тем, что в ней явно фигурирует длина одного шага (в «Лекциях» же длина шага принята равной единице и поэтому явно в формулу не входит).
Итак, чтобы удалиться на расстояние D, молекула должна сделать N=D2/l2 шагов. Каждый шаг совершается за промежуток времени т = l/ (—средняя скорость молекулы), т. е. за время между двумя последовательными столкновениями молекулы. Поэтому для преодоления расстояния в 1 см молекуле понадобится время
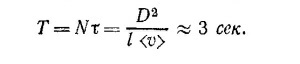 |
6.2.Число существенно различных способов вынуть 3 шарика из 6 равно С36 = 20. Из всех этих способов только одним способом можно вынуть все три шарика одного цвета (нужно, чтобы все шарики были красными) и, как легко подсчитать, шестью —разного цвета (три возможности—белый шарик, первый зеленый шарик, один из трех красных; другие три способа—белый шарик, второй зеленый шарик и один из трех красных шариков). Поэтому вероятность того, что все шарики окажутся одного цвета, равна 1/20; вероятность же того, что все три шарика окажутся разного цвета, равна 6/20 = 3/10.
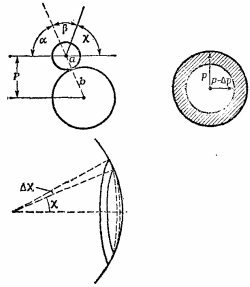 6.3.Обозначим через р расстояние от центра шарика до оси, проходящей через центр неподвижной сферы параллельно скорости шарика (так называемый прицельный параметр). Как видно из рисунка, p = (a + b)sinα, где α—угол между скоростью шарика и радиусом сферы, проведенным в точку попадания шарика, т. е. угол падения. Введем угол рассеяния x — угол между начальной и конечной скоростями 6.3.Обозначим через р расстояние от центра шарика до оси, проходящей через центр неподвижной сферы параллельно скорости шарика (так называемый прицельный параметр). Как видно из рисунка, p = (a + b)sinα, где α—угол между скоростью шарика и радиусом сферы, проведенным в точку попадания шарика, т. е. угол падения. Введем угол рассеяния x — угол между начальной и конечной скоростями
шарика. Учитывая, что угол падения равен углу отражения, находим x = π—2α.
Итак, угол рассеяния целиком определяется углом падения, т. е. в конечном итоге прицельным расстоянием. Если посмотреть со стороны движущихся шариков, то точки попадания шариков с одним и тем же прицельным расстоянием р образуют окружность радиусом р. Шарики с несколько меньшим прицельным расстоянием р — Δр отклоняются на больший угол x+Δx. Очевидно, что все шарики, попавшие на заштрихованное кольцо, отклоняются на углы, лежащие между x и x+Δx. Если Δр мало, то площадь этого кольца,равна 2πрΔр, а число шариков, попадающих на него в единицу времени, равно n·2πрΔр, где n — плотность потока, т. е. число шариков, проходящих в единицу времени через единичную площадку, расположенную нормально к потоку. Выразим теперь Δр через x и Δx. Так как α = (π—x)/2, то
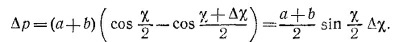 |
[Мы учли здесь то обстоятельство, что при малых Δх sin Δх/2≈Δх/2 и sin ((х + Δх)/2) ≈ sin x/2.] Таким образом, число частиц, рассеянных в единицу времени на углы от х до x+Δx, равно
Если сечение потока шариков равно S, то доля шариков, рассеянных на углы от x до x+Δx, равна
Величину Δσ называют сечением рассеяния. Имеем
Эту формулу полезно записать в несколько ином виде. Представим себе сферу единичного радиуса и отложим из центра этой сферы векторы, изображающие скорости рассеянных шариков. Тогда векторы, отвечающие шарикам, рассеянным в интервале углов от x до x+Δx, «пронижут» нашу сферу по кольцу, показанному на рисунке. Средний радиус этого кольца приблизительно равен sin x, а площадь (для малых Δx) 2π sin xΔx. Обозначив эту площадь через ΔΩ, запишем
Наш результат можно выразить словами: сечение рассеяния в направления, лежащие в некотором телесном угле, пропорционально величине этого угла. Заметим, что полное сечение рассеяния σ на все углы (Ω = 4π) равно π(a+b)2, что, конечно, вполне естественно.
К главе 7. Теория тяготения
7.1. Элементы орбиты Луны приведены в условии задачи. Для спутника же расстояния от центра Земли в перигее и апогее равны соответственно
Для определения периода спутника Тс воспользуемся третьим законом Кеплера Тc2/ТЛ2 = ac3/aл3, где ас и ал — большие полуоси орбит спутника и Луны соответственно, а Tл —период обращения Луны.
Выразим длину большой полуоси орбиты через rр и rа, воспользовавшись для этого формулами, приведенными на стр. 19:
Подставляя а в формулу для отношения периодов, находим
 В нашем случае это дает Tс=1,55 час. В нашем случае это дает Tс=1,55 час.
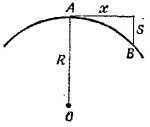
7.2. а) Так как спутник движется по круговой орбите радиусом R, то, сместившись на х в горизонтальном направлении, он одновременно переместится на расстояние s по вертикали. Выпишем формулу, связывающую s и х (см. «Лекции», вып. 1, подпись к рис. 74, стр. 127):
(s считаем малым, т. е. считаем, что прошло, очень мало времени с того момента, как спутник побывал в точке А). Таким образом,
Длина дуги АВ равна vt (v — скорость спутника). Но если эта длина мала, то можно считать, что и х ≈ vt, следовательно,
С другой стороны, формула пути для равноускоренного движения имеет вид s = at2/2. Сравнивая эти две формулы, видим, что центростремительное ускорение спутника aц = v2/R.
б) Если положить a = GM/R2, то
Период обращения есть время, за которое тело совершает один оборот, так что T=2πR/v, или
Найденное выражение для Т соответствует третьему закону Кеплера: квадрат периода пропорционален кубу большой полуоси орбиты (в нашем случае круговой орбиты—ее радиусу) (см. § 2 гл. 7 «Лекций», вып. 1, стр. 123).
7.3. а) Будем считать, что Луна вращается вокруг Земли по круговой орбите радиусом Rл=380 000 км с периодом Тл = 27,3 дня, а Земля вращается вокруг Солнца по такой же орбите с параметрами R3 = 149 500 000 км; Т3 =365,25 дня.
Воспользуемся формулой для периода обращения спутника, полученной в предыдущей задаче:
Записав периоды обращения Луны и Земли и взяв их отношение, получим
где МC и М3 — масса Солнца и Земли соответственно, откуда
б) Рассмотрев аналогично движение Луны вокруг Земли и спутника Ио вокруг Юпитера, получим
где МЮ—масса Юпитера, а ТИо и RИо—период обращения и радиус орбиты спутника Ио.
7.4. Пусть массы М1 и М2 вращаются по круговым орбитам с радиусами r1 и r2 соответственно, причем r1+r2 = R (R — постоянное расстояние между массами). Вращаясь вокруг неподвижной точки (их общего центра масс), эти тела все время находятся на одной прямой, соединяющей данные массы и проходящей через неподвижную точку вращения. Поэтому периоды обращения обоих тел одинаковы и равны Т.
Рассмотрим движение одного тела, например первого. Сила притяжения, действующая на него со стороны второго тела, равна
Как было показано в задаче 7.2, под действием этой силы тело движется с центростремительным ускорением
Учитывая, что период обращения T = 2πr1/v1 и что F(1) =M1aц(1) (см. § 3 гл. 7 «Лекций», вып. 1), получаем
Аналогично можем написать для второго тела:
Складывая два последних выражения и учитывая, что r1+r2 = R, находим
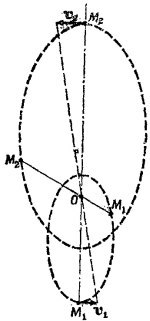 Полученная формула показывает, что период обращения тел зависит только от расстояния между ними и их суммарной массы (а не массы каждого из тел или же отношения их масс). Полученная формула показывает, что период обращения тел зависит только от расстояния между ними и их суммарной массы (а не массы каждого из тел или же отношения их масс).
Перейдем теперь к случаю эллиптических орбит. Речь идет в сущности о трех эллипсах: по эллипсам движутся оба тела (легкое—по большому, тяжелое—по малому) и, кроме того, относительное движение тел также происходит по эллипсу (см. «Лекции», вып. 1, гл. 7). Все три эллипса подобны друг другу, т. е. обладают одним и тем же эксцентриситетом. Если учесть также, что центр масс системы остается неподвижным (он лежит в общем фокусе орбит обоих тел), а расстояния от центра масс до тел обратно пропорциональны их массам, то мы придем к выводу, что расположение тел и их орбит такое, как на рисунке.
Обозначив через v1 и v2 скорости тел М1 и M2 в тот момент времени, когда они находятся в апогее. Как видно из рисунка,
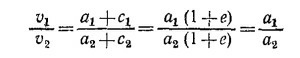 |
(индексами 1 и 2 обозначены величины, относящиеся к эллипсам, по которым движутся массы М1 и М2).
Чтобы получить для эллиптических орбит те же выражения, что и для круговых, вспомним, что эллипс можно представить себе как окружность, видимую под некоторым углом к своей плоскости или (что то же самое) как проекцию окружности на наклонную плоскость. Иначе говоря, эллипс можно получить из окружности, если изменить масштаб вдоль одной из осей координат. Ускорение тела при движении его по окружности было вычислено в «Лекциях» (вып. 1, гл. 7, подпись к рис. 7.4, стр. 127). Чтобы получить ускорение тела (например, М1) в интересующем нас случае, представим себе, что его орбита получена из круговой увеличением масштаба в «вертикальном направлении» в a1/b1 раз. Величина х при этом не изменится, а s увеличится и станет равным s1 = (a1/b1)s.
Подставив в соотношение x2 = 2Rs (справедливое для окружности) их значения после увеличения масштаба х1 = х, s1 = (a1/b1)s и R=b1 («горизонтальные» размеры не изменились, поэтому малая полуось эллипса равна радиусу исходной окружности), получим
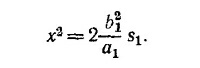 |
Таким образом, радиус кривизны эллипса в точке пересечения с большой полуосью равен b12/a1. Считая, что в течение очень малого промежутка времени первое тело движется по круговой орбите этого радиуса, можно написать
(здесь а и с — параметры орбиты относительного движения тел: a = a1+a2, c = c1+c2). Аналогично для второго тела
Складывая последние два равенства и выражая v2 через v1 получаем
Остается лишь выяснить, какое отношение имеет к периоду обращения величина, стоящая в левой части этого равенства. Заметим прежде всего, что площадь, которую за единицу времени «заметает» радиус-вектор тела M1 (проведенный из точки 0), равна 1/2v1 (a1 + c1) = 1/2v1a1 (1+е). Хотя фактически мы вычислили скорость изменения «заметаемой» площади для того момента, когда тело М1 находится в апогее, согласно второму закону Кеплера, эта скорость не меняется при движении тела по орбите. Поэтому величина 1/2v1a1 (1+е)Т (здесь Т—период обращения) равна площади орбиты тела М1. Площадь эллипса легко вычислить, если сообразить, что при увеличении масштаба по одной из осей площадь фигуры увеличивается во столько же раз, что и масштаб. Поэтому площадь эллипса равна
7.5. Как было показано в предыдущей задаче, квадрат периода обращения двух тел вокруг их центра масс есть
(Здесь R — большая полуось относительного движения двух звезд.)
Применяя эту формулу к движению двух звезд а и b и к системе Солнце — Земля, пишем
R3 и Т3 —большая полуось земной орбиты и период обращения Земли.) Беря отношение этих периодов и пренебрегая массой Земли по сравнению с массой Солнца, получаем
T3=1 год; RЗ =1A.E. (по определению астрономической единицы длины), так что
7.6. а) Предположим, что плоскость орбиты системы Сириуса перпендикулярна направлению на Землю. В этом случае по рис. 7.7 «Лекций» (вып. 1, стр. 131) можно определить величину большой полуоси орбиты Сириуса В (в угловых единицах). Она оказывается равной примерно 7,30″. Из того же рисунка можно заключить, что период обращения системы около 45 лет.
В предыдущей задаче было показано, что при орбитальном движении различных тел можно установить соотношение
(обозначения те же, что и в задаче 7.5).
Отсюда суммарная масса двойной звезды Сириуса равна
б) Это значение массы есть ее нижний предел, так как если плоскость орбиты не перпендикулярна направлению на Землю, то ее большая полуось в действительности больше ее видимого с Земли размера. Масса двойной звезды пропорциональна кубу большой полуоси, так что минимальной величине полуоси соответствует минимальное же значение массы.
7.7. Орбитальная скорость планеты такова, что за равные промежутки времени т ее радиус-вектор «заметает» равные площади (второй закон Кеплера). Рассмотрим движение Земли вблизи перигея и апогея за такие малые интервалы времени Δt, чтобы ее траекторию можно было считать прямолинейной. Тогда «заметаемые» площади есть треугольники с основаниями vминΔt и vмаксΔt и высотами rа и rр соответственно, так что
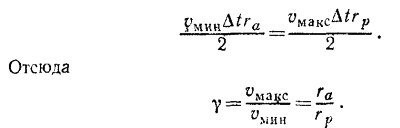 |
Но для эллипса ra = a(1+e), a rp = a(1—е); следовательно, γ = (1+е)/(1—е) ≈1+2е (поскольку е«1). Это дает γ≈ 1,0334.
7.8. а) По данным о появлении кометы находим ее период Т обращения вокруг Солнца. Он равен Т = 76 лет. Пользуясь третьим законом Кеплера, найдем большую полуось а орбиты кометы
где а3 и Т3 —большая полуось орбиты и период обращения Земли.
Если измерять а в А.Е., а T в годах, то
б) В предыдущей задаче было показано, что отношение максимальной и минимальной скоростей γ равно отношению расстояний в апогее и перигее. Итак,
7.9. В задаче 7.4 было показано, что период обращения двух тел вокруг их общего центра масс равен
где R — расстояние между телами; М1 и М2 — их массы, а G — постоянная в законе тяготения.
Применив эту формулу к системе Земля—Луна, найдем массу Луны:
(ТЛ—период обращения Луны вокруг Земли, М3 —масса Земли, МЛ—масса Луны, Rл — расстояние от Земли до Луны).
Достижения современной ракетной техники дают нам еще один способ определения массы Луны. Запустив искусственный спутник Луны и определив его период обращения Т и большую полуось его орбиты R, записываем (см. задачу 7.2)
(мы пренебрегли массой искусственного спутника по сравнению с массой Луны).
Или, чтобы исключить G (см. задачу 7.3):
7.10. Тело массы m, находящееся на поверхности Земли, притягивается к ней с силой
Но F = mg3, где g3—ускорение силы тяжести на Земле. Приравнивая эти два выражения, получаем
(MЛ gЛ RЛ — масса, радиус и ускорение силы тяжести Луны). Сравнивая gЛ и g3, находим
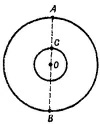 7.11. Пусть лаборатория, где производится эксперимент, расположена в точке С Земли. На тела, находящиеся в лаборатории, действуют силы притяжения Земли и Луны, причем эти силы вычитаются, если Луна находится в точке А, или складываются, если Луна находится в точке В. Ускорение свободного падения для этих двух случаев равно 7.11. Пусть лаборатория, где производится эксперимент, расположена в точке С Земли. На тела, находящиеся в лаборатории, действуют силы притяжения Земли и Луны, причем эти силы вычитаются, если Луна находится в точке А, или складываются, если Луна находится в точке В. Ускорение свободного падения для этих двух случаев равно
где R — расстояние от центра Земли до Луны.
Очевидно, что g1 и g2—минимальное и максимальное значения, которые ускорение g принимает в течение суток.
Таким образом, самое большое изменение ускорения свободного падения тел за счет суточного вращения Земли равно
(мы учли, что RЗ «R).
Среднее ускорение силы тяжести равно GMЗ/RЗ2.
Таким образом,
Следовательно, величину g нужно измерять с точностью не меньшей, чем до пятого знака, чтобы уловить ее изменение вследствие суточного вращения Земли.
К главе 8. Движение
8.1. Известно [формула (8.9) «Лекций», вып. 1, стр. 153], что ускорение есть производная скорости по времени: а = dv/dt.
Стало быть, нужно подобрать такую функцию vx(t), чтобы ее производная была постоянной и равной а. Легко убедиться в том, что vx(t) = at+c, где с—некоторая постоянная величина (ее производная равна нулю!). Физический смысл постоянной с легко выяснить, если положить t = 0 в формуле для vx(t). Тогда c = vx(0) = vx0.
Вспомним теперь, что v = dx/dt и подберем x(t) так, чтобы получилась нужная производная.
Очевидно, x(t)= at2/2+vx0t+d. Снова, полагая t = 0, убеждаемся, что здесь d = x (0) = х0.
8.2. Из полученного в предыдущей задаче выражения для скорости находим t = (vx—vX0)/a. Подставляя это выражение
в формулу для х, получаем
8.3. Для движений вдоль осей х, у, z можно непосредственно написать
Последнее выражение задачи 8.2 можно записать как
Обобщая его на случай движения вдоль осей у и z, имеем
Складывая три последних равенства и учитывая формулу (8.16) «Лекций» (вып. 1, стр. 155), получаем
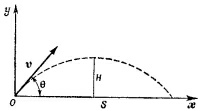 8.4. Обозначим расстояние, которое пролетит снаряд по горизонтали, через S, а максимальную высоту его полета —через H. В начальный момент времени (t = 0), х0=0, у0 = 0, а vx0 = v cos θ, vy0 = v sin θ (см. § 5 гл. 8 «Лекций», вып, 1, стр. 152). Используя результаты задачи 8.3, находим 8.4. Обозначим расстояние, которое пролетит снаряд по горизонтали, через S, а максимальную высоту его полета —через H. В начальный момент времени (t = 0), х0=0, у0 = 0, а vx0 = v cos θ, vy0 = v sin θ (см. § 5 гл. 8 «Лекций», вып, 1, стр. 152). Используя результаты задачи 8.3, находим
(здесь учтено, что ау = – g).
Очевидно, расстоянию S по оси х соответствует y = 0; отсюда можно найти момент падения снаряда на землю:
Решению t1 = 0 соответствует просто начальное положение х = 0, y = 0. Значит,
Из соображений симметрии понятно, что максимальная высота достигается снарядом в момент времени t′ = t2/2, откуда
8.5. В предыдущей задаче было показано, что дальность горизонтального полета снаряда определяется формулой
Максимальной дальности полета соответствует такой угол вылета θ, что sin 2θ = 1. Отсюда θ = π/4.
8.6. Запишем выражение для пройденного пути при ускоренном движении автомобиля: s (t) = v0t + 1/2аt2, где v0—скорость
автомобиля в начале ускоренного движения, а — его ускорение.
Учитывая, что в момент времени t1= 16 сек путь s1 = 0,1 мили, а при t2= 16 + 8 = 24 сек s2 = 0,2 мили, записываем два уравнения для а и v0:
Используя эти значения а и v0, находим скорость автомобиля в момент времени t2:
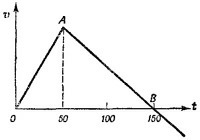 8.7. а) В промежуток времени от t0 = 0 до t1 = 50 сек, т. е. во время работы двигателя, ракета двигалась с ускорением 2g. Значит, в этом интервале времени скорость ракеты определяется формулой 8.7. а) В промежуток времени от t0 = 0 до t1 = 50 сек, т. е. во время работы двигателя, ракета двигалась с ускорением 2g. Значит, в этом интервале времени скорость ракеты определяется формулой
Графиком этой зависимости является прямая (отрезок OА). С момента времени t = 50 сек и дальше до падения на Землю ракета движется с ускорением –g, так что
График этой функции тоже прямая (справа от точки А).
б) Так как вертикальная скорость обращается в нуль в наивысшей точке траектории, моменту времени tB соответствует максимальная высота полета ракеты. Таким образом,
в) С высоты Hмакс (с момента времени tB) ракета свободно Падает вниз. Землю она достигает через t′ сек, причем
8.8. Обозначим ускорение тележки с ракетным двигателем через а1 а с авиационным—через а2. Пусть 2S —проходимый тележками путь. Тележка с ракетным двигателем первую половину пути проходит за время t1 определяемое из уравнения
где v0—скорость тележки в конце первой половины пути, т. е. v0 = a1t1, откуда
Тележка с реактивным двигателем проходит все расстояние за время t, такое, что
8.9. Угол, под которым должна быть выпущена мина, чтобы пройти возле края обрыва, определим по формуле (см. задачу 8.4.)
Зная, что S = 8100 м, v0 = 300 м/сек, получаем sin2α = 0,882 и α1=31°, α2=59°.
Очевидно, чем больше будет угол, под которым выпущена мина, тем ближе она упадет к основанию обрыва, поэтому в нашем случае следует выбрать больший из углов, т. е. α2.
Рассмотрим теперь движение мины за краем обрыва. Скорость мины вблизи края обрыва направлена под углом α=59° к горизонту. Следовательно, до падения на землю мина пролетит по горизонтали расстояние Sмин = v0t cos α (t — время движения за краем обрыва). Вычислим t. Так как вертикально вниз мина движется с начальной скоростью v0 sin α и ускорением g, то h= v0t sin α +gt2/2 (h —высота обрыва). Подставляя вместо h, v0 и α их численные значения, находим t = 0,408 сек, SминI ≈63 м.
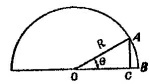 8.10. а) Известно, что θ = S/R. По определению sin θ = AC/R, а cos θ = OC/R. При малых углах θ дугу АВ можно заменить перпендикуляром АС, а ОС — радиусом R. В этом случае sin θ ≈ S/R = θ и cos θ ≈ R/R = 1 8.10. а) Известно, что θ = S/R. По определению sin θ = AC/R, а cos θ = OC/R. При малых углах θ дугу АВ можно заменить перпендикуляром АС, а ОС — радиусом R. В этом случае sin θ ≈ S/R = θ и cos θ ≈ R/R = 1
б) Вычисление производных sin x и cos x ясно из приведенных ниже формул:
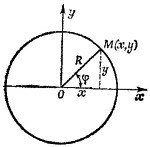 8.11. а) Пусть тело в момент времени t окажется в точке М (х, у) окружности. Обозначим через φ угол между радиусом этой точки и положительным направлением оси х. Как видно из рисунка, координаты этой точки: 8.11. а) Пусть тело в момент времени t окажется в точке М (х, у) окружности. Обозначим через φ угол между радиусом этой точки и положительным направлением оси х. Как видно из рисунка, координаты этой точки:
Производную dφ/dt (скорость изменения угла со временем) назовем угловой скоростью ω.
Таким образом, v = ωR, или ω = v/R. Поскольку v не зависит от времени, то и ω не зависит от времени, так что φ = ωt. Вообще говоря, следовало бы написать φ = ωt +c, но по условию задачи φ = 0 при t = 0, так что c = 0. Следовательно, х= R cos ωt, y=R sin ωt,
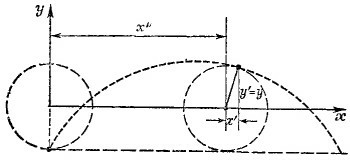 8.12. Координату х камешка удобно представить в виде суммы х = х′ +х″, где х′—координата относительно оси колеса, а х″—координата оси колеса (см. рисунок). Выражение для х′ и у′ получены в предыдущей задаче (мы должны лишь заменить в соответствующих формулах ωt на —ωt, так как, когда колесо катится в положительном направлении оси х, оно вращается по часовой стрелке, а в предыдущей задаче рассмотрено вращение против часовой стрелки). Итак, 8.12. Координату х камешка удобно представить в виде суммы х = х′ +х″, где х′—координата относительно оси колеса, а х″—координата оси колеса (см. рисунок). Выражение для х′ и у′ получены в предыдущей задаче (мы должны лишь заменить в соответствующих формулах ωt на —ωt, так как, когда колесо катится в положительном направлении оси х, оно вращается по часовой стрелке, а в предыдущей задаче рассмотрено вращение против часовой стрелки). Итак,
Если исключить из этих соотношений время, то мы получим зависимость у(х), которая графически изображается кривой, называемой циклоидой (см. рисунок). Дифференцируя полученные выше выражения для х и у по времени, получаем
К главе 9. Динамические законы Ньютона
9.1. Поскольку сила перпендикулярна скорости, то она не может изменить модуль скорости, а может лишь изменить ее направление. Так как модуль скорости постоянен, то постоянна и сама сила (F = βv). Эта сила вызывает ускорение (в направлении, перпендикулярном к v), величина которого определяется из соотношения ma = βv, т. е. a=βv/m.
В § 4 гл. 7 «Лекций» (вып. 1) рассматривалось такого рода движение с постоянной по величине скоростью и постоянным ускорением, перпендикулярным скорости. Было показано (см. задачу 7.2), что это есть движение по окружности с радиусом R=v2/a = mv/β.
9.2. При вычислении радиусов кривизны воспользуемся формулой для ускорения, перпендикулярного скорости
Таким образом, в дополнение к величинам, приведенным в табл. 9.2 «Лекций» (вып. 1, стр. 170), следует вычислить также величины dv/dt и v2. Проведя вычисления, находим для радиуса кривизны орбиты:
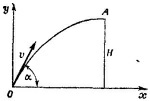 9.3. а) Мяч влетел в окно горизонтально; это означает, что окно находилось в наивысшей точке траектории мяча. Максимальная же высота подъема определяется по формуле (см. задачу 8.4) 9.3. а) Мяч влетел в окно горизонтально; это означает, что окно находилось в наивысшей точке траектории мяча. Максимальная же высота подъема определяется по формуле (см. задачу 8.4)
б) В наивысшей точке скорость горизонтальна, а ускорение равно —g (ускорение свободного падения), вертикально и, таким образом, перпендикулярно скорости. Поэтому
Определим теперь радиус кривизны в произвольный момент времени t.
Обозначив через а– и a|| компоненты ускорения — перпендикулярную и параллельную скорости, запишем
9.4. Все величины в системе M′K′S′A′ будем обозначать буквой со штрихом. Без штриха будем обозначать те же величины в системе MKSA. Очевидно,
9.5. В системе единиц M′K′S′A′ сила тяготения запишется в виде
(При получении этой формулы был использован результат предыдущей задачи: F′ =(μλ/τ2) F.)
9.6. Заметим прежде всего, что величина GMO в штрихованной системе единиц и в системе MKS связаны между собой соотношением
За единицу длины в рассматриваемой системе единиц берется длина большой полуоси орбиты Земли, т. е. расстояние в 14,9·1010 м. Поэтому длина l′ в А.Е. через длину / выражается так:
Величину G′M′O можно легко вычислить и другим способом, если вспомнить выражение для периода обращения планеты, полученное нами в задаче 7.4:
Применяя эту формулу для системы Солнце—Земля и пренебрегая массой Земли по сравнению с массой Солнца, получаем
9.7. В модели Солнечной системы все расстояния измеряются числами, в k раз меньшими, чем в «натуральной» системе. Представим себе, что это изменение чисел произошло не вследствие реального уменьшения размеров системы, а в результате перехода к новой системе единиц, такой, что l′ =kl. Но тогда и все единицы, размерность которых включает длину, так же претерпят определенные изменения. В частности, плотность ρ = т/l3 станет равной
По условию задачи ρ′ = ρ. Это значит, что нужно взять новую единицу измерения не только для длины, но и для массы тела, причем, очевидно, m′ = k3m.
Как было показано в задаче 7.4, период обращения Т планеты вокруг Солнца выражается через суммарную массу М Солнца и планеты и большую полуось орбиты R, так что
Здесь мы использовали доказанное в предыдущей задаче соотношение
(Роль λ задачи 9.6 у нас играет k, а т=1.) Таким образом, мы убеждаемся, что периоды обращения «планет» в изготовленной модели будут такими же, как и в реальной Солнечной системе.
9.8. Изменение потенциальной энергии при движении грузов равно изменению потенциальной энергии маленького разновеска (насколько одна масса М опустится, настолько другая поднимется), т. е. Δи = mgh. Если тела в начальный момент покоились, то это изменение потенциальной энергии равно кинетической энергии всей системы в тот момент, когда подхватывается разновесок:
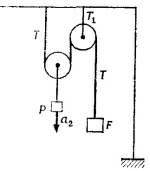
9.9. Нагрузка N на подвес, а следовательно, и на мачту и гондолу при таком способе перевозки марсиан определяется равенством
(Т—натяжение нити, Т1 — нагрузка на ось неподвижного блока); T1 равна сумме натяжений нити с одной и другой стороны неподвижного блока, т. е. Т1 = 2Т, так что N = 3T.
Запишем уравнения движения обоих марсиан:
(здесь g—ускорение марсианской силы тяжести). Так как веревка нерастяжима, то а1 и а2 связаны между собой. Очевидно, что при смещении оси подвижного блока вниз на х2 груз F поднимется на расстояние 2х2, т. е. 2х2 = —х1 (грузы смещаются в противоположные стороны). Дважды дифференцируя по времени это соотношение, называемое уравнением связи, получаем
Требуется решить уравнения движения совместно с полученным уравнением для ускорений. После простых подстановок имеем
В нашем случае Р = 90 кГ и F = 60 кГ, поэтому для N получаем 147 кГ.
Выигрыш в нагрузке на гондолу равен
 Гондольер Джузеппе мог бы получить значительно больший выигрыш в нагрузке, если бы поменял влюбленных местами. Нетрудно подсчитать, что в этом случае N= 116 кГ, а ΔN = 34 кГ, т. е. выигрыш в нагрузке увеличился бы примерно в 11 раз. Правда, в этом случае Паоло будет двигаться вниз с ускорением, в 3 раза превышающим то, с каким двигалась Франческа при первом способе перевозки, так что Джузеппе придется значительно увеличить скорость гондолы. Гондольер Джузеппе мог бы получить значительно больший выигрыш в нагрузке, если бы поменял влюбленных местами. Нетрудно подсчитать, что в этом случае N= 116 кГ, а ΔN = 34 кГ, т. е. выигрыш в нагрузке увеличился бы примерно в 11 раз. Правда, в этом случае Паоло будет двигаться вниз с ускорением, в 3 раза превышающим то, с каким двигалась Франческа при первом способе перевозки, так что Джузеппе придется значительно увеличить скорость гондолы.
9.10. Вес гири А на Луне меньше 1 кГ, поэтому камень В на блоке перетянет гирю. Запишем уравнения движения:
(gл — ускорение силы лунного тяготения, Т — натяжение нити), откуда
Кроме того, известно, что камень В растягивает пружину на Луне так же, как гиря А растягивает ее на Земле. Это означает, что mAg=mBgЛ, т. е. gЛ=(mA/mB)g (g—ускорение силы тяжести на Земле).
Подставляя это значение gЛ в выражение для а, после несложных преобразований получаем квадратное уравнение для тB:
(Второе решение квадратного уравнения тB = 1,34 кг отбрасываем, так как известно, что g/gЛ ≈ 6, поэтому должно быть и тB/тА ≈ 6.)
9.11. а) Чтобы найти ускорение лифта, запишем уравнение движения системы как целого
б) На груз М1 действуют две силы: натяжение нити и сила веса, причем M1a = T — M1g (масса M1 движется вверх с тем же ускорением а, что и лифт), т. е.
в) После обрыва нити иа массу М1 действует только сила тяжести, так что она движется вниз с ускорением g. Ускорение же лифта по-прежнему направлено вверх; величину его найдем из нового уравнения движения
г) Таким образом, мы убедились, что тело М1 движется вниз с ускорением g, а лифт поднимается вверх с ускорением a2. Значит, относительно лифта оно движется по направлению к полу с ускорением
9.12. Обозначим массу маляра через M1, а массу кресла через M2. Запишем уравнения движения маляра и кресла:
где Р—сила давления маляра на кресло.
Вычитая нижнее уравнение из верхнего, находим
9.13. Если груз М2 не опускается и не поднимается, то это означает, что его вес (M2g) равен натяжению нити. Найдем ускорение М1:
Определим теперь силу F. Так как М, M1 и М2 движутся как одно целое, то
9.14. Массы М и т движутся вправо как единое целое, поэтому (М+т)а = 2Т, где а — ускорение горизонтального движения, а Т — натяжение нити. Грузик m движется вертикально вниз с ускорением a1 уравнение его движения имеет вид ma1 = mg—Т.
Из рисунка, приведенного в условии задачи (стр. 29), видно, что при смещении рамы вправо на расстояние х грузик m опустится вниз на расстояние у = 2х, что дает a1 = 2a.
Таким образом,
В начальный момент времени грузик т1 покоился, поэтому время t, за которое он пройдет по вертикали расстояние d, можно найти из уравнения
К главе 10. Закон сохранения импульса
10.1. Пусть масса движущегося тела m, его скорость до соударения v0, а масса покоящегося тела хт (т. е. искомое отношение масс тел обозначено через х).
Рассмотрим сначала процесс столкновения двух тел не в неподвижной относительно Земли системе координат (будем называть ее лабораторной, или л-системой), а в системе центра масс (системе ц.м.):
В этой системе сумма импульсов тел равна нулю (т. е. в момент столкновения массы т и хт можно рассматривать как одно покоящееся тело). Отсюда сразу вытекает, что скорости тел т и хт обратно пропорциональны массам. Так как процесс абсолютно упругий, величины скоростей до и после удара одинаковы. Система ц.м. движется относительно Земли (т. е. относительно л-системы) с некоторой скоростью vц. Процесс столкновения в л-системе изображен на схеме слева. Столкновение в системе ц.м. можно наблюдать, если, скажем, сесть в машину, движущуюся вправо со скоростью vц. При этом вид из машины будет такой
Сравнивая эту картину с тем, что было сказано о столкновении в системе ц.м. ранее, получаем
Вычитая из третьего уравнения четвертое и деля получившееся выражение на второе уравнение, находим
откуда x = 3.
10.2. Рассмотрим сначала случай, когда скорости сталкивающихся тел одинаковы и равны v. После столкновения тела разлетаются с меньшими скоростями (v—Δv). Согласно
Обратимся теперь к случаю, когда одно из тел покоится, а другое движется со скоростью v. Перейдем в систему координат, движущуюся со скоростью v/2 в том же направлении, что и налетающее тело. Тем самым мы свели задачу к предыдущей, с той лишь разницей, что скорости сталкивающихся тел теперь уже не v, а v/2. Соответственно
т.е. после столкновения тела разлетаются со скоростями
Переходя в неподвижную систему координат, убеждаемся, что ранее неподвижное тело движется со скоростью
а налетевшее —с малой скоростью vf/4 в том же направлении, что и до соударения.
10.3. Двигаясь по орбите, спутник в единицу времени сталкивается с молекулами воздуха, занимающими объем vS (v — скорость спутника, S — площадь его поперечного сечения). Масса этого объема воздуха m1 = ρSv, где ρ—плотность воздуха.
Изменение количества движения спутника за этот же промежуток времени Δp = m(v—v′) равно, очевидно, изменению количества движения массы m1 воздуха, т. е.
(До столкновения средняя скорость молекулы воздуха относительно Земли равна нулю, после столкновения—скорости спутника v.)
Но изменение количества движения тела в единицу времени есть просто сила, действующая на тело. Таким образом, тормозящая сила Fторм = ρSv2, т. е. пропорциональна квадрату cкорости спутника. Найдем ее величину.
Для стационарной орбиты
(М и R—масса и радиус Земли, G—постоянная тяготения). Если тело находится на поверхности Земли, то, очевидно,
Подставляя это значение GM в выражение для скорости спутника, получаем
[Здесь мы воспользовались приближенной формулой: 1/ (1+х) ≈1–x при x«1.] Таким образом,
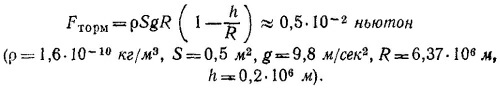 |
Как видно из формулы, связывающей высоту и скорость спутника, скорость спутника по мере уменьшения его высоты увеличивается. Может показаться странным, что действие силы торможения приводит к увеличению скорости. Однако дело состоит в том, что при наличии торможения скорость спутника уже не перпендикулярна к направлению силы тяжести, т. е. появляется составляющая силы тяжести, изменяющая величину скорости спутника. Ускоряющее действие этой составляющей превосходит тормозящее действие силы торможения.
10.4. а) Можно считать, что в самом начале движения масса ракеты остается все время постоянной и равной М0, т. е. можно пренебречь массой истекающих газов по сравнению с начальной массой ракеты. Кроме того, можно считать скорость газов относительно Земли постоянной и равной v0, так как скорость ракеты очень мала. Если вначале ракета покоилась, то количество движения ракеты вместе с топливом равно нулю. За время t из ракеты выбрасывается r0t кг газа со скоростью v0, сама ракета начинает двигаться со скоростью v в противоположном направлении. Из закона сохранения количества движения v0r0t=M0v, или v = (v0r0/M0) t. Ускорение же ракеты равно
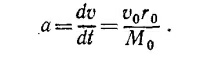 |
б) Силой тяги называется произведение массы ракеты на ускорение. Как было показано в пункте (а), это ускорение равно v0r0/M0, откуда F = v0r0. Следовательно, расход топлива для создания необходимой силы тяги есть
Мы здесь рассматривали силу тяги и расход топлива только в начальный момент времени. Ниже будет показано, что при постоянной относительной скорости истечения газов v0 сила тяги тоже постоянна, т. е. полученный результат справедлив в любой момент времени.
в) Пусть М —масса ракеты, a v—ее скорость в произвольный Момент времени t. За промежуток времени dt из ракеты будет выброшено r0 dt газов со скоростью (относительно Земли) v — v0, в результате чего скорость ракеты возрастет на dv. Согласно закону сохранения количества движения,
В левой части полученного уравнения стоит произведение массы ракеты в данный момент времени на ее ускорение dv/dt, следовательно, в правой части стоит сила F. Как видим, при постоянных r0 и v0 она также постоянна. Но М=М0—r0t, так что
Интегрируя правую и левую части, получаем зависимость скорости ракеты от времени
Интеграл, стоящий в правой части, можно найти в математическом справочнике. Во всяком случае, пользуясь приближенной формулой In (1 +х)≈ х при х«1, можно показать, что
Постоянная С определяется начальными условиями. Если при t = 0 ракета покоилась, то С = ln М0. Поэтому
10.5. Перейдем в систему координат, движущуюся со скоростью vц.м.. В этой системе скорости m1 и m2 будут соответственно v1—vц.м. и v2 — vц.м.. По определению системы ц.м.
10.6. Пусть имеется n тел с массами m1, т2 . . . , тn и скоростями v1, v2, ...., vn. В системе, движущейся со скоростью vц.м., скорости тел соответственно равны v1— vц.м., v2— vц.м....., vn— vц.м. а сумма импульсов равна нулю.
Собирая члены, содержащие vц.м., и перенося их в правую часть, в конце концов получаем
10.7. Скорости тел в неподвижной (лабораторной) системе координат обозначим v1 и v2, а в системе центра масс— v′1 и v′2 причем v′1=v1—vц.м. и v′2=v2—vц.м.. Кинетическая энергия этих тел в л-системе равна
Сумма первых двух членов есть кинетическая энергия тел в системе центра масс —Тц.м., а скобка при vц.м. равна нулю по определению системы ц.м. Таким образом,
10.8. Для произвольного числа тел формула для кинетической энергии будет иметь ту же структуру, что и в задаче 10.7. Коэффициент при vц.м, по той же причине, что и в задаче 10.7, будет равен нулю. Поэтому
10.9. Пусть скорость нейтрона до удара была v. Если масса нейтрона m, то масса ядра С12 равна примерно 12m. Закон сохранения количества движения дает
(v1—скорость нейтрона после столкновения, а v2 — скорость ядра). Согласно закону сохранения энергии, имеем
Мы выбираем в качестве v1 положительное решение квадратного уравнения, так как заранее знаем, что нейтрон полетит назад (из тех же соображений, что и в задаче 10.1). Направление скорости нейтрона после удара уже фактически учтено нами при записи закона сохранения импульса.
Для отношения кинетических энергий нейтрона до и после соударения получаем
 10.10. Найдем в первую очередь начальную скорость бруска v1. При этом можно воспользоваться законом сохранения импульса: пока брусок не отклонился, горизонтальные силы отсутствуют и поэтому импульс бруска с попавшей в него пулей равен начальному импульсу пули 10.10. Найдем в первую очередь начальную скорость бруска v1. При этом можно воспользоваться законом сохранения импульса: пока брусок не отклонился, горизонтальные силы отсутствуют и поэтому импульс бруска с попавшей в него пулей равен начальному импульсу пули
В точке наивысшего подъема кинетическая энергия бруска и пули 1/2(М+т) v12 переходит в потенциальную (M+m)gh, где h—высота подъема бруска, поэтому v12 = 2gh. Выразим h через х и L. Как видно из рисунка, треугольники АОС и АА′В подобны и h/x=x/2L, т. е. h = x2/2L.
Стало быть,
К главе 11. Векторы
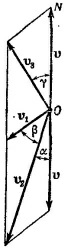 11.2. а) Велосипедиста обдувают два потока воздуха: встречный, движущийся со скоростью его собственного движения v, и косой— со скоростью v1. Естественно, велосипедист ощущает суммарный результат действия этих двух потоков, так что ему кажется, что ветер дует под углом α. Истинное же направление ветра (к направлению движения велосипедиста) составляет угол φ = α+β. Угол β найдем, принимая во внимание, что v2 = v1-+v, т. е. v1 v2 и v образуют треугольник. 11.2. а) Велосипедиста обдувают два потока воздуха: встречный, движущийся со скоростью его собственного движения v, и косой— со скоростью v1. Естественно, велосипедист ощущает суммарный результат действия этих двух потоков, так что ему кажется, что ветер дует под углом α. Истинное же направление ветра (к направлению движения велосипедиста) составляет угол φ = α+β. Угол β найдем, принимая во внимание, что v2 = v1-+v, т. е. v1 v2 и v образуют треугольник.
Для треугольника скоростей имеем
б) Если велосипедист движется на юг, то угол у между кажущимся направлением ветра и направлением движения велосипедиста удовлетворяет соотношению
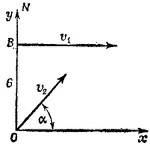 11.3. а) Выберем систему координат так, чтобы ось х была направлена строго на восток, а ось у—на север. Предположим далее, что второй корабль в начальный момент времени находится в начале координат О, а вектор его скорости v2 образует угол α с осью ОХ. Очевидно, первый корабль находится в точке В, лежащей на оси у на расстоянии 6 миль от О, а его скорость направлена параллельно оси х. 11.3. а) Выберем систему координат так, чтобы ось х была направлена строго на восток, а ось у—на север. Предположим далее, что второй корабль в начальный момент времени находится в начале координат О, а вектор его скорости v2 образует угол α с осью ОХ. Очевидно, первый корабль находится в точке В, лежащей на оси у на расстоянии 6 миль от О, а его скорость направлена параллельно оси х.
Таким образом изменение координат кораблей со временем дается выражениями
Квадрат расстояния между двумя кораблями, очевидно, равен
В условии задачи дано, что минимальное расстояние между кораблями равно 3 милям. Значит, к2 как функция времени t имеет минимум при некотором значении времени t = tмин. Но в этот момент времени производная от r2 обращается в нуль:
б) При меньшем значении угла α2 = 30° второй корабль проходит перед носом первого на расстоянии 3 миль, поэтому это значение угла должно быть исключено по условию задачи. Таким образом, второй корабль движется курсом строго на север и окажется на минимальном расстоянии от первого через tмин = 0,17 час от начального момента.
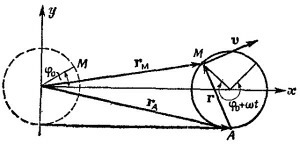 11.4. Можно считать, что произвольная точка М колеса участвует в двух движениях: равномерном со скоростью v вдоль оси х и вращательном вокруг центра колеса с угловой скоростью ω=v/R (см. задачу 8.12). Пусть в начальный момент времени t = 0 радиус-вектор точки М направлен под углом φ0 к оси х. Действуя точно так же, как и в задаче 8.12, находим координаты х и у точки М в произвольный момент времени t: 11.4. Можно считать, что произвольная точка М колеса участвует в двух движениях: равномерном со скоростью v вдоль оси х и вращательном вокруг центра колеса с угловой скоростью ω=v/R (см. задачу 8.12). Пусть в начальный момент времени t = 0 радиус-вектор точки М направлен под углом φ0 к оси х. Действуя точно так же, как и в задаче 8.12, находим координаты х и у точки М в произвольный момент времени t:
Компоненты скорости точки М найдем, дифференцируя по времени выражения для координат:
Будем считать, что в момент времени t точка М занимает положение, указанное на рисунке, а колесо соприкасается с горизонтальной поверхностью в точке А. Очевидно,
Непосредственными вычислениями убеждаемся в том, что скалярное произведение r·v = 0 (т. е. скорость точки М направлена перпендикулярно вектору r), а
Поскольку точка колеса М произвольна, полученный результат означает, что движение колеса в любой момент времени эквивалентно «чистому» вращению колеса с угловой скоростью ω вокруг мгновенной оси вращения, проходящей через точку соприкосновения колеса с горизонтальной плоскостью в тот же момент времени.
11.5. При движении против течения реки скорость лодки равна v — и, а по течению v+u. Поэтому время tv равно
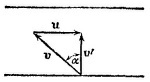 При движении поперек реки скорость лодки должна быть направлена под некоторым углом α к направлению на противоположный берег (иначе лодка не попадет в нужную точку). Скорость лодки поперек реки равна, как видно из рисунка, √v2—u2 поэтому время движения в поперечном направлении равно При движении поперек реки скорость лодки должна быть направлена под некоторым углом α к направлению на противоположный берег (иначе лодка не попадет в нужную точку). Скорость лодки поперек реки равна, как видно из рисунка, √v2—u2 поэтому время движения в поперечном направлении равно
Наконец, по озеру расстояние 2d лодка пройдет за время tL = 2d/v. Таким образом,
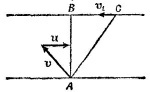 11.6. Обозначим скорость плывущего человека буквой v, скорость реки через и, а скорость ходьбы человека через v1 Чтобы попасть на противоположный берег в точку В, плывя под некоторым углом к течению, человеку потребуется время (см. предыдущую задачу) 11.6. Обозначим скорость плывущего человека буквой v, скорость реки через и, а скорость ходьбы человека через v1 Чтобы попасть на противоположный берег в точку В, плывя под некоторым углом к течению, человеку потребуется время (см. предыдущую задачу)
Если же он будет плыть перпендикулярно течению, то на противоположный берег он попадет за время t′2 = d/v, но течением его снесет в точку С, которая находится ниже В на расстоянии BC = ut′2.
Пешком это расстояние человек пройдет за время
поэтому полное время движения человека вторым способом равно
Таким образом, двигаясь вторым способом, человек попадет в точку В на 4 мин раньше.
11.7. Запишем сначала уравнение движения для клина M1. На этот клин действуют две силы: F и N1 — сила давления со стороны груза М, горизонтальная проекция которой равна N1(1/√2) и направлена против движения (фиг. 1). Итак,
Обратимся теперь к грузу М. Он скользит вверх по поверхности клина М2 (т. е. под углом 45° к горизонту) и в уравнение движения для этого груза входят поэтому лишь силы, действующие вдоль этого направления. Таких сил две: N1 и проекция силы тяжести Mg(1/√2). Имеем
Теперь нужно найти связь между а и а1. Как видно из фиг. 2, смещение груза М (изображена лишь нижняя кромка этого груза) вдоль поверхности клина М2 в √2 меньше смещения М1 по горизонтали. Следовательно, a = a1/√2.
Полученные уравнения запишем в виде системы
Умножая первое из этих уравнений на 2 и складывая правые и левые части, находим
Легко также найти силу N2; так как движения перпендикулярно поверхности М2 не происходит, то
Таким образом:
а) клин M1 движется горизонтально с ускорением 2g, направленным к неподвижной стенке;
б) груз М движется вверх вдоль неподвижного клина М2 с ускорением √2g;
в) сила давления клина М2 на груз М равна 272 кГ
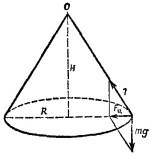 11.8. Пусть точка М движется по окружности радиусом R с постоянной скоростью v. Время одного оборота, т. е. период движения, есть Т = 2πR/v. К точке М приложены две силы: сила тяжести mg, направленная вертикально вниз, и сила натяжения нити Т, направленная вверх по нити. Очевидно, центростремительная сила Fц= mg+T; она направлена по радиусу горизонтальной окружности. Как видно (см. рисунок), модуль ее равен Fц = mg tg α, где α —угол между нитью и вертикалью, т. е. вызываемое этой силой центростремительное ускорение равно по величине g tg α. С другой стороны, оно, как известно, равно v2/R, поэтому v2/R = g tg α и v2 = gR tg α. 11.8. Пусть точка М движется по окружности радиусом R с постоянной скоростью v. Время одного оборота, т. е. период движения, есть Т = 2πR/v. К точке М приложены две силы: сила тяжести mg, направленная вертикально вниз, и сила натяжения нити Т, направленная вверх по нити. Очевидно, центростремительная сила Fц= mg+T; она направлена по радиусу горизонтальной окружности. Как видно (см. рисунок), модуль ее равен Fц = mg tg α, где α —угол между нитью и вертикалью, т. е. вызываемое этой силой центростремительное ускорение равно по величине g tg α. С другой стороны, оно, как известно, равно v2/R, поэтому v2/R = g tg α и v2 = gR tg α.
Таким образом,
11.9. а) Пусть имеется n тел с массами m1, ... , mn и скоростями v1............ vn. В системе ц. м. эти скорости соответственно равны v1—vц. м., ... , vn—vц. м.. По определению,
б) Обозначим через v′1, ..., vn скорости тел в системе ц. м. Тогда v1=v′1 + vц.м.,..., vn = v′n+vц. м. суть скорости тел в неподвижной системе координат. Кинетическая энергия в этой системе
11.10. Закон сохранения количества движения в векторной форме гласит
11.11. Кинетическая энергия частиц до столкновения равна
где v′1 и v′2 —скорости первой и второй частиц в системе ц. м. Обратим внимание, что вычисленная нами в предыдущей задаче скорость v есть фактически скорость центра масс vц. м.
Следовательно,
11.12. Выберем систему координат, в которой ось у направлена на север, а ось х —на восток. В этой системе координат скорость первого тела до и после удара есть
а) Скорость и2 более тяжелого тела после столкновения определим, пользуясь законом сохранения импульса:
относительная потеря энергии ΔT/T=3/4.
в) Согласно пункту (б), более легкое тело в системе ц. м. имело скорость до удара 4j, а после удара 2i. Это значит, что до удара оно двигалось вдоль оси у, а после удара—вдоль оси х. Следовательно, в системе ц. м. оно отклонилось на угол 90°.
11.13. Пусть v—скорость налетающей частицы. Найдем vц.м.:
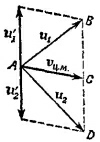 Начальные скорости частиц в системе ц.м. равны v′1 = v/2 и v′2 = —v/2. Начальные скорости частиц в системе ц.м. равны v′1 = v/2 и v′2 = —v/2.
После абсолютно упругого столкновения скорости частиц в системе ц. м. остаются прежними по величине (u′1 = u′2 = = v/2), но линия относительного движения поворачивается. Чтобы перейти к л-системе координат, нужно прибавить к векторам u′1 и u′2 вектор vц. м.. Соответствующее построение приведено на рисунке. Так как BC = AC = CD, через точки A, В и D можно провести окружность с центром в точке С. Следовательно, угол BAD — прямой (как вписанный угол, опирающийся на диаметр). Этот же результат можно получить и вычислениями. Пусть u′1 образует угол α с осью х. Тогда
Теперь легко убедиться, что u1·u2 = 0, откуда следует, что векторы u1 и u2 перпендикулярны друг другу.
Приведем также другое решение, при котором не нужно переходить в систему ц. м. Из закона сохранения импульса имеем
Возводя обе части этого равенства в квадрат
и вычитая из получившегося соотношения другое равенство, следствие закона сохранения энергии v2 =и12+ и22, находим u1·u2 = 0, т. е. векторы u1 и u2 перпендикулярны друг другу.
11.14. Уравнение движения для обоих шариков одно и то же: r = gk, где r —радиус-вектор любого из шариков. Общее решение этого уравнения имеет вид
где с1 и с2 —некоторые не зависящие от времени векторы. Они-то как раз и будут разными для разных шариков. Легко убедиться, что с1 равен радиусу-вектору частицы при t = 0, т. е. с1 = r(0), а с2, — равен начальной скорости частицы v (0). Следовательно,
11.15. Будем действовать по схеме, описанной в условии к задаче 11.13. Выберем ось х в направлении движения первой частицы, а ось у—перпендикулярно к ней вверх.
Очевидно, в л-системе скорости частиц равны
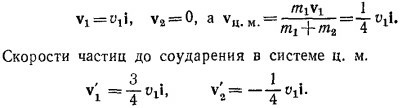 |
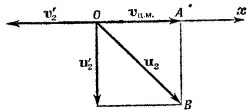 Так как соударение абсолютно упругое, в системе ц.м. скорости частиц по величине остались прежними, но линия относительного движения повернулась на некоторый угол. Чтобы понять, на какой именно угол повернулась эта линия, рассмотрим отдельно движение второй частицы в л-системе и системе ц.м. Так как соударение абсолютно упругое, в системе ц.м. скорости частиц по величине остались прежними, но линия относительного движения повернулась на некоторый угол. Чтобы понять, на какой именно угол повернулась эта линия, рассмотрим отдельно движение второй частицы в л-системе и системе ц.м.
В системе ц.м. частица двигалась со скоростью v′2 = vц.м. вдоль оси х (см. рисунок в условии задачи, стр. 37). С той же по величине скоростью она движется и после столкновения, только под некоторым углом к оси х, т. е. и′2 = vц.м. В л-системе u2= u′2+ vц.м. , причем угол между u2 и осью х равен 45°. Таким образом, треугольник ОАВ —равнобедренный с углами при основании по 45°; следовательно, угол OAB=90°.
Итак, линия относительного движения в системе ц.м. повернулась на угол 90°. Это значит, что вектор u′1 также направлен по оси у:
11.16. Пусть скорость тяжелой частицы до соударения v, а после соударения и. В системе ц.м. (vц.м. = Mv/(M+m)) модули этих скоростей равны
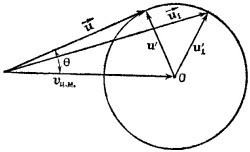 Направление вектора u′ произвольно, так что конец этого вектора описывает окружность радиусом mv/(M+m) < vц.м.. Поскольку u = u′ +vц.м. , простым геометрическим построением легко найти различные значения вектора u. Как видно из рисунка, угол отклонения налетающей частицы (направление начальной скорости v совпадает с направлением vц.м.) максимален в том случае, когда и направлено по касательной к окружности. При этом Направление вектора u′ произвольно, так что конец этого вектора описывает окружность радиусом mv/(M+m) < vц.м.. Поскольку u = u′ +vц.м. , простым геометрическим построением легко найти различные значения вектора u. Как видно из рисунка, угол отклонения налетающей частицы (направление начальной скорости v совпадает с направлением vц.м.) максимален в том случае, когда и направлено по касательной к окружности. При этом
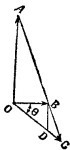 11.17. Выполнив для частицы массы m такое же построение, как и в предыдущей задаче (только теперь vц.м.=mv/(M+m), a u′m =Mν/(M+m), так что u′m > vц.м.), с учетом того, что угол между vц.м. и um равен 90°, определим u′m = um—vц.м. . Построим теперь на этом же рисунке u′M и uM [u′M = vц.м = mv/(M + m)]. Определим длину BD. Треугольники BDC и АОВ подобны, поэтому 11.17. Выполнив для частицы массы m такое же построение, как и в предыдущей задаче (только теперь vц.м.=mv/(M+m), a u′m =Mν/(M+m), так что u′m > vц.м.), с учетом того, что угол между vц.м. и um равен 90°, определим u′m = um—vц.м. . Построим теперь на этом же рисунке u′M и uM [u′M = vц.м = mv/(M + m)]. Определим длину BD. Треугольники BDC и АОВ подобны, поэтому
11.18. Задача решается так же, как и предыдущая, с тем лишь отличием, что и′m и и′M теперь уже не равны v′m и v′M. Скорости в системе ц.м. после соударения найдем из соотношения
Стало быть, отношение BD/OA остается тем же, что и в предыдущей задаче, но длина ОА меняется. В нашем случае ОА =v[√α2M2—m2/(М+m)]. Таким образом,
Если α=1 (абсолютно упругое соударение), этот результат переходит в результат предыдущей задачи. При уменьшении α уменьшается tg θ, а при α = m/М он обращается в нуль. Если α < m/М, полученная нами формула теряет смысл. Это и понятно: при столь малых значениях α и′m < vц.м.. поэтому рассеяние на прямой угол невозможно.
11.19. Если радиус-вектор частицы со временем меняется по закону
б) Действующую на частицу силу находим из уравнения движения:
в) Радиус кривизны траектории определяется как R = v2/a_. В нашем случае v2 = 1 +(1 +t)2 + (2/π2)2 cos2 π (t/2); дифференцируя по t, получаем
11.20. Используя решение задачи 11.14, можем сразу написать
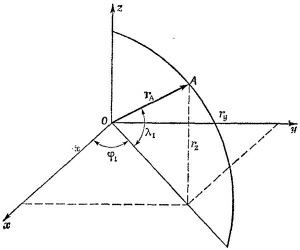 (ось z направлена вертикально вверх). (ось z направлена вертикально вверх).
11.21. Рассмотрим точку А на земной поверхности с координатами λ1 и φ1. Проведем из начала прямоугольной системы координат (выбранной так, как указано в примечании к условию задачи, стр. 38) радиус-вектор в точку А и найдем его компоненты:
где R — радиус Земли.
Аналогично, для другой точки с угловыми координатами (λ2, φ2) имеем
Длина дуги большого круга SAB, проходящего через рассматриваемые точки, равна ФR, где Ф —угол между векторами rA и rB. Этот угол найдем, вычислив скалярное произведение векторов rA и rB:
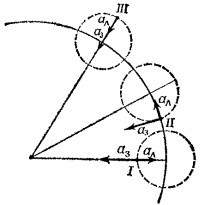 11.22. На рисунке схематически показано и отмечено цифрами I, II, III положение Луны в новолуние, первую четверть и полнолуние. 11.22. На рисунке схематически показано и отмечено цифрами I, II, III положение Луны в новолуние, первую четверть и полнолуние.
Рассмотрим движение Луны относительно Земли. Будем считать, что вокруг Земли Луна движется по круговой орбите, поэтому ее ускорение всегда направлено по радиусу орбиты к Земле.
Величина этого ускорения равна
где Rл — расстояние от Земли до Луны, а Тл — период обращения Луны.
В задаче 7.3 было показано, что
(Т3 — период обращения Земли вокруг Солнца, R3 — расстояние от Земли до Солнца, а М3 и МC — массы Земли и Солица).
Учитывая это, находим
Двигаясь вместе с Землей по круговой орбите вокруг Солнца, Луна обладает еще одним центростремительным ускорением, направленным по радиусу к Солнцу, величиной
(здесь мы пренебрегли RЛ но сравнению с R3). Таким образом, результирующее ускорение Луны по отношению к Солнцу в любой момент времени равно a =aЛ + a3. Поэтому
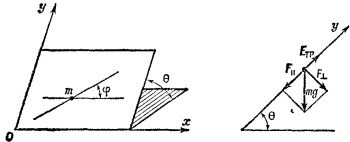 К главе 12. Характеристики сил К главе 12. Характеристики сил
12.1. Кирпич расположен на плоскости так, как показано на фиг. 1. Чтобы нагляднее изобразить силы, действующие на тело, нарисуем наклонную плоскость в другой проекции (фиг. 2). На тело действует сила веса mg, направленная вертикально вниз. Ее можно разложить на составляющие F|| и F_ вдоль и перпендикулярно наклонной плоскости. Первая вызывает движение вдоль оси у, вторая уравновешивается реакцией плоскости. Из треугольника сил находим эти силы:
а) При движении тела вверх (т.е. в положительном направлении оси у) уравнение движения имеет вид
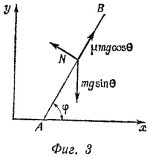 т. е. если μ≥tg θ, то скользить по наклонной плоскости только под действием силы тяжести кирпич не может. т. е. если μ≥tg θ, то скользить по наклонной плоскости только под действием силы тяжести кирпич не может.
в) Нарисуем для удобства плоскость ху так, чтобы она совпадала с плоскостью страницы. Составляющая силы Fll направлена вертикально вниз, a F_ —перпендикулярно рисунку за страницу.
Если кирпич скользит вниз по АВ, то сила трения направлена вверх по АВ, как показано на фиг. 3. Кроме того, к кирпичу приложена со стороны линейки сила, равная mg sin θ cos φ и направленная перпендикулярно линии АВ. Поэтому
Аналогично при движении кирпича вверх по АВ:
12.2. а) Пусть кирпич движется вверх по наклонной плоскости с начальной скоростью v0. Уравнение его движения имеет вид
где a1 = g(sin θ+ μ cos θ) (см. предыдущую задачу).
Через промежуток времени t1 = v0/а1 ≈ 0,45 сек (в этот момент времени его скорость v = v0 — a1t1 обратится в нуль) он достигнет наивысшей точки и пройдет по наклонной плоскости путь
б) Двигаясь вниз по наклонной плоскости с ускорением a2 = g(sinθ — μcos θ) (см. предыдущую задачу) и нулевой начальной скоростью, кирпич пройдет тот же путь S за время t2. Очевидно,
Полное время движения кирпича равно t1 + t2 =1,1 сек.
в) Кирпич теряет энергию на преодоление силы трения, поэтому изменение его кинетической энергии равно работе силы трения на пути 2S: ΔT = 2Sμmg cos θ ≈2,3 дж.
Этот же результат можно получить, вычислив непосредственно изменение кинетической энергии кирпича:
12.3. Рассмотрим сначала случай, когда сила Н направлена к склону. Вес W и приложенную внешнюю силу Н разлагаем на две составляющие: нормальную к наклонной плоскости и параллельную к ней. Как видно из рисунка (где показано разложение только силы Н),
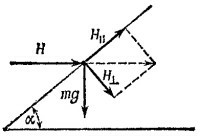 При достаточно большой силе H груз W начнет двигаться вверх по наклонной плоскости, так как H|| направлено вверх по плоскости, а в отсутствие силы H груз W покоится (μ >tg α). Непосредственно перед началом движения, когда к телу приложена сила Hмин, разность H||мин —W|| должна равняться силе трения. Последнюю получим, умножив силу нормального давления H_мин+ W_ на коэффициент трения μ. Итак, При достаточно большой силе H груз W начнет двигаться вверх по наклонной плоскости, так как H|| направлено вверх по плоскости, а в отсутствие силы H груз W покоится (μ >tg α). Непосредственно перед началом движения, когда к телу приложена сила Hмин, разность H||мин —W|| должна равняться силе трения. Последнюю получим, умножив силу нормального давления H_мин+ W_ на коэффициент трения μ. Итак,
Найдем теперь минимальное значение силы Н, направленной от наклонной плоскости, способной привести тело в движение. В этом случае тело W начнет двигаться вниз, а для минимальной силы записываем уравнение
Так как 3/(2—μ2) всегда больше 1/(2+μ2), во втором случае сила, приводящая в движение тело весом W, меньше.
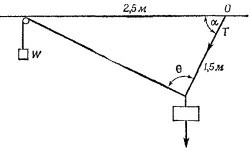 12.4. В точке О горизонтальная составляющая натяжения нити Т cos α уравновешивается силой трения, которая непосредственно перед началом скольжения кольца равна μТsin α. Таким образом, Т cos α = μТsin α, откуда tgα = 1/μ =4/3.После простых вычислений находим также, что sin α = 4/5. cosα = 3/5. По теореме синусов: 12.4. В точке О горизонтальная составляющая натяжения нити Т cos α уравновешивается силой трения, которая непосредственно перед началом скольжения кольца равна μТsin α. Таким образом, Т cos α = μТsin α, откуда tgα = 1/μ =4/3.После простых вычислений находим также, что sin α = 4/5. cosα = 3/5. По теореме синусов:
Спроектируем силы, действующие на груз весом 1 кГ, на направление перекинутой через блок нити. Сумма этих проекций должна быть равна нулю. Итак,
Аналогично, проектируя силы на направление нити длиной 1,5 м, находим T = 4/5кГ.
12.5. Пусть N — давление одной части замка на другую. Непосредственно перед началом движения FTp=μN. Так как части замка не движутся, сумма вертикальных проекций сил, действующих на часть А, так же как и горизонтальных, действующих на часть В, равна нулю. Поэтому
12.6. В системе, связанной с тележкой, на «неосторожного молодого человека» действует, кроме силы веса, псевдосила, равная —mа, где а —ускорение тележки (мы знаем, что его величина g sin α). Вертикальная составляющая ускорения равна gsin2α, поэтому весы будут показывать вес mg(1— sin2α) = mg cos2 α. Так как этот вес составляет 3/4 «настоящего» веса, то
12.7. Ускорение груза массы М2 обозначим через a2; направим его вертикально вверх. Ускорение a1 груза М1 (направление которого совпадает с поверхностью наклонной плоскости) связано с ускорением а2, как мы уже знаем, соотношением а1 = 2а2 (см., например, задачи 9.9, 9.14, 4.5).
Составим уравнения движения грузов M1 и M2:
Натяжение нити, прикрепленной к грузу M1 равно очевидно, Т/2 = 111 кГ.
12.8. Рассмотрим движение брусков непосредственно перед тем, как они начнут проскальзывать друг относительно друга. Запишем уравнение движения обоих брусков вместе, обозначив через μ1 коэффициент трения второго бруска о первый, а через μ2—бруска о наклонную плоскость:
здесь α — угол, который образует наклонная плоскость с горизонтом, причем sin α = 5/13 cos α = 12/13.
К верхнему бруску приложена только сила трения, равная (непосредственно перед началом проскальзывания) μ1m1g cos α. Под ее действием брусок движется с тем же самым ускорением а, что и нижний, поэтому
Наконец, величина силы F, соответствующая этому значению а, равна
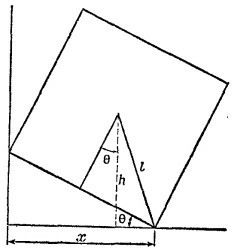 12.9. Пусть угол θ и коэффициент трения μ таковы, что куб, предоставленный сам себе, начинает скользить. При этом изменение его потенциальной энергии (за счет опускания ц. м.) окажется больше работы силы трения: за счет этой разницы и появляется кинетическая энергия у куба. Ясно, что в положении, когда силы трення едва хватает, чтобы удержать куб, изменение потенциальной энергии при (воображаемом) небольшом смещении куба будет как раз равно работе силы трения. Как видно из рисунка, высота ц. м. куба равна h = (l/√2) cos (45°— θ) (/ —длина ребра куба), а расстояние от нижнего ребра до стенки x = /cosθ. 12.9. Пусть угол θ и коэффициент трения μ таковы, что куб, предоставленный сам себе, начинает скользить. При этом изменение его потенциальной энергии (за счет опускания ц. м.) окажется больше работы силы трения: за счет этой разницы и появляется кинетическая энергия у куба. Ясно, что в положении, когда силы трення едва хватает, чтобы удержать куб, изменение потенциальной энергии при (воображаемом) небольшом смещении куба будет как раз равно работе силы трения. Как видно из рисунка, высота ц. м. куба равна h = (l/√2) cos (45°— θ) (/ —длина ребра куба), а расстояние от нижнего ребра до стенки x = /cosθ.
Если угол θ уменьшился на величину Δθ, то уменьшение потенциальной энергии куба равно
а работа силы трения равна μNl sin θΔθ, где N—сила давления куба на пол. Если угол θ такой, что куб все-таки не движется, то N = mg (сумма сил, действующих на куб, должна быть равна нулю). Итак,
Проверим, насколько разумен наш ответ. Предположим, что угол θ очень мал. Ясно, что в этом случае нужно очень большое трение, чтобы удержать куб от скольжения. Это видно и из нашей формулы (при θ →0 μ→ ∞). Если θ = 45°, куб балансирует на нижнем ребре и нужна очень маленькая сила со стороны стенки и соответственно очень маленькая сила трения, чтобы удержать его (при θ = 45° μ = 0). Наконец, если μ=1, куб будет в равновесии при θ = 18°30′.
12.10. Обозначим через N1 и N2 силы нормального давления, возникающие в верхнем и нижнем соединениях кронштейна со столбом, а через F1(тр) и F2(тр) — силы трения в этих же соединениях. Так как кронштейн находится в равновесии, то проекции всех сил на горизонтальное и вертикальное направления равны нулю. Поэтому
(Р —вес кронштейна).
Непосредственно перед тем, как кронштейн начнет соскальзывать по столбу, силы трения (направленные вверх, что учтено при записи второго уравнения) равны
Учитывая это и вводя обозначение N1 = N2=N, вместо системы двух уравнений получаем 51P = 0,6N.
Еще одно уравнение для Р и N получаем, используя принцип виртуальных перемещений.
Поворачивая кронштейн как целое на малый угол Δφ, например, вокруг точки О, убеждаемся (см. задачи к гл. 4), что любая точка кронштейна, находящаяся на расстоянии I от оси вращения, при этом смещается влево на расстояние / cos φΔφ и вниз —на / sin φΔφ. Но / cos φ — расстояние до данной точки от оси вращения по вертикали, a I sin φ—расстояние по горизонтали, поэтому закон сохранения энергии при выбранном виртуальном перемещении записывается в виде
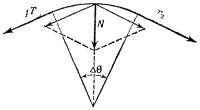 12.11. а) Если веревка подвинется вправо на расстояние S, то при этом будет выполнена работа ΔTS. Эта работа должна равняться работе сил трення 12.11. а) Если веревка подвинется вправо на расстояние S, то при этом будет выполнена работа ΔTS. Эта работа должна равняться работе сил трення
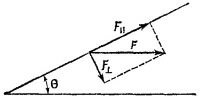 12.12. Перейдем в систему координат, жестко связанную с полосой. В этой системе на тело действует псевдосила F=ma. Разложим ее на две составляющие: F|| вдоль полосы и F_ — перпендикулярно к ней. Они равны соответственно (см. рисунок) 12.12. Перейдем в систему координат, жестко связанную с полосой. В этой системе на тело действует псевдосила F=ma. Разложим ее на две составляющие: F|| вдоль полосы и F_ — перпендикулярно к ней. Они равны соответственно (см. рисунок)
Уравнение движения в выбранной нами системе координат имеет вид (ось х направлена вверх по полосе)
Путь S тело проходит за время (начальная скорость тела равна нулю)
12.13. а) В гл. 12 «Лекций» (вып. 1) показано, что на заряд q, помещенный в электрическое поле напряженностью Е, действует сила F, равная qE, причем F измеряется в ньютонах, a q—в кулонах. Отсюда
(символ [А] означает размерность физической величины А).
б) На заряд q, движущийся в магнитном поле со скоростью v, действует сила
Обратите внимание, что так называемая скорость дрейфа частиц в скрещенном электрическом и магнитном полях равна как раз этому отношению (подробнее см. «Лекции», вып. 6, стр. 340 или задачу 12.16).
г) Для гравитационного поля С:
12.14. Пусть частица движется в плоскости ху, а магнитная индукция направлена по оси z. На частицу действует сила, компоненты которой
Как было показано в задаче 9.1, под действием такой силы частица равномерно движется по круговой орбите, лежащей в плоскости ху, причем радиус орбиты равен R=mv/qB.
12.15. Так как частица движется равномерно по круговой орбите, то время одного оборота Т найдем по формуле
(в предыдущей задаче показано, что R = mv/qB).
При ускорении частицы в циклотроне необходимо точно знать время Т, чтобы правильно выбрать частоту ускоряющего электрического поля. Период колебаний этого поля должен совпадать с периодом обращения частицы (так называемое условие резонанса, или синхронизма).
12.16. а) Уравнение движения частицы в данном электромагнитном поле есть [см. формулу (12.11) «Лекций», вып. 1, стр. 224]
получаем следующие уравнения движения в штрихованной системе:
Как следует из уравнений движения, в штрихованной системе координат частица будет двигаться по круговой орбите в плоскости х′у′ радиусом R = mv/qBz.
Из преобразований Галилея видно, что штрихованная система координат движется в положительном направлении оси х нештрихованной системы со скоростью vd = Ey/Bz.
(Скорость vd называют скоростью дрейфа.) Значит, в нештрихованной системе координат частица движется по циклоиде (сравните с задачей 8.12).
К главе 14. Работа и потенциальная энергия
14.1
14.2. Приближенно можно положить
Продолжение. Решения и ответы к задачам I-IV томов фейнмановских лекций по физике
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|




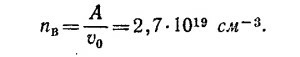
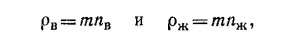
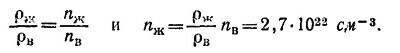
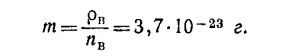
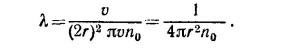
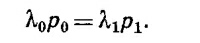
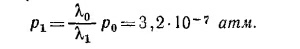
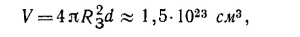
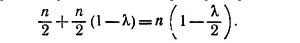
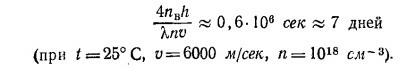
 1.5. Рассмотрим часть грани кристалла. Расположение атомов в кристалле таково, что каждый атом окружен определенным образом расположенными другими атомами. Это означает, что атомы одного сорта расположены в так называемых эквивалентных точках, т. е, точках, окружение которых совершенно одинаково. Минимальное расстояние между эквивалентными точками а называется периодом решетки.
1.5. Рассмотрим часть грани кристалла. Расположение атомов в кристалле таково, что каждый атом окружен определенным образом расположенными другими атомами. Это означает, что атомы одного сорта расположены в так называемых эквивалентных точках, т. е, точках, окружение которых совершенно одинаково. Минимальное расстояние между эквивалентными точками а называется периодом решетки. Приведем доказательство от противного. Пусть ячейка кристалла—правильный пятиугольник, а О и А—эквивалентные точки (фиг. 2). Очевидно, эквивалентной должна быть и точка Е (если эквивалентная точка помещается на расстоянии а от О при перемещении вправо, то должна быть эквивалентная точка и при перемещении влево на то же расстояние). Другие эквивалентные точки можно построить, поворачивая отрезок О А на угол 2π/5 = 72°. После первого поворота получим точку В, а после второго—точку С. Но расстояние ЕС < а, что противоречит исходному предположению (расстояние между эквивалентными точками не меньше, чем а). Таким образом, грань кристалла не может быть правильным пятиугольником. Можно строго показать, что аналогичное построение непротиворечиво только в том случае, если ячейки кристалла имеют форму правильного треугольника, четырехугольника (квадрата) и шестиугольника.
Приведем доказательство от противного. Пусть ячейка кристалла—правильный пятиугольник, а О и А—эквивалентные точки (фиг. 2). Очевидно, эквивалентной должна быть и точка Е (если эквивалентная точка помещается на расстоянии а от О при перемещении вправо, то должна быть эквивалентная точка и при перемещении влево на то же расстояние). Другие эквивалентные точки можно построить, поворачивая отрезок О А на угол 2π/5 = 72°. После первого поворота получим точку В, а после второго—точку С. Но расстояние ЕС < а, что противоречит исходному предположению (расстояние между эквивалентными точками не меньше, чем а). Таким образом, грань кристалла не может быть правильным пятиугольником. Можно строго показать, что аналогичное построение непротиворечиво только в том случае, если ячейки кристалла имеют форму правильного треугольника, четырехугольника (квадрата) и шестиугольника. 1.11. Посмотрим, как разместятся шарики при наиболее плотной упаковке (как раз тогда в сосуде поместится максимальное число шариков). Первый слой шариков ляжет так, что каждый шарик соприкоснется с шестью другими (положение центров шариков этого слоя показано на рис. а черными точками). Шарики второго слоя лягут в «ямки» первого слоя, так что каждый шарик второго слоя соприкоснется с тремя шариками нижнего (обратите внимание, что используется только половина «ямок» первого слоя), а в остальном второй слой выглядит точно так же, как первый, только смещен относительно него в вертикальном направлении. Центры шариков второго слоя, если смотреть на них сверху, займут положение, обозначенное на рис. а светлыми кружочками. Третий слой шариков можно наложить двумя разными способами: шарики могут лечь в те «ямки» второго слоя, которые находятся над центрами шариков нижнего слоя, тогда получится, что шарики третьего слоя лежат точно над шариками первого слоя (центры шаров верхнего слоя обозначены крестиками). Если же шарики третьего слоя лягут в другие «ямки» второго слоя, то окажется, что они будут находится как раз над «свободными ямками» первого слоя (рис. б). Плотность упаковки и в том и в другом случаях одинакова, т. е. число шариков в единице объема в обоих случаях одинаково.
1.11. Посмотрим, как разместятся шарики при наиболее плотной упаковке (как раз тогда в сосуде поместится максимальное число шариков). Первый слой шариков ляжет так, что каждый шарик соприкоснется с шестью другими (положение центров шариков этого слоя показано на рис. а черными точками). Шарики второго слоя лягут в «ямки» первого слоя, так что каждый шарик второго слоя соприкоснется с тремя шариками нижнего (обратите внимание, что используется только половина «ямок» первого слоя), а в остальном второй слой выглядит точно так же, как первый, только смещен относительно него в вертикальном направлении. Центры шариков второго слоя, если смотреть на них сверху, займут положение, обозначенное на рис. а светлыми кружочками. Третий слой шариков можно наложить двумя разными способами: шарики могут лечь в те «ямки» второго слоя, которые находятся над центрами шариков нижнего слоя, тогда получится, что шарики третьего слоя лежат точно над шариками первого слоя (центры шаров верхнего слоя обозначены крестиками). Если же шарики третьего слоя лягут в другие «ямки» второго слоя, то окажется, что они будут находится как раз над «свободными ямками» первого слоя (рис. б). Плотность упаковки и в том и в другом случаях одинакова, т. е. число шариков в единице объема в обоих случаях одинаково. К главе 4. Сохранение энергии
К главе 4. Сохранение энергии 4.2. Введем следующие обозначения: F1— сила давления роликов на вертикальную стену; F2 и F3— горизонтальная и вертикальная составляющие силы давления лестницы на землю. Очевидно, что F1 направлена налево, F2— направо, а F3— вниз. Силы, приложенные к лестнице, равны по величине F1 F2 и F3 и направлены в противоположных направлениях.
4.2. Введем следующие обозначения: F1— сила давления роликов на вертикальную стену; F2 и F3— горизонтальная и вертикальная составляющие силы давления лестницы на землю. Очевидно, что F1 направлена налево, F2— направо, а F3— вниз. Силы, приложенные к лестнице, равны по величине F1 F2 и F3 и направлены в противоположных направлениях.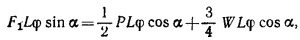
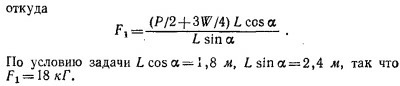
 4.3. Уравновесим стержень подъемного устройства грузом Т, подвешенным на малом блоке в точке С. При виртуальном повороте стержня по часовой стрелке на малый угол φ вокруг нижнего конца точка М стержня, находящаяся на расстоянии / от оси вращения, опустится вниз на расстояние lφ sin θ и сместится вправо на lφcos θ (см. предыдущую задачу). Поэтому при таком перемещении потенциальная энергия стержня и груза W уменьшится на (W + 1/2w) ·Lφ sin θ, а груз Т, как видно из рисунка, поднимется на высоту xφcos θ, т. е. его потенциальная энергия увеличится на Txφcos θ. Из закона сохранения энергии
4.3. Уравновесим стержень подъемного устройства грузом Т, подвешенным на малом блоке в точке С. При виртуальном повороте стержня по часовой стрелке на малый угол φ вокруг нижнего конца точка М стержня, находящаяся на расстоянии / от оси вращения, опустится вниз на расстояние lφ sin θ и сместится вправо на lφcos θ (см. предыдущую задачу). Поэтому при таком перемещении потенциальная энергия стержня и груза W уменьшится на (W + 1/2w) ·Lφ sin θ, а груз Т, как видно из рисунка, поднимется на высоту xφcos θ, т. е. его потенциальная энергия увеличится на Txφcos θ. Из закона сохранения энергии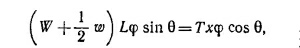
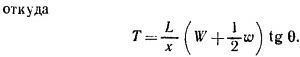
 4.4. а) Представим себе, что стержень АВ фермы удален. Тогда под действием груза W шарнир В пойдет вниз направо, а шарнир А — вверх налево. Ясно поэтому, что стержень АВ был растянут. Однако и удалив стержень, мы тоже можем удержать ферму в равновесии, подвесив два равных груза на неподвижных блоках так, как это показано на рисунке. Если длина АВ увеличивается, грузы поднимаются и их потенциальная энергия возрастает. Чтобы потенциальная энергия всей системы оставалась неизменной, груз W должен опуститься. Следовательно, при нагревании стержня АВ груз W опускается,
4.4. а) Представим себе, что стержень АВ фермы удален. Тогда под действием груза W шарнир В пойдет вниз направо, а шарнир А — вверх налево. Ясно поэтому, что стержень АВ был растянут. Однако и удалив стержень, мы тоже можем удержать ферму в равновесии, подвесив два равных груза на неподвижных блоках так, как это показано на рисунке. Если длина АВ увеличивается, грузы поднимаются и их потенциальная энергия возрастает. Чтобы потенциальная энергия всей системы оставалась неизменной, груз W должен опуститься. Следовательно, при нагревании стержня АВ груз W опускается,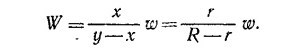
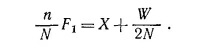
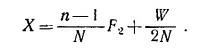
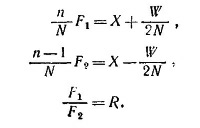
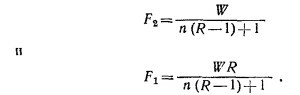
 4.8. Выберем такое виртуальное перемещение цепи, при котором она опускается на расстояние Н вниз по вертикали параллельно самой себе. Потенциальная энергия ее при этом уменьшится на WH. Радиус же цепи при таком перемещении увеличится на величину а. Легко сообразить, что увеличение радиуса цепи и ее смещение вниз связаны соотношением a/H=r/h. Если натяжение цепи обозначить через Т, то виртуальная работа сил натяжения при рассматриваемом виртуальном перемещении цепи равна
4.8. Выберем такое виртуальное перемещение цепи, при котором она опускается на расстояние Н вниз по вертикали параллельно самой себе. Потенциальная энергия ее при этом уменьшится на WH. Радиус же цепи при таком перемещении увеличится на величину а. Легко сообразить, что увеличение радиуса цепи и ее смещение вниз связаны соотношением a/H=r/h. Если натяжение цепи обозначить через Т, то виртуальная работа сил натяжения при рассматриваемом виртуальном перемещении цепи равна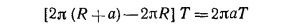
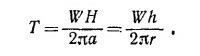
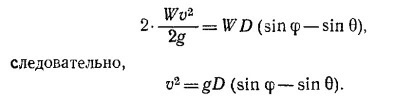
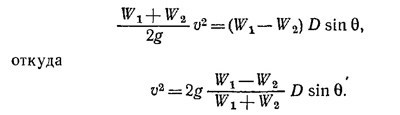
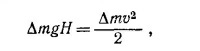
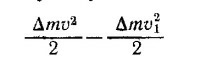
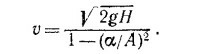
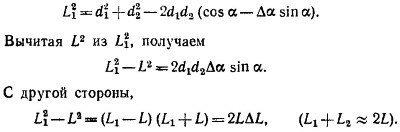
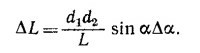
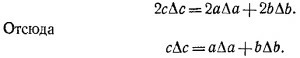
 4.14. Пронумеруем бревна, как показано на рисунке. Пусть бревно 2 при небольшом уменьшении угла θ начнет двигаться вниз, выталкивая бревно 3 вверх по кузову. Ясно, что в конце движения бревно 2 займет положение бревна 3, а бревно 3—положение, показанное на рисунке пунктиром. Так как при первоначальном расположении бревна находились в равновесии, изменение потенциальной энергии бревен при рассмотренных перемещениях должно равняться нулю. Это возможно только в том случае, если центр бревна 2 в первом и центр бревна 3 во втором случаях находятся на одной и той же высоте. Обозначим указанные высоты через y1 и y2 соответственно. Вычисление у2 не вызывает никаких затруднений. Непосредственно из рисунка видно, что y2= R cos θ + 5R sin θ, где R — радиус бревна.
4.14. Пронумеруем бревна, как показано на рисунке. Пусть бревно 2 при небольшом уменьшении угла θ начнет двигаться вниз, выталкивая бревно 3 вверх по кузову. Ясно, что в конце движения бревно 2 займет положение бревна 3, а бревно 3—положение, показанное на рисунке пунктиром. Так как при первоначальном расположении бревна находились в равновесии, изменение потенциальной энергии бревен при рассмотренных перемещениях должно равняться нулю. Это возможно только в том случае, если центр бревна 2 в первом и центр бревна 3 во втором случаях находятся на одной и той же высоте. Обозначим указанные высоты через y1 и y2 соответственно. Вычисление у2 не вызывает никаких затруднений. Непосредственно из рисунка видно, что y2= R cos θ + 5R sin θ, где R — радиус бревна.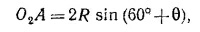
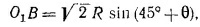
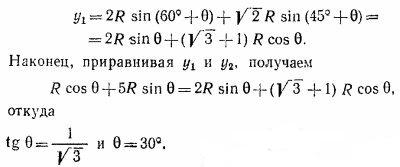

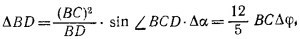
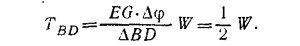
 4.16. Если стержень находится в равновесии, то, повернув его на малый угол Δφ около точки Р, мы должны обнаружить, что потенциальная энергия не изменилась. Зто означает, что потенциальная энергия одного из кусков увеличивается, а другого уменьшается, в точности компенсируя это увеличение. Так как потенциальная энергия однородного стержня зависит от высоты его середины, нужно определить, как изменятся высоты середин кусков при повороте на угол Δφ (см. рисунок). Как видно из рисунка (для удобства треугольники ВВ′В″ и СС′С″ нарисованы отдельно), середина куска весом 2W опустится на величину B′B″=sin α1·BB′ а середина куска весом W поднимется на С′С″ = sin α2·CC′, Итак,
4.16. Если стержень находится в равновесии, то, повернув его на малый угол Δφ около точки Р, мы должны обнаружить, что потенциальная энергия не изменилась. Зто означает, что потенциальная энергия одного из кусков увеличивается, а другого уменьшается, в точности компенсируя это увеличение. Так как потенциальная энергия однородного стержня зависит от высоты его середины, нужно определить, как изменятся высоты середин кусков при повороте на угол Δφ (см. рисунок). Как видно из рисунка (для удобства треугольники ВВ′В″ и СС′С″ нарисованы отдельно), середина куска весом 2W опустится на величину B′B″=sin α1·BB′ а середина куска весом W поднимется на С′С″ = sin α2·CC′, Итак,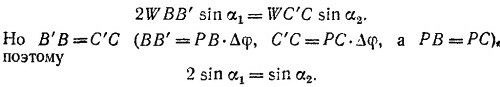
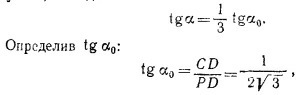
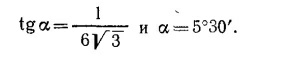
 4.17. Грузы W1 и W2 на проволочной рамке можно уравновесить, подвесив на двух блоках два других груза весом Т каждый (Т — натяжение нити), как показано на рисунке. Пусть груз W2 сдвинется на небольшое расстояние Δx2 вниз по проволоке, а груз W1 останется неподвижным. При таком перемещении груз W2 опустится по вертикали на расстояние Δx2 cos 30°, а грузы Т поднимутся вверх на величину Δ/ = Δx2 cos (90s—α) (Δ/ — удлинение нити при выбранном виртуальном перемещении). Согласно закону сохранения энергии
4.17. Грузы W1 и W2 на проволочной рамке можно уравновесить, подвесив на двух блоках два других груза весом Т каждый (Т — натяжение нити), как показано на рисунке. Пусть груз W2 сдвинется на небольшое расстояние Δx2 вниз по проволоке, а груз W1 останется неподвижным. При таком перемещении груз W2 опустится по вертикали на расстояние Δx2 cos 30°, а грузы Т поднимутся вверх на величину Δ/ = Δx2 cos (90s—α) (Δ/ — удлинение нити при выбранном виртуальном перемещении). Согласно закону сохранения энергии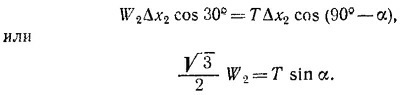
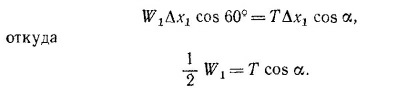
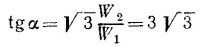
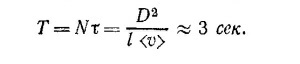
 6.3.Обозначим через р расстояние от центра шарика до оси, проходящей через центр неподвижной сферы параллельно скорости шарика (так называемый прицельный параметр). Как видно из рисунка, p = (a + b)sinα, где α—угол между скоростью шарика и радиусом сферы, проведенным в точку попадания шарика, т. е. угол падения. Введем угол рассеяния x — угол между начальной и конечной скоростями
6.3.Обозначим через р расстояние от центра шарика до оси, проходящей через центр неподвижной сферы параллельно скорости шарика (так называемый прицельный параметр). Как видно из рисунка, p = (a + b)sinα, где α—угол между скоростью шарика и радиусом сферы, проведенным в точку попадания шарика, т. е. угол падения. Введем угол рассеяния x — угол между начальной и конечной скоростями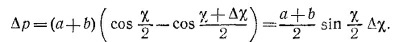
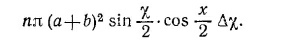
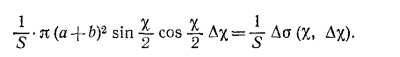
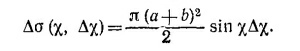
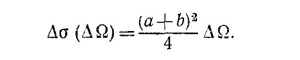
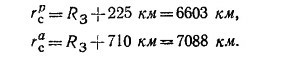
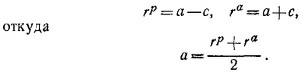
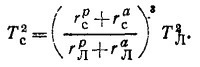
 В нашем случае это дает Tс=1,55 час.
В нашем случае это дает Tс=1,55 час.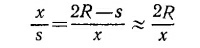
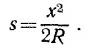
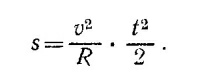
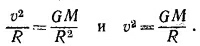
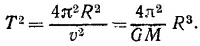
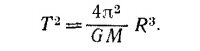
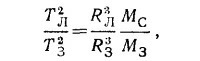
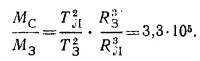
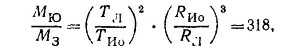
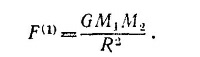
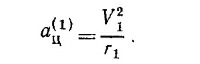
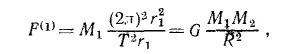
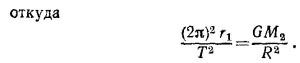
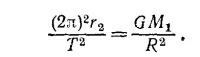
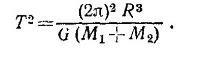
 Полученная формула показывает, что период обращения тел зависит только от расстояния между ними и их суммарной массы (а не массы каждого из тел или же отношения их масс).
Полученная формула показывает, что период обращения тел зависит только от расстояния между ними и их суммарной массы (а не массы каждого из тел или же отношения их масс).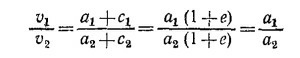
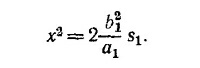
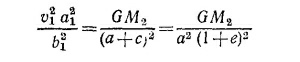
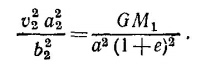
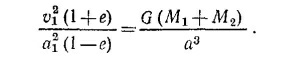
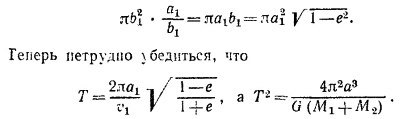
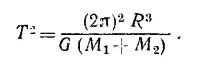
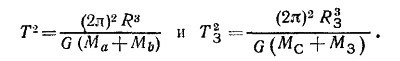
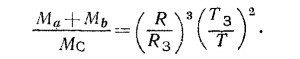
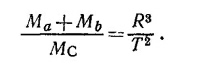
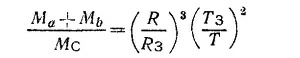
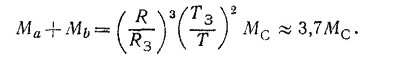
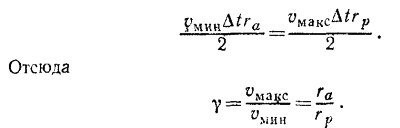
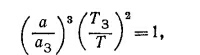
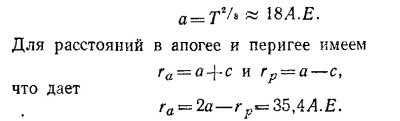
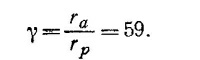
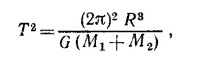
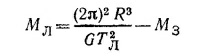
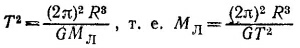

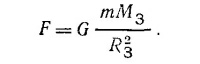
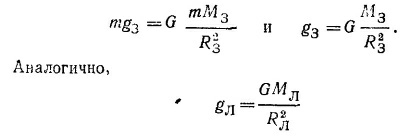
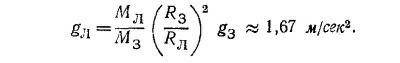
 7.11. Пусть лаборатория, где производится эксперимент, расположена в точке С Земли. На тела, находящиеся в лаборатории, действуют силы притяжения Земли и Луны, причем эти силы вычитаются, если Луна находится в точке А, или складываются, если Луна находится в точке В. Ускорение свободного падения для этих двух случаев равно
7.11. Пусть лаборатория, где производится эксперимент, расположена в точке С Земли. На тела, находящиеся в лаборатории, действуют силы притяжения Земли и Луны, причем эти силы вычитаются, если Луна находится в точке А, или складываются, если Луна находится в точке В. Ускорение свободного падения для этих двух случаев равно
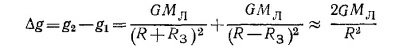
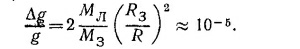
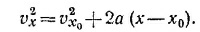
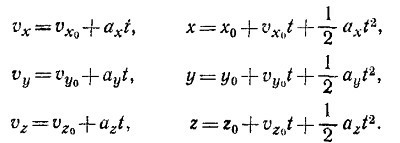
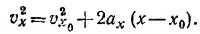
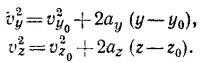
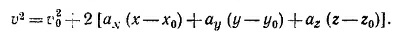
 8.4. Обозначим расстояние, которое пролетит снаряд по горизонтали, через S, а максимальную высоту его полета —через H. В начальный момент времени (t = 0), х0=0, у0 = 0, а vx0 = v cos θ, vy0 = v sin θ (см. § 5 гл. 8 «Лекций», вып, 1, стр. 152). Используя результаты задачи 8.3, находим
8.4. Обозначим расстояние, которое пролетит снаряд по горизонтали, через S, а максимальную высоту его полета —через H. В начальный момент времени (t = 0), х0=0, у0 = 0, а vx0 = v cos θ, vy0 = v sin θ (см. § 5 гл. 8 «Лекций», вып, 1, стр. 152). Используя результаты задачи 8.3, находим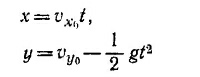
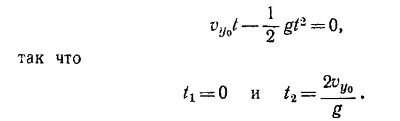
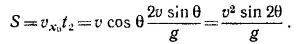
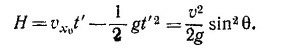
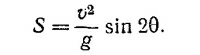
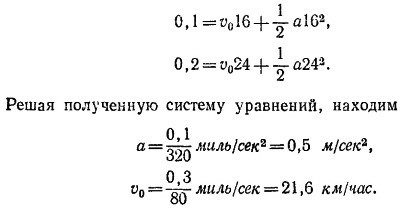
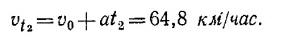
 8.7. а) В промежуток времени от t0 = 0 до t1 = 50 сек, т. е. во время работы двигателя, ракета двигалась с ускорением 2g. Значит, в этом интервале времени скорость ракеты определяется формулой
8.7. а) В промежуток времени от t0 = 0 до t1 = 50 сек, т. е. во время работы двигателя, ракета двигалась с ускорением 2g. Значит, в этом интервале времени скорость ракеты определяется формулой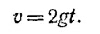
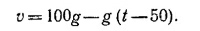
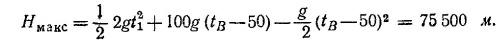
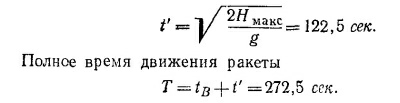

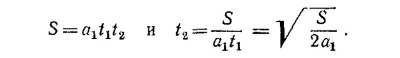
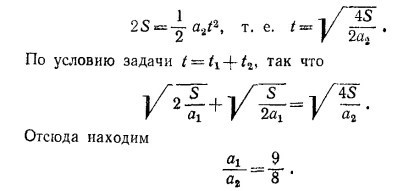
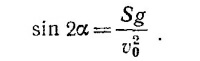
 8.10. а) Известно, что θ = S/R. По определению sin θ = AC/R, а cos θ = OC/R. При малых углах θ дугу АВ можно заменить перпендикуляром АС, а ОС — радиусом R. В этом случае sin θ ≈ S/R = θ и cos θ ≈ R/R = 1
8.10. а) Известно, что θ = S/R. По определению sin θ = AC/R, а cos θ = OC/R. При малых углах θ дугу АВ можно заменить перпендикуляром АС, а ОС — радиусом R. В этом случае sin θ ≈ S/R = θ и cos θ ≈ R/R = 1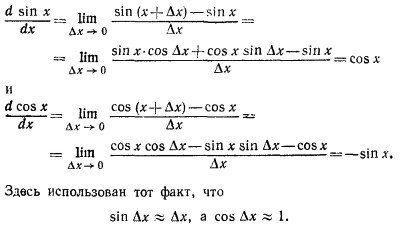
 8.11. а) Пусть тело в момент времени t окажется в точке М (х, у) окружности. Обозначим через φ угол между радиусом этой точки и положительным направлением оси х. Как видно из рисунка, координаты этой точки:
8.11. а) Пусть тело в момент времени t окажется в точке М (х, у) окружности. Обозначим через φ угол между радиусом этой точки и положительным направлением оси х. Как видно из рисунка, координаты этой точки: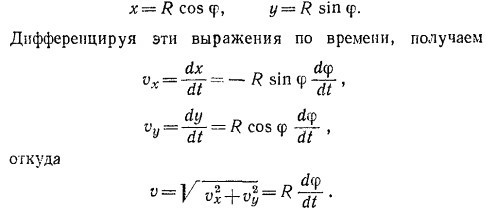
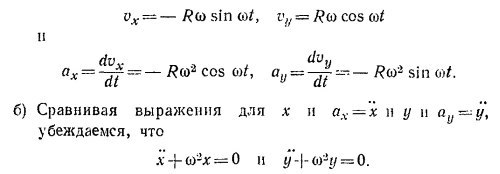
 8.12. Координату х камешка удобно представить в виде суммы х = х′ +х″, где х′—координата относительно оси колеса, а х″—координата оси колеса (см. рисунок). Выражение для х′ и у′ получены в предыдущей задаче (мы должны лишь заменить в соответствующих формулах ωt на —ωt, так как, когда колесо катится в положительном направлении оси х, оно вращается по часовой стрелке, а в предыдущей задаче рассмотрено вращение против часовой стрелки). Итак,
8.12. Координату х камешка удобно представить в виде суммы х = х′ +х″, где х′—координата относительно оси колеса, а х″—координата оси колеса (см. рисунок). Выражение для х′ и у′ получены в предыдущей задаче (мы должны лишь заменить в соответствующих формулах ωt на —ωt, так как, когда колесо катится в положительном направлении оси х, оно вращается по часовой стрелке, а в предыдущей задаче рассмотрено вращение против часовой стрелки). Итак,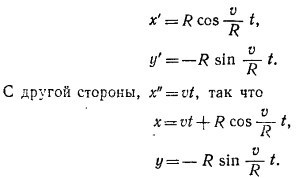
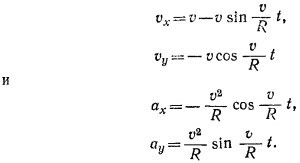
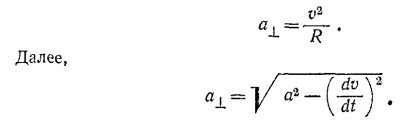

 9.3. а) Мяч влетел в окно горизонтально; это означает, что окно находилось в наивысшей точке траектории мяча. Максимальная же высота подъема определяется по формуле (см. задачу 8.4)
9.3. а) Мяч влетел в окно горизонтально; это означает, что окно находилось в наивысшей точке траектории мяча. Максимальная же высота подъема определяется по формуле (см. задачу 8.4)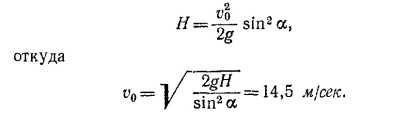
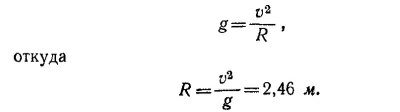

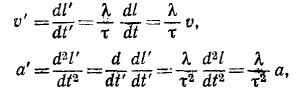
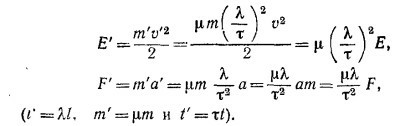
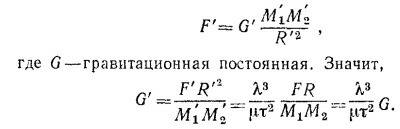
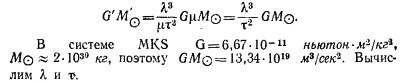
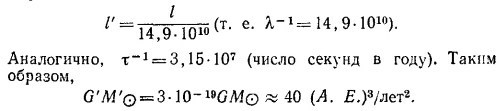
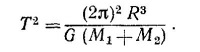
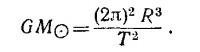
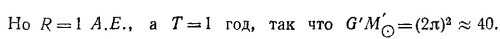
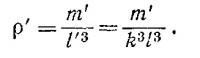
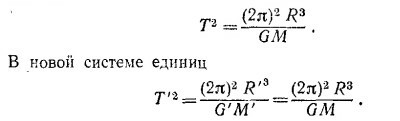
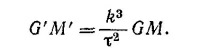
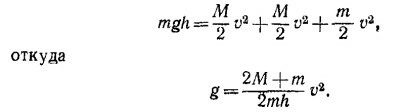
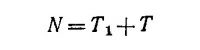
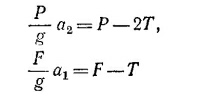
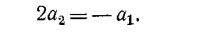
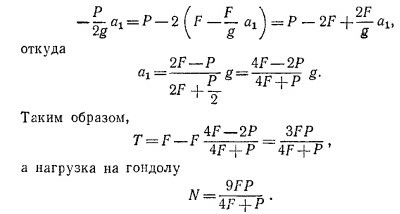
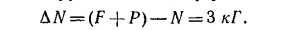
 Гондольер Джузеппе мог бы получить значительно больший выигрыш в нагрузке, если бы поменял влюбленных местами. Нетрудно подсчитать, что в этом случае N= 116 кГ, а ΔN = 34 кГ, т. е. выигрыш в нагрузке увеличился бы примерно в 11 раз. Правда, в этом случае Паоло будет двигаться вниз с ускорением, в 3 раза превышающим то, с каким двигалась Франческа при первом способе перевозки, так что Джузеппе придется значительно увеличить скорость гондолы.
Гондольер Джузеппе мог бы получить значительно больший выигрыш в нагрузке, если бы поменял влюбленных местами. Нетрудно подсчитать, что в этом случае N= 116 кГ, а ΔN = 34 кГ, т. е. выигрыш в нагрузке увеличился бы примерно в 11 раз. Правда, в этом случае Паоло будет двигаться вниз с ускорением, в 3 раза превышающим то, с каким двигалась Франческа при первом способе перевозки, так что Джузеппе придется значительно увеличить скорость гондолы.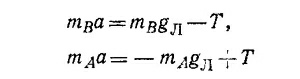
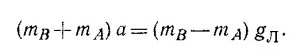
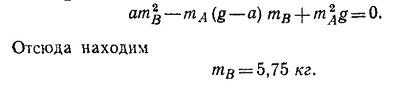
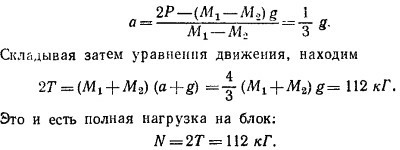
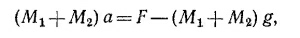
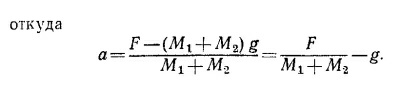
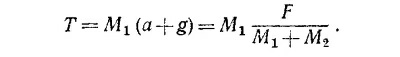
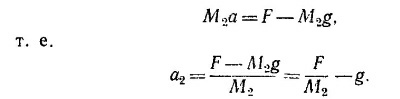
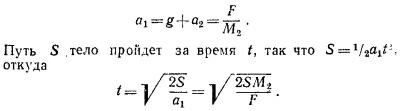
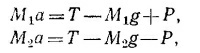
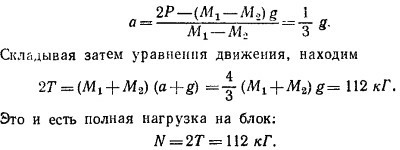
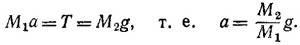
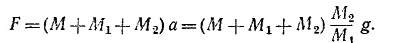
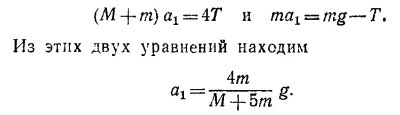
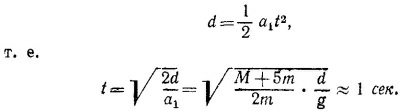
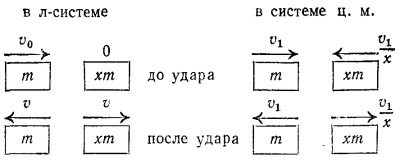
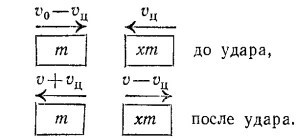
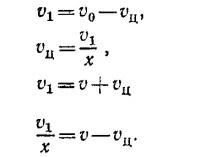
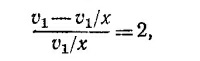
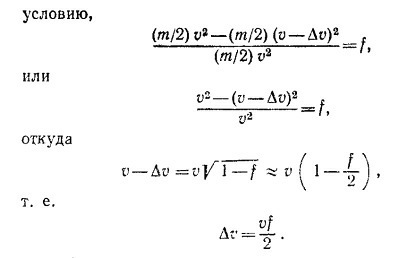
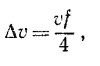
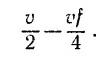
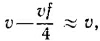
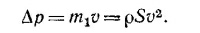
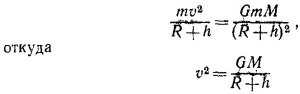
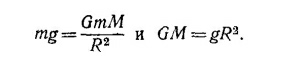
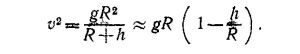
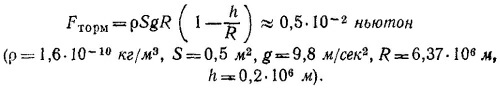
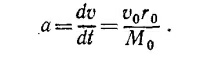
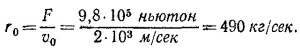
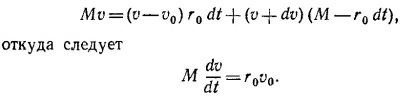
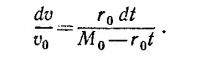
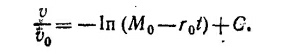
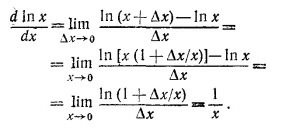
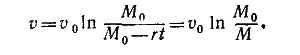
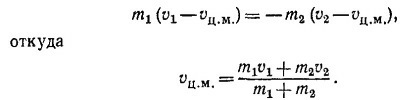
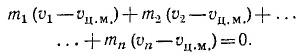
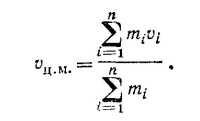
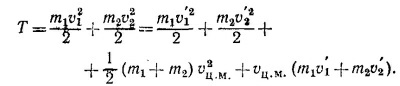
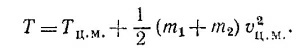
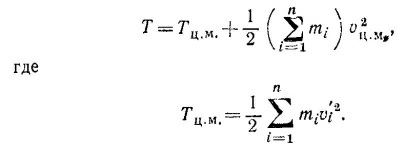

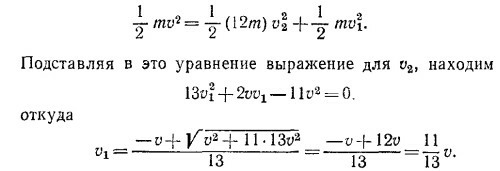
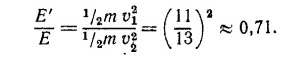
 10.10. Найдем в первую очередь начальную скорость бруска v1. При этом можно воспользоваться законом сохранения импульса: пока брусок не отклонился, горизонтальные силы отсутствуют и поэтому импульс бруска с попавшей в него пулей равен начальному импульсу пули
10.10. Найдем в первую очередь начальную скорость бруска v1. При этом можно воспользоваться законом сохранения импульса: пока брусок не отклонился, горизонтальные силы отсутствуют и поэтому импульс бруска с попавшей в него пулей равен начальному импульсу пули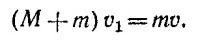
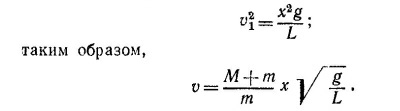
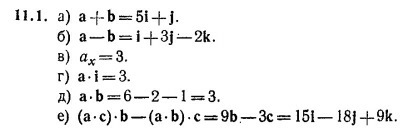
 11.2. а) Велосипедиста обдувают два потока воздуха: встречный, движущийся со скоростью его собственного движения v, и косой— со скоростью v1. Естественно, велосипедист ощущает суммарный результат действия этих двух потоков, так что ему кажется, что ветер дует под углом α. Истинное же направление ветра (к направлению движения велосипедиста) составляет угол φ = α+β. Угол β найдем, принимая во внимание, что v2 = v1-+v, т. е. v1 v2 и v образуют треугольник.
11.2. а) Велосипедиста обдувают два потока воздуха: встречный, движущийся со скоростью его собственного движения v, и косой— со скоростью v1. Естественно, велосипедист ощущает суммарный результат действия этих двух потоков, так что ему кажется, что ветер дует под углом α. Истинное же направление ветра (к направлению движения велосипедиста) составляет угол φ = α+β. Угол β найдем, принимая во внимание, что v2 = v1-+v, т. е. v1 v2 и v образуют треугольник.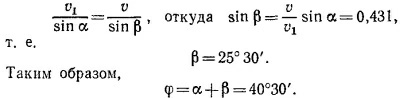
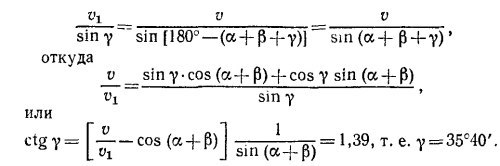
 11.3. а) Выберем систему координат так, чтобы ось х была направлена строго на восток, а ось у—на север. Предположим далее, что второй корабль в начальный момент времени находится в начале координат О, а вектор его скорости v2 образует угол α с осью ОХ. Очевидно, первый корабль находится в точке В, лежащей на оси у на расстоянии 6 миль от О, а его скорость направлена параллельно оси х.
11.3. а) Выберем систему координат так, чтобы ось х была направлена строго на восток, а ось у—на север. Предположим далее, что второй корабль в начальный момент времени находится в начале координат О, а вектор его скорости v2 образует угол α с осью ОХ. Очевидно, первый корабль находится в точке В, лежащей на оси у на расстоянии 6 миль от О, а его скорость направлена параллельно оси х.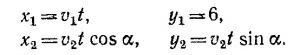
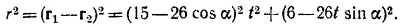
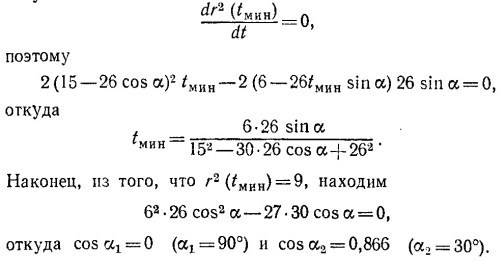
 11.4. Можно считать, что произвольная точка М колеса участвует в двух движениях: равномерном со скоростью v вдоль оси х и вращательном вокруг центра колеса с угловой скоростью ω=v/R (см. задачу 8.12). Пусть в начальный момент времени t = 0 радиус-вектор точки М направлен под углом φ0 к оси х. Действуя точно так же, как и в задаче 8.12, находим координаты х и у точки М в произвольный момент времени t:
11.4. Можно считать, что произвольная точка М колеса участвует в двух движениях: равномерном со скоростью v вдоль оси х и вращательном вокруг центра колеса с угловой скоростью ω=v/R (см. задачу 8.12). Пусть в начальный момент времени t = 0 радиус-вектор точки М направлен под углом φ0 к оси х. Действуя точно так же, как и в задаче 8.12, находим координаты х и у точки М в произвольный момент времени t: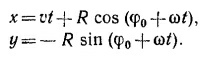
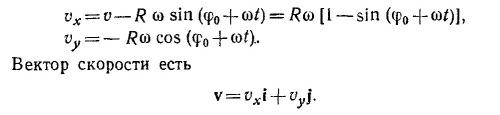
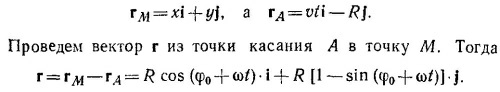
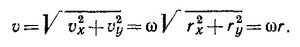
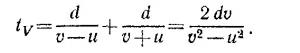
 При движении поперек реки скорость лодки должна быть направлена под некоторым углом α к направлению на противоположный берег (иначе лодка не попадет в нужную точку). Скорость лодки поперек реки равна, как видно из рисунка, √v2—u2 поэтому время движения в поперечном направлении равно
При движении поперек реки скорость лодки должна быть направлена под некоторым углом α к направлению на противоположный берег (иначе лодка не попадет в нужную точку). Скорость лодки поперек реки равна, как видно из рисунка, √v2—u2 поэтому время движения в поперечном направлении равно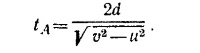
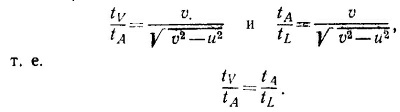
 11.6. Обозначим скорость плывущего человека буквой v, скорость реки через и, а скорость ходьбы человека через v1 Чтобы попасть на противоположный берег в точку В, плывя под некоторым углом к течению, человеку потребуется время (см. предыдущую задачу)
11.6. Обозначим скорость плывущего человека буквой v, скорость реки через и, а скорость ходьбы человека через v1 Чтобы попасть на противоположный берег в точку В, плывя под некоторым углом к течению, человеку потребуется время (см. предыдущую задачу)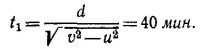
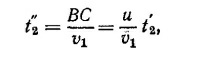
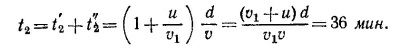
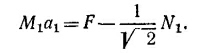
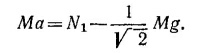
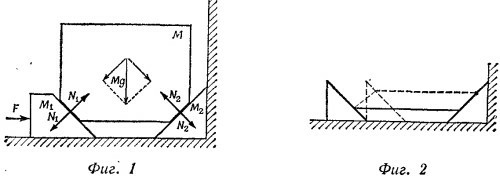
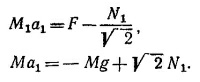
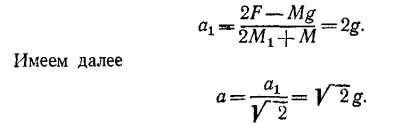
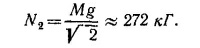
 11.8. Пусть точка М движется по окружности радиусом R с постоянной скоростью v. Время одного оборота, т. е. период движения, есть Т = 2πR/v. К точке М приложены две силы: сила тяжести mg, направленная вертикально вниз, и сила натяжения нити Т, направленная вверх по нити. Очевидно, центростремительная сила Fц= mg+T; она направлена по радиусу горизонтальной окружности. Как видно (см. рисунок), модуль ее равен Fц = mg tg α, где α —угол между нитью и вертикалью, т. е. вызываемое этой силой центростремительное ускорение равно по величине g tg α. С другой стороны, оно, как известно, равно v2/R, поэтому v2/R = g tg α и v2 = gR tg α.
11.8. Пусть точка М движется по окружности радиусом R с постоянной скоростью v. Время одного оборота, т. е. период движения, есть Т = 2πR/v. К точке М приложены две силы: сила тяжести mg, направленная вертикально вниз, и сила натяжения нити Т, направленная вверх по нити. Очевидно, центростремительная сила Fц= mg+T; она направлена по радиусу горизонтальной окружности. Как видно (см. рисунок), модуль ее равен Fц = mg tg α, где α —угол между нитью и вертикалью, т. е. вызываемое этой силой центростремительное ускорение равно по величине g tg α. С другой стороны, оно, как известно, равно v2/R, поэтому v2/R = g tg α и v2 = gR tg α.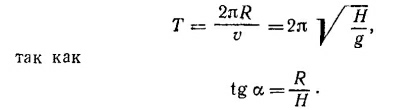
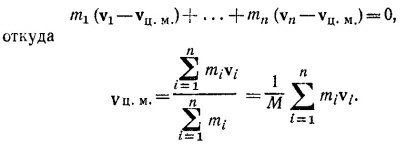
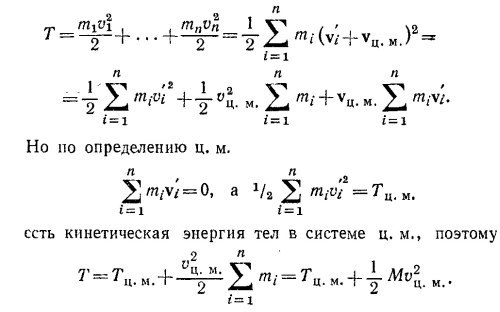
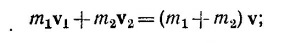
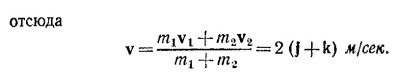
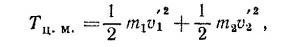
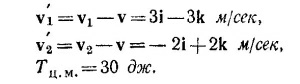
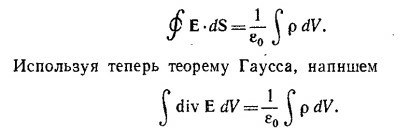
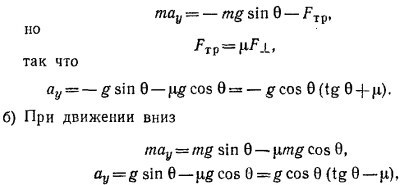
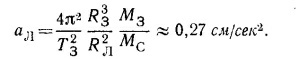
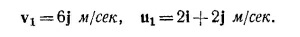
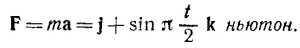

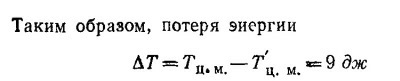
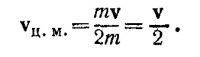
 Начальные скорости частиц в системе ц.м. равны v′1 = v/2 и v′2 = —v/2.
Начальные скорости частиц в системе ц.м. равны v′1 = v/2 и v′2 = —v/2.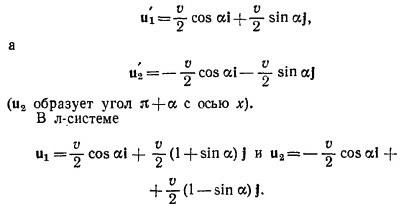
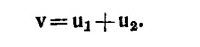

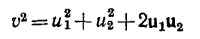
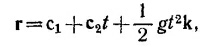
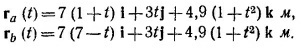
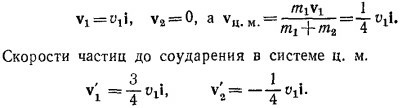
 Так как соударение абсолютно упругое, в системе ц.м. скорости частиц по величине остались прежними, но линия относительного движения повернулась на некоторый угол. Чтобы понять, на какой именно угол повернулась эта линия, рассмотрим отдельно движение второй частицы в л-системе и системе ц.м.
Так как соударение абсолютно упругое, в системе ц.м. скорости частиц по величине остались прежними, но линия относительного движения повернулась на некоторый угол. Чтобы понять, на какой именно угол повернулась эта линия, рассмотрим отдельно движение второй частицы в л-системе и системе ц.м.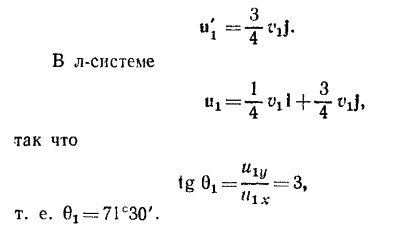
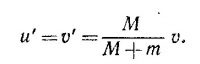
 Направление вектора u′ произвольно, так что конец этого вектора описывает окружность радиусом mv/(M+m) < vц.м.. Поскольку u = u′ +vц.м. , простым геометрическим построением легко найти различные значения вектора u. Как видно из рисунка, угол отклонения налетающей частицы (направление начальной скорости v совпадает с направлением vц.м.) максимален в том случае, когда и направлено по касательной к окружности. При этом
Направление вектора u′ произвольно, так что конец этого вектора описывает окружность радиусом mv/(M+m) < vц.м.. Поскольку u = u′ +vц.м. , простым геометрическим построением легко найти различные значения вектора u. Как видно из рисунка, угол отклонения налетающей частицы (направление начальной скорости v совпадает с направлением vц.м.) максимален в том случае, когда и направлено по касательной к окружности. При этом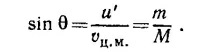
 11.17. Выполнив для частицы массы m такое же построение, как и в предыдущей задаче (только теперь vц.м.=mv/(M+m), a u′m =Mν/(M+m), так что u′m > vц.м.), с учетом того, что угол между vц.м. и um равен 90°, определим u′m = um—vц.м. . Построим теперь на этом же рисунке u′M и uM [u′M = vц.м = mv/(M + m)]. Определим длину BD. Треугольники BDC и АОВ подобны, поэтому
11.17. Выполнив для частицы массы m такое же построение, как и в предыдущей задаче (только теперь vц.м.=mv/(M+m), a u′m =Mν/(M+m), так что u′m > vц.м.), с учетом того, что угол между vц.м. и um равен 90°, определим u′m = um—vц.м. . Построим теперь на этом же рисунке u′M и uM [u′M = vц.м = mv/(M + m)]. Определим длину BD. Треугольники BDC и АОВ подобны, поэтому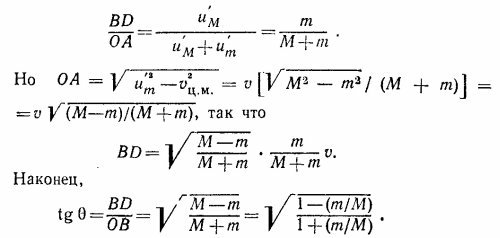
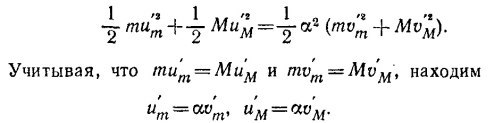
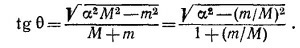
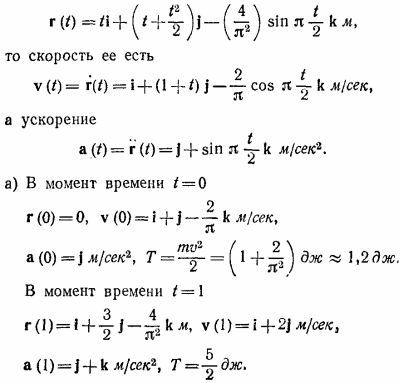
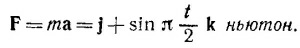
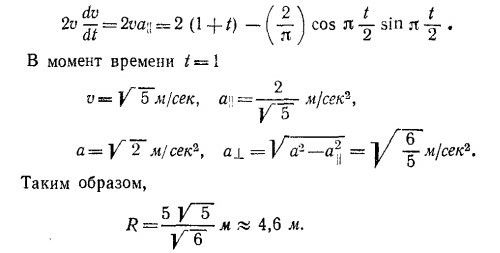
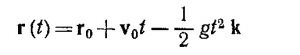
 (ось z направлена вертикально вверх).
(ось z направлена вертикально вверх).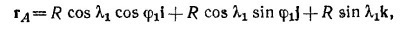
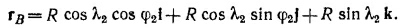
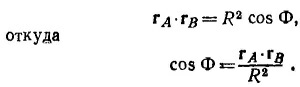
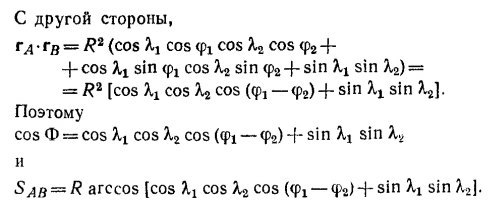
 11.22. На рисунке схематически показано и отмечено цифрами I, II, III положение Луны в новолуние, первую четверть и полнолуние.
11.22. На рисунке схематически показано и отмечено цифрами I, II, III положение Луны в новолуние, первую четверть и полнолуние.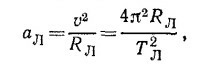
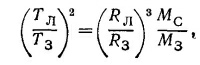
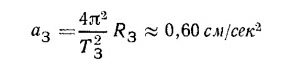

 К главе 12. Характеристики сил
К главе 12. Характеристики сил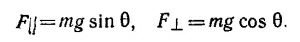
 т. е. если μ≥tg θ, то скользить по наклонной плоскости только под действием силы тяжести кирпич не может.
т. е. если μ≥tg θ, то скользить по наклонной плоскости только под действием силы тяжести кирпич не может.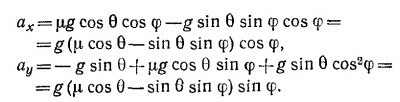
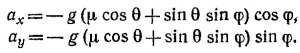
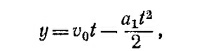
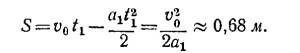
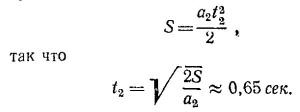
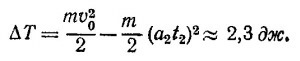
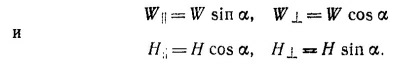
 При достаточно большой силе H груз W начнет двигаться вверх по наклонной плоскости, так как H|| направлено вверх по плоскости, а в отсутствие силы H груз W покоится (μ >tg α). Непосредственно перед началом движения, когда к телу приложена сила Hмин, разность H||мин —W|| должна равняться силе трения. Последнюю получим, умножив силу нормального давления H_мин+ W_ на коэффициент трения μ. Итак,
При достаточно большой силе H груз W начнет двигаться вверх по наклонной плоскости, так как H|| направлено вверх по плоскости, а в отсутствие силы H груз W покоится (μ >tg α). Непосредственно перед началом движения, когда к телу приложена сила Hмин, разность H||мин —W|| должна равняться силе трения. Последнюю получим, умножив силу нормального давления H_мин+ W_ на коэффициент трения μ. Итак,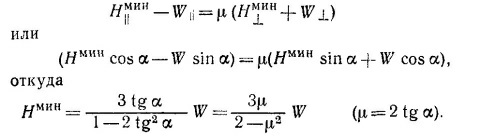
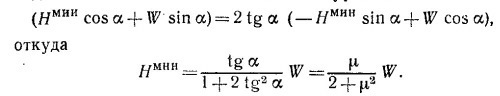
 12.4. В точке О горизонтальная составляющая натяжения нити Т cos α уравновешивается силой трения, которая непосредственно перед началом скольжения кольца равна μТsin α. Таким образом, Т cos α = μТsin α, откуда tgα = 1/μ =4/3.После простых вычислений находим также, что sin α = 4/5. cosα = 3/5. По теореме синусов:
12.4. В точке О горизонтальная составляющая натяжения нити Т cos α уравновешивается силой трения, которая непосредственно перед началом скольжения кольца равна μТsin α. Таким образом, Т cos α = μТsin α, откуда tgα = 1/μ =4/3.После простых вычислений находим также, что sin α = 4/5. cosα = 3/5. По теореме синусов: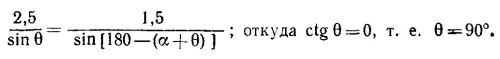
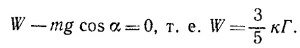
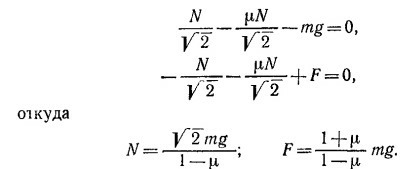
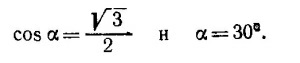
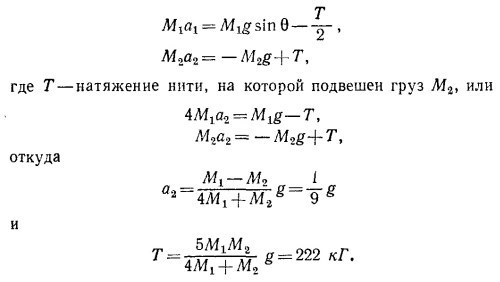
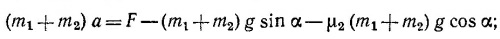
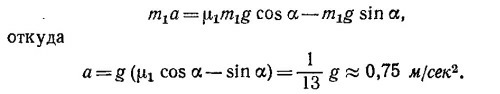
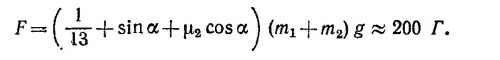
 12.9. Пусть угол θ и коэффициент трения μ таковы, что куб, предоставленный сам себе, начинает скользить. При этом изменение его потенциальной энергии (за счет опускания ц. м.) окажется больше работы силы трения: за счет этой разницы и появляется кинетическая энергия у куба. Ясно, что в положении, когда силы трення едва хватает, чтобы удержать куб, изменение потенциальной энергии при (воображаемом) небольшом смещении куба будет как раз равно работе силы трения. Как видно из рисунка, высота ц. м. куба равна h = (l/√2) cos (45°— θ) (/ —длина ребра куба), а расстояние от нижнего ребра до стенки x = /cosθ.
12.9. Пусть угол θ и коэффициент трения μ таковы, что куб, предоставленный сам себе, начинает скользить. При этом изменение его потенциальной энергии (за счет опускания ц. м.) окажется больше работы силы трения: за счет этой разницы и появляется кинетическая энергия у куба. Ясно, что в положении, когда силы трення едва хватает, чтобы удержать куб, изменение потенциальной энергии при (воображаемом) небольшом смещении куба будет как раз равно работе силы трения. Как видно из рисунка, высота ц. м. куба равна h = (l/√2) cos (45°— θ) (/ —длина ребра куба), а расстояние от нижнего ребра до стенки x = /cosθ.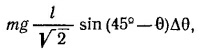
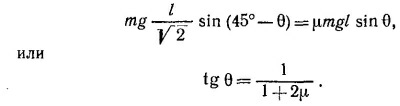
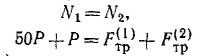
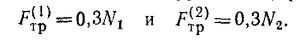

 12.11. а) Если веревка подвинется вправо на расстояние S, то при этом будет выполнена работа ΔTS. Эта работа должна равняться работе сил трення
12.11. а) Если веревка подвинется вправо на расстояние S, то при этом будет выполнена работа ΔTS. Эта работа должна равняться работе сил трення
 12.12. Перейдем в систему координат, жестко связанную с полосой. В этой системе на тело действует псевдосила F=ma. Разложим ее на две составляющие: F|| вдоль полосы и F_ — перпендикулярно к ней. Они равны соответственно (см. рисунок)
12.12. Перейдем в систему координат, жестко связанную с полосой. В этой системе на тело действует псевдосила F=ma. Разложим ее на две составляющие: F|| вдоль полосы и F_ — перпендикулярно к ней. Они равны соответственно (см. рисунок)