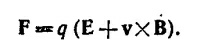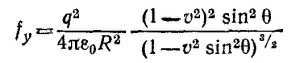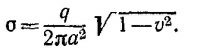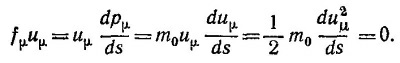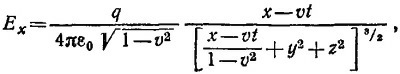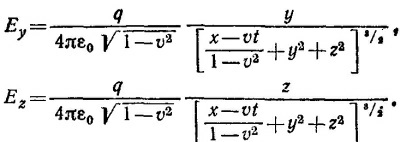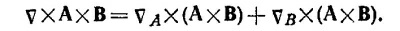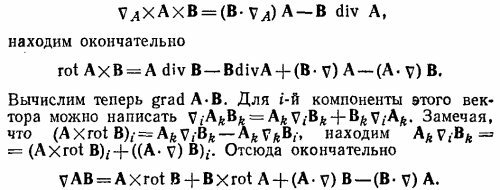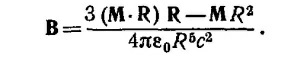| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Решения и ответы
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Следовательно, работа, которую необходимо затратить на преодоление электрического отталкивания при образовании ядра урана U236 из двух одинаковых половинок, приближенно равна (A = 118, Z = 46), EU = 4·10-11 дж = 250 Мэв (2,8·106 квт-час/кг). Для двух ядер дейтерия (A= 2, Z=1), сливающихся в гелий, ЕHe = 7,3·10-14 дж = 0,46 Мэв (5,9· 106 квт-час/кг). Последний результат, однако, гораздо менее точен, поскольку использованное выше выражение для радиуса теряет точность для самых легких ядер.
близка к единице, что оправдывает такое приближение. Уравнение движения частицы
Частица будет совершать все время движение вдоль оси z, §cnw.qEx=qvzB. При этом vx = 0 и vz=const. Следовательно (так как vz=c/3),
1.5. а) Введя обозначение ω = qB0/m, запишем уравнение движения mv=q(vxB) в компонентах vx = ωvy, vy = –ωvx ,vz=0
причем a = v0 (из начального условия vxlt=0 =v0 vylt=0 =0).
окончательно находим, что частица движется по окружности (фиг. 1) в плоскости ху, центр которой находится в точке (0, –v0/ω), частота вращения равна ω=qB/m:
б) В магнитном поле Вх = 0, Bу = 0, Вz = В0 + аx частица полетит по примерно круговой орбите с радиусом r = mv0/qB. Однако в области более сильного поля радиус кривизны траектории будет несколько меньше. При этом орбита уже не будет замкнутой окружностью, а возникнет
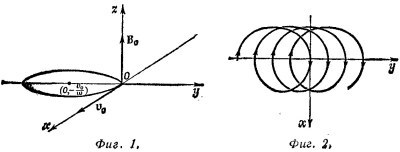
1.6. а) Движение частицы будет происходить по окружности радиусом а вокруг заряда Q, если сила Лоренца будет уравновешена центробежной силой
б) Сила, с которой магнитное поле действует на частицу, всегда перпендикулярна ее скорости. Поэтому магнитное поле не производит работы над движущимся зарядом, и закон сохранения энергии имеет вид
где Е —полная энергия, U(r) — энергия электростатического взаимодействия. Отсюда видно, что скорость частицы есть функция только расстояния
в) В этом случае полная энергия заряда q равна Е = –Qq/4πε0a и, следовательно,
К главе 2. Дифференциальное исчисление векторных полей
Если теперь использовать векторное уравнение потока тепла h =–xvТ и учесть, что векторы h и vT направлены по радиусу цилиндра, то можно написать следующее дифференциальное уравнение:
где D — постоянная интегрирования. Величины J и D определим из условий: температура при r =а равна Т1 а при r = b равна Т2. Отсюда
Следовательно, искомый градиент температуры в изоляционном покрытии равен
б) В этом пункте задачи граничные условия другие, чем в пункте (а), т. е. задано Q —количество тепла, выделяемое током на единице длины медного провода. Если ρ — удельное сопротивление, то, согласно закону Ома,
где / — сила тока, протекающего по проводу. Из этого соотношения находим новое граничное условие
2.2. а) Согласно «Лекциям» [см. вып. 5, § 5, формулы (2.38) — (2,40)], компоненты ротора вектора А равны
Подставляя в это выражение компоненты ротора А и учитывая тот факт, что порядок вычисления смешанных производных произволен, т. е. что, например, д2Ах/дzду= д2Ах/дудz, легко убеждаемся в равенстве нулю дивергенции ротора произвольного вектора А.
Согласно определению, левая часть этого соотношения может быть записана в виде
Прибавляя и вычитая в правой части последнего соотношения величину д2Ах/дхг и учитывая, что дАх/дх + дАу/ду+дАz/дz= v · А, убеждаемся в справедливости соотношения (1). Аналогично доказывается это соотношение для компонент у и z.
в) Легко убедиться, что если φ — произвольная скалярная функция, а А —произвольный вектор, то всегда
Это соотношение полезно запомнить. Из него, в частности, следует и требуемое в условии соотношение. Действительно, выбирая в качестве φ=1/R3 и A = R, а также учитывая, что, согласно пункту (a), v·R = 3 и vφ=–3R/R5,
Вычисление градиента скалярной функции, зависящей только от модуля радиуса-вектора,—довольно часто встречаемая операция. Поэтому полезно запомнить легко доказываемое соотношение
г) Искомое соотношение можно доказать вычислением «в лоб». Однако в силу того, что вычисление ротора—одна из популярных операций в физике, полезно доказать гораздо более общее cоотношение
В том, что оно справедливо, можно убедиться непосредственной проверкой. Искомое соотношение следует из вышеприведенного лишь как частный случай. Действительно, выбирая φ = –1//R3 и A=R, учитывая (1) и тот факт, что RxR = 0 и vXR=0 [см. пункт (б) настоящей задачи], находим
в) Результат этого пункта задачи следует как частный случай из соотношения (1).
С другой стороны, согласно уравнению l,div E=ρ/ε0. Отсюда видно, что из уравнения 4 действительно следует уравнение 5.
Если теперь использовать уравнение 1, то получим искомое волновое уравнение.
Из этого уравнения мы видим, что ротор вектора Е+(∂A/∂t)=0 тождественно обращается в нуль. Это означает, что весь этот вектор может быть представлен как градиент скалярной функции φ (скалярный потенциал электромагнитного поля), так как ротор градиента произвольной скалярной функции φ тождественно обращается в нуль
В выполнении последнего соотношения легко убедиться непосредственным вычислением. Но и без этих вычислении ясно, что векторное произведение вектора v на самого себя, каковым и является правая часть этого соотношения, всегда равно нулю.
где ω—вектор угловой скорости.
Если теперь использовать соотношение (б) задачи 2.3, то получим требуемый результат.
2.6. При операциях с вектором v следует всегда помнить, что он действует на векторы, стоящие после него. Поэтому в данном случае формулой для двойного векторного произведения можно пользоваться, но следует изменить в последней формуле порядок сомножителей, т. е. вместо (v·A)R поставить (A·v) R. К главе 3. Интегральное исчисление векторов
Так как это равенство выполняется для произвольной замкнутой поверхности, то, следовательно, div E = ρ/ε0. Второй закон электромагнетизма гласит: циркуляция вектора Е по любому контуру равна производной по времени от потока вектора В сквозь произвольную поверхность, опирающуюся на этот контур, т. е.
Используя теорему Стокса, запишем
Так как, согласно третьему закону электромагнетизма, поток вектора В через любую замкнутую поверхность равен 0, то ф B·dS = ∫ div В dV = 0. Отсюда div B=0.
б) Выберем произвольный объем и проинтегрируем по этому объему левую и правую части уравнения Δj = — ∂ρ/∂t:
Если воспользоваться теперь теоремой Гаусса, то это уравнение можно представить в виде
Левая часть этого соотношения представляет собой скорость изменения заряда внутри объема, а правая — количество заряда, вытекающего (втекающего) в единицу времени из объема. Следовательно, равенство этих частей выражает закон сохранения заряда: сколько зарядов убыло в объеме, столько их и вытекло из этого объема.
Так как токи и электрическое поле, создаваемое растущим со временем зарядом шара, радиальны, то написанные выше потоки векторов j и Е через поверхность S составляют лишь долю от потока этих векторов через замкнутую сферическую поверхность, равную S/4πR2. Но, согласно закону Гаусса и закону сохранения заряда,
Величина q(t) в этом соотношении обозначает заряд шара в момент времени t. Следовательно,
Так как контур был выбран произвольным, то мы делаем вывод, что касательная к сфере составляющая вектора В равна нулю. Равенство нулю радиальной составляющей вектора В следует из того, что поток вектора В через поверхность сферы должен быть равен нулю, и из того, что в силу сферической симметрии системы Вr одинакова во всех точках сферы.
К главе 4. Электростатика
4.2. Найдем потенциал φ в точке Р, расположенной на оси диска на расстоянии r от его центра, разбив диск на кольца шириной dρ и средним радиусом ρ. Так как отдельные элементы каждого такого кольца одинаково удалены от точки Р на расстояние √ρ2+r2. то все они дадут одинаковый вклад в φ. Интегрируя по кольцам, т. е. по ρ от 0 до R, находим
(где Ω— телесный угол, под которым виден диск из точки Р) и направлена вдоль оси диска.
г) При r>rс в выражении для потенциала появляется слагаемое, спадающее с расстоянием быстрее, чем 1/r, т. е. как 1/r2. Оно описывает отличие поля от сферически симметричного.
Итак, средние значения потенциала по сферическим поверхностям разных радиусрв равны между собой. Вместе с тем среднее по поверхности, близкой к началу координат, равно φ(0). Итак,
5.2. Используя цилиндрическую симметрию задачи, по теореме Гаусса найдем
где Q —полный заряд цилиндра, R —его радиус, L — его длина. Следовательно, напряженность электрического поля цилиндра линейно зависит от расстояния до оси цилиндра. В случае шара радиусом R электрическое поле радиально и зависит от r аналогичным образом
5.3. Потенциалы пластин по условию задачи равны. Отсюда
При этом использован тот факт, что поле выше и ниже пленки однородно. Окружая пленку соответствующей поверхностью, легко найти по теореме Гаусса, что E + E′ = ε/ε0, где σ —плотность поверхностных зарядов на пленке. Отсюда находим
5.4. Рассмотрим бесконечно тонкий слой, заключенный между двумя параллельными плоскостями, перпендикулярными оси х и расположенными друг от друга на расстоянии dx. Из условия задачи ясно, что электрическое поле будет направлено вдоль оси х. Если в качестве гауссовой поверхности выбрать любой цилиндрик, основаниями которого являются площадки S на плоскостях, а его боковая поверхность перпендикулярна этим плоскостям, то, применяя теорему Гаусса, найдем
Разлагая в ряд левую часть этого равенства и оставляя лишь наибольшие члены, находим уравнение для Е (х):
5.5. В силу симметрии задачи φ (х, у, z)= φ(х).
(это уравнение Максвелла v·E = ρ/ε0 в одномерном случае). Отсюда, используя результат пункта (а) данной задачи, находим
5.7. Так как напряженность электрического поля вблизи поверхности проводника связана с плотностью поверхностных зарядов σ = еоE, то число избыточных зарядов (электронов) равно
Расстояние между атомами—порядка ангстрема (1Å= 10-10м). Поэтому число атомов на единицу площади равно приблизительно 1020м-2. Отсюда Δn/n ~ 3·10-5. Сила, испытываемая электроном в поле протона, равна
Сравним силы F1 и F2 = qeE. Принимая величину а (боровский радиус) равной примерно 1Å, находим
5.8. Если рассматривать ядро как равномерно заряженный шар, то электрическое поле внутри ядра легко найти по теореме Гаусса:
Здесь R—радиус ядра, Q—полный заряд ядра. Уравнение движения мюона с массой μ (нерелятивистское) имеет вид
Найденная оценка позволяет интерпретировать наблюдаемое явление как переходы между уровнями энергии осциллятора с испусканием γ-лучей соответствующей энергии.
где γ —гравитационная постоянная, a R и М — радиус и масса Земли. Уравнение движения тела
Для спутника, вращающегося над самой поверхностью Земли, равенство центробежной силы и силы гравитации
что и требовалось показать.
где D —постоянная интегрирования, которую следует найти из граничного условия. В качестве последнего можно выбрать Т (R) =0. Удовлетворяя граничному условию, находим D=Q/8πxR и, следовательно,
Отсюда температура в центре Земли T(0)=Q/8πxR=50 000°K. Таким образом, описанная модель не находится в согласии с оценками.
Из найденных выражений следует:
Абсолютные величины сил равны
6.2. Сила притяжения к электростатическому изображению равна
(потенциал на бесконечности принят равным нулю). Кинетическая энергия заряда на расстоянии х от поверхности равна разности потенциалов
При x→0 Т→∞. Это нефизично. На самом деле плоскость на бесконечно малых расстояниях нельзя рассматривать как идеально гладкую проводящую плоскость. Оценка при х = 1Å, x0 = 1 см приводит к величине
6.3. Обозначим длину, ширину и толщину бруска через 2а, 2b и 2с соответственно. Пусть r —расстояние от центра бруска вдоль интересующей нас прямой. Для r»а потенциал φ, создаваемый бруском, такой же, как и для точечного заряда
Приближенно можно считать эту формулу справедливой вплоть до r = а. При меньших r (b < r < а) разумную аппроксимацию φ дает потенциал длинной нити, который запишем в виде
Постоянную D выберем из условия непрерывности потенциала при r = а. Находим D = 4ρbс/2πε0.
При с < r < b хорошее приближение дает формула для бесконечной плоскости
6.4. Заряд, накопившийся на Земле за время t, равен q=ηSqpt, где η = 1 протон /см2 ·сек — плотность потока частиц, S= 4πR2—площадь поверхности Земли, R —радиус Земли, qр—заряд протона. Критический заряд q Земли, при котором все заряды с кинетической энергией E< 4·109 эв не будут попадать на Землю, находится из очевидного условия
Земля, по оценкам, существует 5·109 лет; казалось бы, на Землю уже давно не должно падать ни одного протона. На самом же деле, положительный заряд Земли постоянно компенсируется за счет потока электронов, энергия которых настолько мала, что эти электроны не относят к космическим лучам.
где q—заряд на единицу длины, φ1—φ2 —разность потенциалов цилиндров конденсатора. Поскольку из соображений симметрии поле Е внутри конденсатора радиально, то по теореме Гаусса находим
Если на поверхности внутреннего цнлиндра будут острые выступы, емкость конденсатора уменьшится, так как напряженность поля вблизи выступов будет велика, а расстояние между цилиндрами почти не изменится. Это приведет к увеличению разности потенциалов между обкладками и, следовательно, к уменьшению емкости. 6.6. а) Чтобы найти поле системы точечный заряд—проводящая сфера, надо поступить следующим образом (см. «Лекции», вып. 5, стр. 125). Необходимо поместить изображение заряда q величины q′= — (a/b)q на радиусе, проходящем через заряд q на расстоянии а2/b от центра сферы, и, кроме того, в центре сферы поместить заряд q″= — q′ (см. рисунок).
б) Решим теперь задачу о точечном заряде вблизи проводящей сферы, потенциал которой равен V. Выражение для потенциала в этом случае имеет приведенный выше вид, но с той лишь разницей, что заряд q″ в центре сферы следует заменить на Va4πε0. Таким образом,
При этом сила, действующая между сферой с заданным потенциалом и зарядом, равна F=F·b/b, где
Для нашего случая вектор Е в некоторой точке Р, находящейся внутри сферы, равен
Расписывая это соотношение в компонентах и принимая во внимание, что x1 = x2 y1= y2, z1 = z2 —d, находим
Радиальная составляющая напряженности электрического поля равна
Тангенциальная составляющая Eθ определяется градиентом в перпендикулярном к радиусу-вектору направлении. Приращение расстояния на этом пути равно dl = rdθ (см. рисунок), поэтому
Так как потенциал не зависит от угла φ, Eφ = 0.
т. е. не зависит от расстояния до диполя.
6.9. а) Потенциал в пространстве при наличии однородного электрического поля равен
Если радиус сферы равен а, то р = E0а3·4πε0.
е) Полученные результаты могут быть использованы, в частности, для решения задачи о поле и распределении зарядов металлической сферы, помещенной в однородное внешнее электрическое поле.
где i и j —единичные векторы в плоскости, перпендикулярной нити, направленные вдоль осей х и у соответственно. Найдем выражения для силы F и момента силы М, действующих на диполь в произвольном электрическом поле с напряженностью Е (r). Предположим, что отрицательный Заряд диполя находится в точке с радиусом-вектором r, а положительный заряд в точке с радиусом-вектором r+d, так что дипольный момент диполя равен p = qd. Тогда суммарная сила, действующая на диполь, может быть представлена как сумма сил, действующих на его заряды
Считая величину d малой, разложим электрическое поле в точке r + d в ряд по d и ограничимся линейными по d членами разложения:
Чтобы вычислить момент этой силы, действующей на диполь, поступим аналогичным образом. Вспоминая определение момента силы, с точностью до линейных по d членов находим
Учитывая найденное выше выражение для силы F, окончательно находим М=рхЕ (r)+rXF.
В случае (б) момент силы направлен перпендикулярно плоскости, проходящей через нить и диполь.
в) Пусть х»а. Тогда с точностью до членов порядка а2/х2
Следовательно, электрическое поле кольца убывает быстрее поля диполя. Это происходит в силу того, что дипольный момент заряженного кольца равен нулю.
б) Значение потенциала в начале координат можно найти из интегрального выражения
в котором интегрирование производится по объему палочки. Интегрирование удобно выполнить в так называемой цилиндрической системе координат. Именно, разбивая поперечное сечение цилиндра на кольца площадью 2πrdr, а длину цилиндра на отрезки dx, представим
Так как l/2r≥50, разложим подынтегральную функцию в ряд по степеням отношения 2r/l. Ограничиваясь первыми двумя членами разложения, найдем
Точность этого выражения оценим, вычислив поправку aR6/6ε0l2. Подставляя численные значения из условия задачи, найдем φ (0, 0, 0) ≈ 2350 в, причем ошибка примерно составляет 0,15 в.
Эквипотенциальные поверхности определяются условием r2/r1=const, т. е.
Если это уравнение записать иначе, т. е. (х— а)2+у2 = R2, то видно, что оно описывает цилиндр вращения.
К главе 8. Электростатическая энергия
Из этой энергии следует вычесть «нефизическую» энергию самодействия протонов. Энергия, соответствующая протону, заряд которой равномерно размазан по шару радиуса r, равна U2 = 3/5 (q2/r) (1/4πε0). Для Z протонов эта энергия «действия самого на себя» равна 3Zq2/5r·4πε0. Следовательно, электростатическая энергия кулоновского взаимодействия протонов в ядре равна 3/5Z (Z—1) (q2/4πεor).
8.3. Суммарная энергия конденсаторов до их параллельного соединения равна
Поскольку при параллельном соединении конденсаторов их емкости складываются, то энергия системы после соединения равна
Избыток энергии излучается или теряется на тепло в соединительных проводах. Потери энергии не происходит, если q1C2 =q2C1.
б) Вычислим момент силы, действующей на диполь, прямым вычислением. Полный момент внешних сил равен Разлагая это выражение в ряд с точностью до членов первого порядка по | r1,2| «| R |, находим
Отсюда в случае однородного электрического поля следует М = рХЕ. Последнее выражение получается также из выражения (1): если ввести угол α между векторами р и Е, то действующий на диполь момент будет равен по величине
и направлен перпендикулярно плоскости, в которой лежат векторы р и Е, т. е. M = рХЕ.
Таким образом, энергия диполя в этом случае будет меньше и равна
Искомая разность энергий равна q3/4πε0|р| и имеет смысл энергии взаимодействия зарядов, составляющих диполь.
а работа этой силы на расстоянии dх равна —(q2/2ε0A) dx.
Из условия Δ= W получается радиус пиона а = 2·10–14 см. Отсюда видно, что так определенный радиус пиона оказывается меньше характерных размеров ядра.
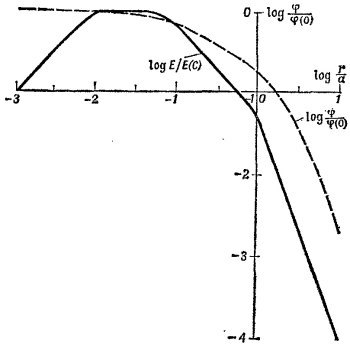
Когда оболочка имеет заряд q2 ситуация несколько иная. В начальном состоянии, когда заряд q1 находится на бесконечности, энергия, сосредоточенная в поле, равна энергии точечного заряда q1 плюс энергия, заключенная в поле, создаваемом сферической оболочкой. Последнее, как легко убедиться на основании теоремы Гаусса, отлично от нуля лишь при r ≥ b и совпадает с полем точечного заряда величины q2. В конечном же состоянии, когда заряд q1 находится в начале координат, величина напряженности электрического поля в пространстве ведет себя следующим образом (разумеется, поле всюду радиально):
К главе 10. Диэлектрики
где V —разность потенциалов на обкладках, а интегрирование производится по двум областям конденсатора. Поскольку поле Е в конденоаторе можно считать однородным, то из этого соотношения, если принять во внимание, что Ed=V, следует
10.2. Емкость конденсатора без диэлектрика равна Со = Aε0/d, где А — площадь пластин, d —расстояние между ними; Q = C0V0, где V0—разность потенциалов. При вдвижении диэлектрика величина Q не меняется, емкость же возрастает и равна (см. решение к задаче 10.1, учтя, что x1 = 1) С = Aε0(1+х)/2d = С0 (l1+x)/2. Энергия конденсатора при этом равна U = Q2/2C =C0V02/(1 +x).
в) Меньше.
10.4. Вектор электрической индукции D в любой точке r внутри диэлектрика равен
Поверхностная плотность зарядов σпол равна σпол = Рn. Следовательно, наведенные на внутренней и внешней поверхностях диэлектрика заряды Qa и Qb, соответственно равны
10.5. Изменение внутренней энергии конденсатора U, равной, как известно, U =Q2/2C (где Q —заряд на пластинах, С — емкость), в процессе, в котором механические силы вдвигают диэлектрик, изменяя его емкость, а батарея совершает работу по изменению зарядов на величину dQ, равно
Первое слагаемое в этом выражении —работа, совершенная электрической батареей по изменению заряда на пластинах конденсатора, а второе —работа механических сил.
а) Подсчитаем работу, совершенную электрической батареей. Учитывая, что заряд на пластинах в начальном состоянии равен q0, а в конечном состоянии xq0, находим
б) Емкость конденсатора в начальном состоянии была q0/V0, а в конечном состоянии xq0/V0. Следовательно, механические силы совершили работу
Работа, как мы видим, совершалась над диэлектриком.
где С1 и С2 —емкости трубки до и после втягивания масла на высоту h. Так как емкость единицы длины цилиндрического конденсатора равна С0«=2πε0/ ln (b/а) (см. решение к задаче 6.5), то
Вес столба втянутого масла равен π (b2—a2)ρgh. Потенциальная энергия этого столба в поле силы тяжести равна весу, умноженному на координату его центра тяжести, т. е. на h/2:
Из равенства работы механических сил потенциальной энергии находим требуемый результат:
Отсюда следует искомое граничное условие
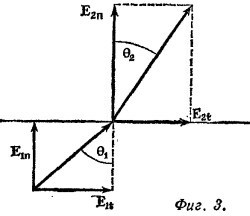
Но при стремлении dl к нулю вклад в интеграл по контуру от боковых сторон будет также стремиться к нулю. Если длину L верхней и нижней сторон рамки выбрать достаточно малой, напряженность электрического поля Е на этих сторонах рамки можно считать однородной. Отсюда (E1t)L–(E2t)L = 0, или E1t = E2t. Из фиг. 3 видно, что
К главе 11. Внутреннее устройство диэлектриков
Здесь, очевидно, вектор Р совпадает с вектором полного дипольного момента равномерно поляризованного шара. Внутри же такого шара поле Е, согласно решению к задаче 6.7, равно
11.2. Дипольный момент атома гелия равен
11.3. Для водяного пара [см. «Лекции», вып. 5. уравнение (11.21)] х— 1 = Np02/3ε0kT. Следовательно, температурная зависимость поляризуемости α =x —1/N имеет вид α= A/T, где A =p02/3ε0k; N—число частиц в единице объема можно найти из уравнения состояния идеального газа p = NkT (р—давление пара, k—постоянная Больцмана). По данным таблицы, приведенной в условии задачи, N= 1,138·1025 м-3. Для α получается следующая таблица значений:
Если построить зависимость α = f(1/T), то экспериментальные точки ложатся на прямую, тангенс угла наклона которой равен А = 1,12. Отсюда ро= √ЗεоkA = 2·10–17 кулон·м.
Поскольку дипольные моменты атома кислорода и атома титана равны рO =αOε0E и pTi = αTiε0E, то при подстановке в эти выражения Е следует искомое условие:
11.5. В однородном внешнем электрическом поле Е каждый шарик будет равномерно поляризован. Пусть Р —вектор поляризации шара. Равномерная поляризация шара создает внутри него однородное электрическое поле с напряженностью, равной —Р/Зε0 [см. «Лекции», вып. 5, формула (11.24)]. Тогда суммарное электрическое поле внутри каждого шарика (их взаимным влиянием друг на друга мы, согласно условию задачи, пренебрегаем) равно Е¡ = Е—Р/Зε0. Поскольку Р = ε0(х—1) Е¡, то
Получим полный дипольный момент равномерно поляризованного шарика P, умножив Р на объем шара, т. е. на (4π/3) (d/2)3:
Поскольку шарики образуют пространственную решетку с периодом, равным 3d, поляризация этой решетки, т. е. дипольный момент, приходящийся на единицу объема решетки, будет равен
Так как D = E + P/ε0, то для диэлектрической постоянной решетки находим выражение
К главе 12. Электростатические аналогии
где Q —полный заряд кольца Q = ρπa2b. Переходя к задаче о распределении температуры, надо вспомнить, что мы вычислили разность потенциалов между центром кольца и бесконечно удаленной точкой. Если потенциал на бесконечности равен φ0, то в центре кольца он равен
Переходя к «температурным» величинам, находим температуру в центре кольца (при таком переходе φ→ Т, ρ →ε0S/x, см. «Лекции», вып. 5, стр. 234, 235)
12.2. Используя аналогию с электростатической задачей, находим Т (r) = — (Sr2/6x) + D, где S = W/(4π/3) R3—плотность источников тепла; W=8·1020 дж/год; R —радиус Земли. Константу D определим из условия Т(а)=Т0, т. е. D = T0+Sa2/6x. Радиус а можно найти, положив приближенно температуру поверхности Земли равной нулю. Из этого условия следует
12.3. а) Трехмерный случай:
Подставляя это выражение для φ в уравнение Δφ = 0, получаем
Нетривиальное решение получившегося уравнения будет при условии, что коэффициенты b1 и b_2 отличны от нуля. Следовательно,
б) Двумерный случай:
В этом случае Δφ=n∑ (n — 1) (n+ 1)сnzρn–3 = 0. Следовательно, лишь c1 и c-1от нуля и решение имеет вид
12.4. Задача математически аналогична задаче 7.1. Поэтому для Т можно сразу написать решение, если в задаче 7.1 линейную плотность зарядов положить равной λ=Wε0/xt
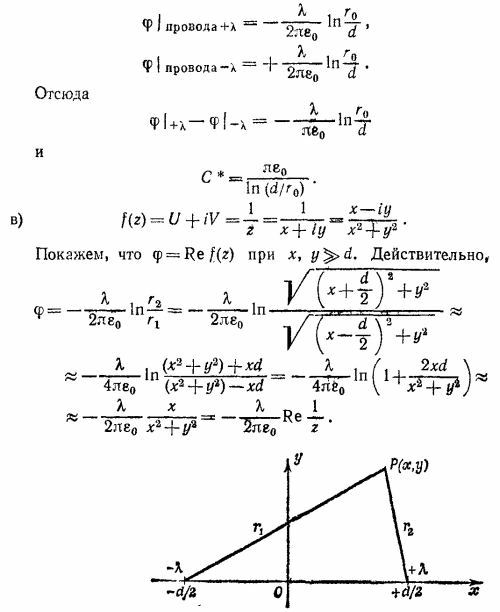
В этом выражении r2=√[x—(d/2)]`2+ y2 и r1 = √[x+(d/2)]`2+ y2—расстояния до произвольной точки от труб с +W и —W источником (см. рисунок к решению задачи 7.1, стр. 421). Постоянная D = T0 определяется из того условия, что вдали от труб температура равна Т0. В точке с координатами х= 100 d и у=100 d температура равна Т = 20,5° С.
Направление вектора В совпадает с направлением вектора угловой скорости.
13.4. Под действием силы Лоренца qev X B электрон будет двигаться по окружности. Радиус последней находится из уравнения движения электрона в магнитном поле: его ускорение равно центростремительному
где v0 — начальная скорость электрона. В своем движении электрон в узкой части трубки опишет дугу. Отклонение луча (в предельном случае на половину экрана) найдем из выражения D/2 = (/ — a) tg φмакс (обозначения расшифрованы на рисунке). Так как а«l, то tg φмакс = D/2I. Нетрудно убедиться, что если отказаться от условия а«l, то φмакс надо определять из уравнения
Сила, действующая на провод, равна найденной по величине, но противоположно направлена,
где еz — единичный вектор в направлении оси z. Интегрируя соотношение Еz = — ∂φ/∂z, находим электрический потенциал φ = –(σ/2ε0) z (постоянную интегрирования выбираем равной нулю). Используя сформулированное выше правило, находим
Так как В = v х А, то, проделав необходимое дифференцирование, находим Вх = 0, By = σv/2ε0c2, Вz = 0. В векторной форме
14.2. Для решения задачи удобно воспользоваться законом Био —Савара
а) Прямолинейные участки провода вносят в величину магнитного поля в центре полукруга нулевой вклад.
в) Слагаемое ~х2 обращается в нуль при условии 5b2/4 = r02 т. е. если а = b.
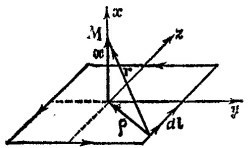
14.4. а) Выберем оси координат, как показано на рисунке. Согласно закону Био—Савара
Ясно, что первый интеграл в квадратной скобке равен нулю просто в силу симметрии рамки, поскольку для любого dl всегда найдется на рамке другой участок, расположенный на таком же расстоянии r от точки М, но с противоположным направлением dl. Что же касается второго интеграла, то в нем вектор dl x ρ всегда направлен вдоль оси х, и, следовательно, магнитное поле рамки перпендикулярно плоскости рамки. Из рисунка видно, что (dl x ρ)x = (а/2) dz.
Вычисляя этот интеграл, получим требуемый в задаче ответ.
По соображениям, изложенным выше, векторный потенциал в точке М равен нулю. Вычислим В = vхА. Воспользовавшись примечанием к задаче, запишем выражение для векторного потенциала в произвольной точке наблюдения
В последнем интеграле дифференцирование производится по координатам точки наблюдения. При этом дифференцировании вектор dl следует считать постоянным. Здесь удобно воспользоваться теми соотношениями, которые были получены в решении к задаче 2.3. Получим
Следовательно, мы приходим к закону Био—Савара, использованному в пункте (а).
Так как токов в направлении оси z нет, то Az=0. Учитывая далее, что
Вычисляя напряженность магнитного поля В = v хА, находим окончательно Вх = Ву = 0:
14.6. Полный заряд проводящей сферы связан с потенциалом V соотношением Q = 4nε0Va. Поэтому плотность поверхностных зарядов равна ε = ε0V/a. Для определения векторного потенциала воспользуемся общим интегральным представлением, учтя, однако, что возникающие при вращении сферы токи будут поверхностными и, следовательно, в условиях задачи надо заменить jdV на (σaωXdS), где dS — вектор, по величине равный элементарной площадке dS и направленный перпендикулярно этой площадке. Векторный потенциал при этом равен
Преобразуя поверхностный интеграл в объемный по теореме Гаусса, найдем
где вектор Е0 — напряженность поля равномерно заряженного шара
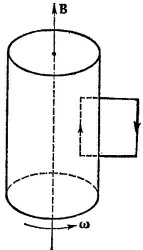
14.7. а) Если отрезком проволоки соединить ось цилиндра с его поверхностью, то, поскольку провод движется в магнитном поле, сила q (v X В) приведет к тому, что концы провода зарядятся. Зарядка будет происходить до тех пор, Пока электрическое поле Е не уравновесит (v X В), т. е. при Е (х) = ω·х·В. При этом разность потенциалов на концах провода будет равна V=0∫b E (x) dx=(ωb2/2) В, где b —радиус цилиндра. Магнитное поле внутри цилиндра (вне его оно равно нулю) легко найти с помощью теоремы Стокса, выбирая контур интегрирования так, как показано на рисунке: В = λω/2πεе0с2. Отсюда ответ:
Для определения равновесных углов θ вычислим «механическую» энергию диполя в магнитном поле, создаваемом сверхпроводником
Определяя равновесные значения θ из условия ∂U/∂θ = 0, найдем θ = 0, π/2, Зπ/2, π. Для найденных значений углов энергия магнитного диполя равна
Следовательно, при θ = 0,π равновесие будет устойчивым, а при θ= π/2, Зπ/2 —неустойчивым,
При устойчивом равновесии, т. е. при θ = 0,π, F = 3μ2/8d4. Сила будет отталкивать диполь от поверхности сверхпроводника.
Мгновенное ускорение следует определить из уравнения движения: mw = qe [E + v x H]. Так как в начальный момент времени скорость заряда равна нулю, то w = (qe/m)Et = —(qеr/2m) (∂Bl∂t). Ускорения в точках P1 и Р3 по величине равны qea(∂Bl∂t)/2m= 1,32·1020 см/сек2 и противоположны по направлению. Ускорение в точке Р2 равно нулю.
17.3. При R»a поле, создаваемое витком (/), равно
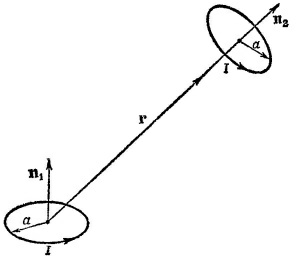
где μ=Iπa2n1; n1 —единичный вектор нормали к плоскости витка (/). Если ввести n2 —аналогичный вектор для витка (2), то магнитный поток через второй виток равен
Так как n1||R, то, введя угол α, который вектор n2 образует в момент времени t с векторами n1 и R, найдем наведенную в витке (2) э. д. с.
Так как провод движется равномерно, то действующая на него сила (сила Ампера) равна нулю. Отсюда / = 0 и, следовательно, vстац = EId· В.
где I1, /2 —токи в катушках; M —коэффициент взаимной индукции. Поскольку по условию задачи /1 = /2 = /, то электрическую энергию цепи можно представить в виде U = 1/2Ll2, где L = L1 + L2—2M. Если витки одной катушки перемотать в другую сторону, то изменится знак у M.
Приравнивая это выражение величине 1/2LI2, найдем индуктивность, приходящуюся на единицу длины кабеля:
б) В этом случае напряженность магнитного поля В при а< r <b равна найденной в пункте (а). С помощью теоремы Стокса найдем, что для 0 < r < а В = Ir/2πε0с2а2. Вычислим далее энергию магнитного поля во внутреннем проводе, приходящуюся на единицу длины. Поступая так же, как в пункте (а), получаем
Складывая это выражение с U1 и приравнивая сумму величине 1/2LI2, находим
Если b»а, то из найденного выражения для L следует, что результат слабо зависит от характера распределения тока по сечению центрального провода.
где N —число витков обмотки, I —сила тока в обмотке. Далее вычислим энергию магнитного поля внутри тороидальной катушки. Интегрируя по объему тороида, найдем
где /1 — сила тока в проводе. Поскольку в катушке N витков, поток нужно умножить на N. Следовательно, э. д. с. в катушке дается выражением
в) Из пунктов (а) и (б) следует, что L/|M|=N.
где µ1 = Iπа2n1. Так как вблизи витка 2 поле В можно считать однородным, магнитный поток через него вектора В равен πа2В·n2. Вычисляя э.д.с, наведенную в витке 2, находим
Через углы α1 и α2 (см. рисунок к условию задачи, стр. 356) взаимная индукция выражается следующим образом:
б) Сила взаимодействия витков [см. «Лекции», вып. 6, формула (17.39)] равна F=— I2vM12. Используя выражение (1), находим
Составляющая силы, перпендикулярная плоскости рисунка, равна нулю. Проекции силы F на линию, соединяющую центры витков, F|| и на перпендикулярную к ней ось (на рисунке направим эту ось вверх) F_ соответственно равны
17.9. Чтобы найти напряженность магнитного поля на оси соленоида, создаваемого одним витком, определим вначале вектор В0 на оси. Воспользовавшись результатом задачи 14.5, найдем, что на расстоянии z от центра витка напряженность магнитного поля на его оси равна по величине
При этом вектор Во направлен вдоль оси витка. Чтобы найти напряженность магнитного поля в центре соленоида, создаваемого всеми его витками, проинтегрируем найденное выражение по длине соленоида, введя линейную плотность тока IN/l. Заменяя в приведенном выше выражении для В0 силу тока на INdz/l и интегрируя по z от —l/2 до +l/2, находим величину магнитного поля в центре соленоида:
Нетрудно видеть, что, если длина соленоида стремится к бесконечности, выражение для В переходит в найденное в «Лекциях» (вып. 5, гл.13, §5) выражение для магнитного поля внутри длинного соленоида. В силу того что r2»r1 поле В в окрестности петли можно считать однородным (т.е. в области 0< r < r1). Вычисляя магнитный поток через петлю Ф = В·πr12, находим
Вычислим теперь M21. Так как размеры витка малы, то его можно рассматривать как магнитный диполь. Поле магнитного диполя равно (см. «Лекции», вып. 6)
где µ = I1πr12ez; еz —единичный вектор, направленный по оси соленоида (ее выбираем в качеств оси z); /1 —сила тока в витке. Вычислим поток вектора В через один виток соленоида, расположенный на расстоянии z от центра витка:
Если сила тока в витке меняется, то в рассматриваемом витке соленоида наводится э.д.с, равная E =— ∂Ф/∂t. Чтобы найти полную э.д.с, мы должны просуммировать найденное нами выражение по всем виткам. Вводя плотность витков Ndz/l и интегрируя по z от –l/2 до l/2, находим
Вычисляя найденный интеграл, получаем выражение для M21, которое, как нетрудно видеть, совпадает с M12 т.е. M21=M12
Отсюда I = E/R=–Bvl/R=–10–8а. Если не пренебрегать магнитным полем, создаваемым движущимся проводником, ток в цепи уменьшится. Ответ по величине не изменится, если магнит, создающий поле В, будет двигаться со скоростью v в ту же сторону, что и провод, так как в этом случае можно считать, что сопротивление R движется вправо со скоростью v и, следовательно, магнитный поток через цепь будет меняться с прежней скоростью. Так как размеры цепи уменьшаются со временем, коэффициент самоиндукции также будет уменьшаться.
Где d —расстояние между центрами витков; α —угол, который составляет нормаль к витку Б с осью, проходящей через эти центры; MАБ—коэффициент взаимной индукции витков, Чтобы найти последний, можно воспользоваться результатом задачи 17.8 (см. формулу для M12);
Витки отталкиваются друг от друга.
Для компоненты α(α = x, у, z) это уравнение имеет вид
Подставляя в это уравнение Eα = E0αexp [i (ωt—kx)] и выполняя дифференцирование, находим [k2 —(ω2/с2)]Eα =0. Так как ω=ck, это уравнение выполняется для любого α.
Выбранная точка, таким образом, движется в положительном направлении оси х со скоростью c.
в) Подействуем оператором v на функцию
Следовательно, действие оператора v на подобные функции сводится к простому умножению их на вектор —ikex. Действие оператора ∂/∂t сводится к умножению таких функций на число ¡ω.
Определяя Е из последнего уравнения и подставляя выражение для Е во второе уравнение, находим
так как exX(exX B)= ex(ex·B)–B(ex·ex). Учитывая, что, согласно третьему из полученных уравнений, exB=0, а также что (ex·ex)=1, из (1) находим [k2—(ω2/с2)] В=0. Отсюда следует, что ω = ck.
Этот результат совпадает с тем, который можно получить, используя преобразования Лоренца.
что эквивалентно выражению (21.26) «Лекций», вып. 6, стр. 155.
где t′= t—r′±/c. Напряженность электрического поля, создаваемая зарядами +q и —q в точке Р, согласно уравнению (21.1) (см. «Лекции», вып. 6, стр. 142), равна
Воспользуемся тем, что точка Р находится на расстоянии r»d от диполя. Это позволяет во всех вычислениях ограничиваться лишь линейными по d членами. В таком приближении
Учитывая, что ez·eθ=cos θ, находим, что эти скалярные произведения равны нулю. Модули векторов der±/dt и d2er±/dt2 найдем, вычислив скалярные произведения этих векторов на eθ. Учитывая, что (ez·eθ) =—sin θ, имеем
Определяя из этого выражения Еφ, Еθ, и Еr, приходим к приведенному в условии задачи результату.
Это происходит от того, как отмечалось в «Лекциях», что дипольные поля возникают, когда мы находимся далеко от всех токов и зарядов. Тогда в большой части пространства уравнения для Е и В одинаковы: ротор и дивергенция этих полей равны нулю. Но нетрудно убедиться, что подобная симметрия уравнений Максвелла имеет место и в общем случае переменных полей. Действительно, в далеких от зарядов и токов точках пространства уравнения Максвелла однородны:
Поэтому, заменяя в выражениях для электрического и магнитного полей осциллирующего диполя, найденных в задаче 21.2,
21.4. а) Из рисунка к условию задачи (стр. 361) видно, что (для удобства обозначим d/2=a)
получаем требуемое выражение для φ.
Если воспользоваться уравнением vA=—(1/с2) (∂φ/∂t), которое в задаче сводится к уравнению (1/с2) (∂φ/∂t) =— (∂Аz/∂z), то мы видим, что в написанном выше выражении для (1/с2) (∂φ/∂t) функция, стоящая после оператора ∂/∂z, есть не что иное, как — Az. Если воспользоваться уравнением vA=—(1/с2) (∂φ/∂t), которое в задаче сводится к уравнению (1/с2) (∂φ/∂t) =— (∂Аz/∂z), то мы видим, что в написанном выше выражении для (1/с2) (∂φ/∂t) функция, стоящая после оператора ∂/∂z, есть не что иное, как — Az.
Умножая Е скалярно на er,eφ=ezX er и еθ=еr X(ezX er) = cosθer—ez, находим выражения для Eφ, Eθ, Er, приведенные в условии задачи 21.2. При этом сВ=еrх Е.
Дипольный момент элементарного диполя длиной Δz отсюда равен
где k = 2π/λ, и подставляя в формулу для векторного потенциала, простым интегрированием находим Аz:
Нетрудно видеть, что последнее выражение совпадает с найденным векторным потенциалом А в пункте (б) задачи 21.4, если только положить
Поэтому мы можем воспользоваться решением к этой задаче [см. пункт (в) задачи 21.4] и найти электрическое поле в волновой зоне
Аналогично для магнитного поля находим, что в волновой зоне существенна лишь компонента Вφ , причем она равна Вφ=Eθ/c.
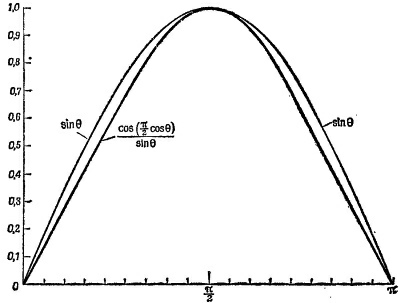
Характер этой зависимости для антенны и одного диполя примерно одинаковый (см. рисунок).
21.6. Электрическое и магнитное поля движущегося заряда описываются потенциалами Льенара-Вихерта
где R′ и v′ берутся для времени t′ = t — R′/c.
где v′ [t′]=v[t — (а/с)]. Считая момент времени, когда заряд находится в точке Р, за начало отсчета времени, находим
Наша конечная цель —вычислить производные от потенциалов в начале координат. Поэтому, выражая R′ как функцию t, х, у, удержим лишь члены первого порядка по r
Выразим теперь через х, у, t скалярное произведение (v′·R′). Как видно из рисунка, (v′·R′)=—va sinα1. Имеем
Если подставить сюда только что найденное выражение для R′, мы найдем cosα1 = 1, однако если учесть члены второго порядка, то в конце концов получим
Воспользовавшись формулой Е = — vφ— (∂A/∂t), вычислим напряженность электрического поля [напомним, что вектор А в центре круга найден в пункте (б)]. Имеем
Легко убедиться, что при t=0, т. е. когда заряд находится в точке Р, Еx < 0 и Еу < 0. Таким образом, поле направлено вниз от оси х (а если бы был справедлив «запаздывающий закон Кулона», оно было бы направлено выше оси х).
Отбрасывая в выражении для Ах члены, пропорциональные х, а в Ау—пропорциональные у (и те и другие не дают вклада в магнитное поле), находим
Нетрудно убедиться, что только z-компонента магнитного поля отлична от нуля. Для нее
Таким образом, магнитное поле в центре круга не зависит от времени. Оно равно полю в центре витка с током, таким, что ∫ I·dS = qv.
г) Формула (21.1) для напряженности электрического поля (см. «Лекции», вып. 6, гл. 21, стр. 143) принимает в нашем случае вид
Дифференцируя, получаем для Ех и Еу формулы, совпадающие с уже найденными. Вычислим магнитное поле
что опять совпадает с прежним результатом.
Сопротивление при таком подсоединении равно 5/6 ом.
При данном подсоединении сопротивление схемы равно 7/12 ом.
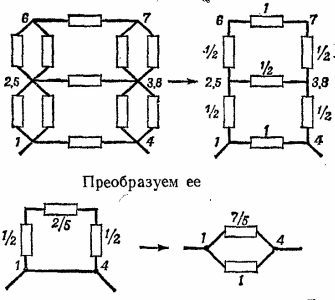
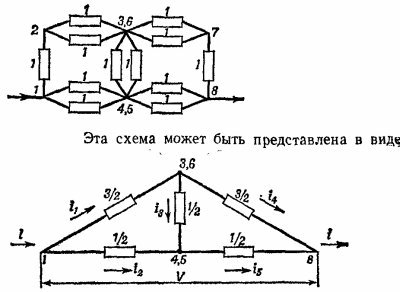
Сопротивление такой цепи (см. «Лекции», вып. 6, стр. 180) нельзя вычислить, пользуясь лишь формулами для параллельных и последовательных сопротивлений. Чтобы Найти ее сопротивление, запишем уравнение Кирхгофа для токов и напряжений (см. схему):
Решая эту систему уравнений, находим i1 =i4=i/4, i2=i5=Зi/4 , i3 = 0. Отсюда для напряжения V между узлами 1 и 8 получаем
т.е. сопротивление цепи равно 3/4 ом. Другие возможные подсоединения сводятся к одному из рассмотренных выше.
Если теперь ввести комплексную э.д.с. V = V0е¡ωt , то комплексный ток равен
Определяя вещественную часть этого выражения, находим силу тока в цепи
б) В этом случае каждая из индуктивностей станет равной L+M и ответ будет таким, как был найден выше, но L перейдет в L+ M, а С в С/(1+ω2MС). Действительно, если обозначить через iC и iL токи через параллельно соединенные емкость и индуктивность L, так что iC +iL = I где I — полный ток в цепи, то
С другой стороны, согласно закону Кирхгофа, для напряжений имеем
Из последнего уравнения видно, что уравнения такие же, как и в пункте (а), но
Учитывая это, находим комплексный ток в цепи
Вещественная часть этого выражения дает нам искомую силу тока в цепи
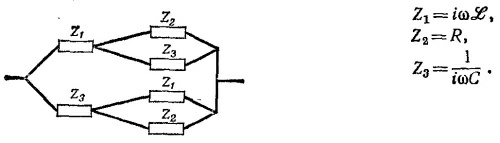
22.3. а) Схему можно представить в следующем виде:
Импеданс верхней цепи при этом равен
а импеданс нижней Z″ = z/(Z1 + Z2), где Z = Z1Z2 + Z1Z3 + Z2Z3. Полный импеданс цепи равен Z = Z′Z″/(Z′ +Z″) = Z/(Z1+2Z2 + Z3). Подставляя в последнее выражение Z¡, с учетом того что R2= L/2C, получаем Z = R.
Качественно зависимость фазы от частоты изображена на рисунке.
22.5. При параллельном соединении импеданс цепи находится следующим образом: Z–1 = R–1 + i [ωC—(1/ωL)]. Вводя комплексную э. д. с. V = Voexp (iωt) и определяя силу тока в цепи I = V/Z (ω), находим выражение для амплитуды силы тока
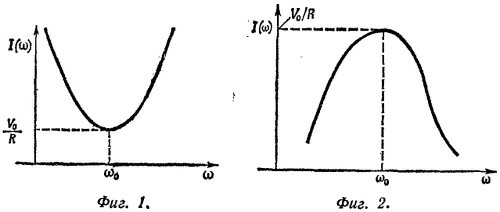
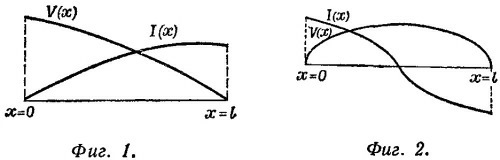
При ω02 = 1/LC наступает «резонанс»: при этом условии сила тока в цепи минимальна и равна (по амплитуде) /мин = V0/R. Примерный характер «резонансной» кривой изображен на фиг. 1. При малых ω ток в цепи течет в основном через индуктивность, а при больших —через емкость. В момент резонанса ток течет лишь через активное сопротивление.
где ω02=1/LС. Если 1/RС«ω0, т. е. R» √L/C, эту формулу можно упростить (таким же образом, как и в гл. 23)
Ширину резонансной кривой определим по частотам, при которых I02 в два раза больше, чем в резонансе. Находим Δω=1/RC. При последовательном соединении элементов импеданс цепи Z (ω) = R +¡ [ωL—(1/ωС)], а амплитуда тока
Резонансная кривая в этом случае имеет вид, изображенный на фиг. 2. Зависимость I02 от частоты здесь равна
Ширина резонансной кривой равна Δω = R/L. Если R= k√L/C для параллельного соединения и R=1/k√L/C для последовательного, то ширина резонансной кривой в обоих случаях в k раз меньше резонансной частоты.
Из этих выражений следует, что R2 = RaRb и, следовательно, L = CR2.
Приравнивая по отдельности вещественные и мнимые части этого уравнения, находим условия баланса:
22.8. Импеданс цепи легко находится:
а) Пусть RC = L/R. Тогда Z = R. Следовательно, амплитуда тока в этом случае не зависит от частоты.
где Z1 = R/?/(1 + ¡ωСR).
22.9. Суммарная емкость m одинаковых последовательно соединенных конденсаторов равна Собщ=С/m. Импеданс цепи Z равен сумме сопротивлений: емкостного Zc=—im/ωC, индуктивного Z1= iωL и активного сопротивления, равного R. Если э.д.с. представить в комплексной форме, то из закона Ома следует
Вещественную часть силы тока можно представить в виде
Мощность, выделяемая на активном сопротивлении, максимальна при m, удовлетворяющем условию ωL– (m/ωC) ≈0, т. е. при m≈ ω2СL.
К глаее 23. Полые резонаторы
где I —полный ток, который течет через конденсатор. Имеем В =I/2πε0с2r. Определим W=1/2LI2 — энергию магнитного поля в тороидальной части полости:
Отсюда находим L = [(b—а)/2πε0с2] In (b/а) и, следовательно, получаем искомое выражение для резонансной частоты
Так как при охлаждении полости все ее размеры d,а,b уменьшатся в одинаковое число раз, резонансная частота не изменится.
Эта энергия равна 1/2L0I2, следовательно, индуктивность единицы длины L0 =а/ε0с2b. Емкость плоского конденсатора равна C = ε0A/d, где А — площадь пластин конденсатора, а d —расстояние между ними. Таким образом, емкость, приходящаяся на единицу длины линии, равна C0 = ε0b/a. Отсюда импеданс линии равен
24.3. Направим ось z вдоль оси цилиндра. Величина напряженности электрического поля в рассматриваемом случае зависит только от z и r (r —расстояние от оси цилиндра). Зависимость от z необходима для того, чтобы поле на торцах секции, где оно параллельно проводящей поверхности, обращалось в нуль, а зависимость от r при фиксированном z можно найти, используя теорему Гаусса. Имеем E = f(z)/r, где f(z) — некоторая подлежащая определению функция z. Компоненты напряженности электрического поля равны Ex=(x/r2)f(z), Ey=(y/r2) f (z). Для каждой из этих компонент справедливо уравнение
которое после подстановки в него выражения для Ех сводится к
Решением такого уравнения являются синусы и косинусы. Нам нужно такое решение, которое обращается в нуль при z = 0 и z =l. Очевидно, таким решением будет sin (πnz/l), где n —целое число. Стало быть ω = πnc/l. Для самой низкой моды n = 1 и ω= πc/l.
24.5. а) Напряжение в произвольной точке х в момент времени t есть суперпозиция падающей и отраженной волн:
г) Так как поглощение отсутствует, средняя работа, производимая генератором, равна нулю [в этом можно убедиться также, вычислив среднее значение I(0) V0 (0)]. Поэтому и средний момент силы равен нулю.
Мы имеем два уравнения для А1 и А2, поэтому находим эти величины, а затем силу тока при x = 0
а) Если ZT = 0, то Zs = ¡Z0 tg ωl√LC; Zs=0 при ωl√LC=πn, Zs=∞ при ωl√LC =π/2 + πn.
24.7. На стыке двух передающих линий выполняются следующие условия «сшивки»:
решая которую, получаем искомый ответ.
Магнитное поле действительно поперечно, так как Bz = 0 (волна распространяется вдоль оси z). Легко убедиться, что найденное поле В удовлетворяет волновому уравнению ΔВ — (1/с2) (∂2В/∂t2) = 0. Проверим теперь выполнение граничных условий. Внутри идеального проводника, из которого, как мы считаем, сделаны стенки волновода, переменное магнитное поле должно отсутствовать (иначе возникли бы бесконечно большие индукционные токи). Так как силовые линии магнитного поля имеют вид замкнутых петель, то на стенках волновода должны быть отличны от нуля лишь тангенциальные составляющие вектора В. Но это так и есть на самом деле, поскольку Bz=0
Электрическое поле также удовлетворяет волновому уравнению ΔЕ — (1/с2) (∂2Е/∂t2)=0. Согласно граничным условиям, на стенках волновода должны быть равны нулю касательные составляющие, т. е. должно быть Еу = 0 при х = 0 и х = а, Ех = 0 при у = 0 и у = b и Ez = 0 на стенках волновода. Найденные выражения для компонент напряженности электрического поля удовлетворяют этим условиям.
(В релятивистских обозначениях это можно написать как ∑налет.част.Pμ= ∑разлет.част.Pμ.) Из треугольника ОАВ находим m2v2 =h2v02+h2v2—2h2v0v cosφ, а из закона сохранения энергии следует m = h (v0—v) + m0. Возводя обе части этого соотношения в квадрат и вычитая из получившегося уравнения ранее найденное из треугольника ОАВ соотношение, несложными преобразованиями находим
где φ —угол отклонения направления распространения фотона от первоначального.
Порог реакции будет соответствовать нулевым скоростям электронов и позитрона v1 = v3 = v2 = 0. Отсюда 2Еγминmе + mе2 = 9mе2. Следовательно, Еγмин = 4mе = 2,04 Мэв.
Отсюда находим массу покоя новой частицы:
В нерелятивистском случае, т. е. при v2«1, m1 = m+М. Скорость новой частицы в лабораторной системе координат связана с импульсом р′ и энергией Ε′ частицы соотношением: V = р′/Ε′. Согласно закону сохранения импульса,p = р′, а согласно закону сохранения энергии, Ε′= m+ √p2+M2.Отсюда
В нерелятивистском случае (v2 «1) получаем известный результат
К главе 26. Лоренцевы преобразования полей
Выразим в этих уравнениях Е′ и В′ через Е и В в системе К с помощью лоренцевых преобразований (см. соответствующие формулы преобразования в табл. 26.2 «Лекции», вып. 6, стр. 273).
Поскольку система К выбрана так, что Еx = 0 и Вx=0, два последних уравнения удовлетворяются автоматически, из первого уравнения следует, что
26.5. Рассмотрим систему координат К′, в которой заряд покоится. В этой системе координат В′ = 0, Е′ = qR′/4πε0R′3. Используя формулы преобразования для компонент векторов Е и В при лоренцевых преобразованиях, находим, что в лабораторной системе К (см. табл. 26.2; в формулах этой таблицы нужно Только заменить v на –v):
где R′2=[(x-vt)2+(y2+z2)(1—v2)]/(1—v2) (согласно лоренцевым преобразованиям x′= (x—vt)/√1-v2, у′=y, z′ = z). Подставляя выражение для R′ в выражения для компонент векторов E и В и вводя обозначение
Если ввести θ —угол между векторами rр {х—vt, у, z} и v, то R*2 = r2р (1—v2sin2θ). Поэтому векторы Е и В можно представить в виде
26.6. См. решение к задаче 26.5.
где I —вектор силы тока [по поводу этой формулы см., например, «Лекции», .вып. 5, стр. 263, формула (13.18)]. Если ось х направить вдоль вектора I, то r = √y2 +z2 и
б) Чтобы найти поля Е и В в системе координат К′, движущейся вместе с электронами, необходимо воспользоваться формулами преобразования полей при лоренцевых преобразованиях (см. табл. 26.2, вып. 6, стр. 273). В результате найдем
В рассматриваемой лабораторной системе координат В = 0 и, следовательно, F = (σq/2ε0) ey. Заряды отталкивают друг йруга с силой Кулона
(см. решение к задаче 26.5), где θ —угол между векторами v и R — радиусом-вектором,соединяющим два заряда. По условию задачи θ = π/2. Поэтому fy = (q2/4πεоа2) √1—v2. Движущиеся заряды не будут отклоняться от плоскости, если Fy = fy. Отсюда следует ответ
Поскольку при малых скоростях зарядов σ≈σ0= q2/2πа2, то отношение плотностей зарядов на поверхности плоскости при релятивистских скоростях к плотности зарядов в нерелятивистском случае равно σ/σ0=√1—v2. Так как энергия частицы со скоростью v2 равна Е = m/√1—v2, то σ=σ0(m/Е). Поскольку по условию задачи энергия заряда равна 500 Мэв, то, учитывая, что m = 0,5 Мэв, находим σ/σ0 = 10-3.
26.10. а) Прежде всего нужно определить «запаздывающее положение» частицы, т. е. выяснить, на каком этапе движения создается интересующее нас поле. Для этого достаточно ответить на вопрос, какое время больше — затраченное светом для того, чтобы пройти из начала координат в точку (а,а), или затраченное частицей для того, чтобы достичь точки (а, 0), выйдя опять-таки из начала координат. Так как v/c = 0,5, второе время больше, т. е. поле создается зарядом во время его равномерного движения вдоль оси х.
Согласно условию задачи z = 0, y = a, x=а, vt1=a, v = 1/2. Отсюда Ex = Ez = 0, Ey=q/2√3πε0а2.
Индексы A и В у v мы приписали для удобства, чтобы яснее отметить тот факт, что при дифференцировании оператор v действует только на соответствующий вектор, а другой вектор при этом считается постоянным. Далее, замечая, что
27.2. Напряженность магнитного поля диполя с магнитным моментом M равна
Выберем сферическую систему координат, начало которой совпадает с центром Земли, а ось z — с направлением вектора М. Величину М можно определить через магнитное поле у поверхности Земли на экваторе В0 = M/R034πε0с2, где R0 - радиус Земли. Считая Землю шаром, вычислим энергию внешнего по отношению к Земле магнитного поля по формуле W = (εoc2/2) ∫ B2dV. Подставляя в эту формулу выражение для В, легко несложным интегрированием показать, что W=4πε0с2B02R03/3≈103 Мгm. Отсюда ясно, что по энергетическим соображениям взрыв водородной бомбы в 1 Мгт не может существенно исказить магнитное поле Земли.
Продолжение. Решения и ответы к задачам V-VII томов фейнмановских лекций по физике СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

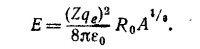
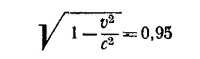
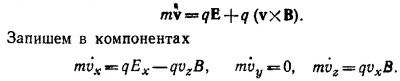
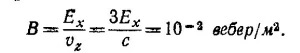
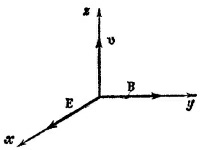 Заряд частицы не входит в последнее выражение. Поэтому его знак из данного эксперимента установить невозможно.
Заряд частицы не входит в последнее выражение. Поэтому его знак из данного эксперимента установить невозможно.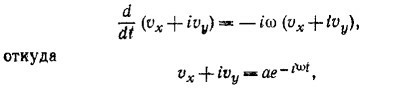
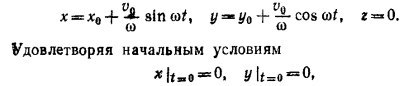
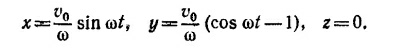
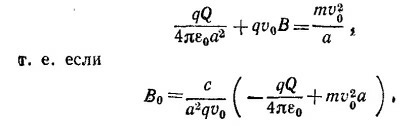
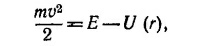
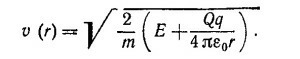
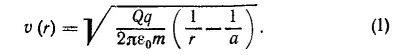
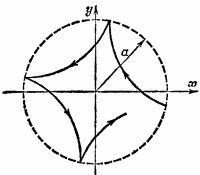 Начав в начальный момент «падать» на заряд —Q, частица q будет отклонена полем так, как показано на рисунке. Из выражения (1) видно, что в точках окружности r= а скорость частицы будет обращаться в нуль и будет вновь повторяться исходная ситуация.
Начав в начальный момент «падать» на заряд —Q, частица q будет отклонена полем так, как показано на рисунке. Из выражения (1) видно, что в точках окружности r= а скорость частицы будет обращаться в нуль и будет вновь повторяться исходная ситуация.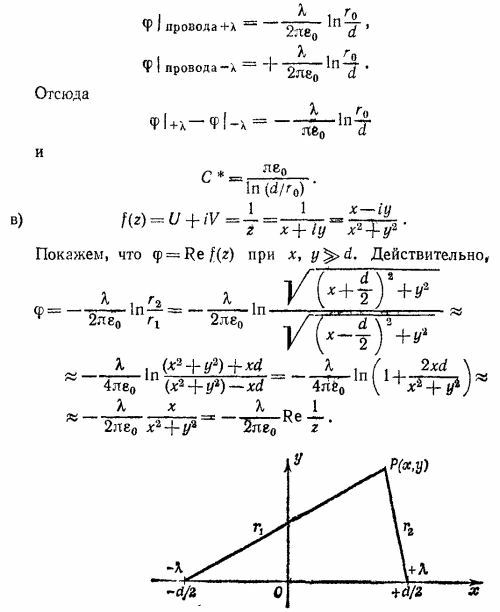
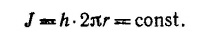
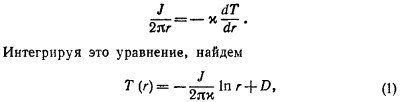
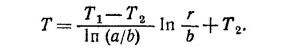
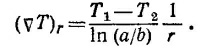
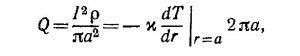
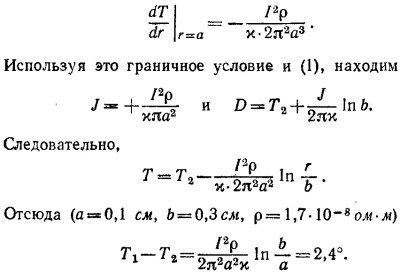
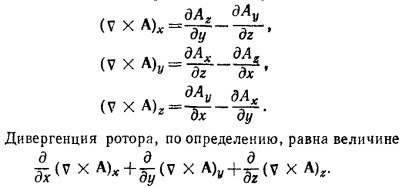
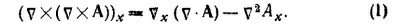
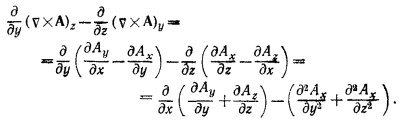
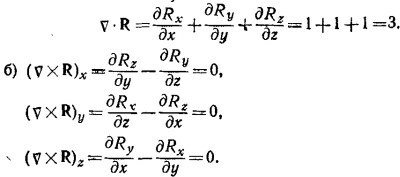
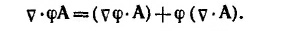
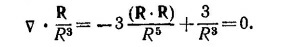

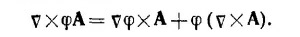
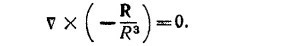
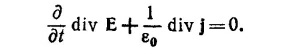
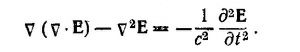
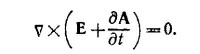
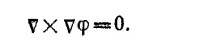
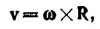

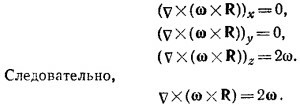
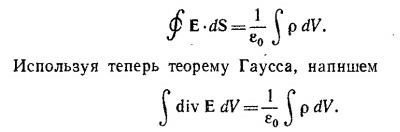
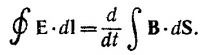
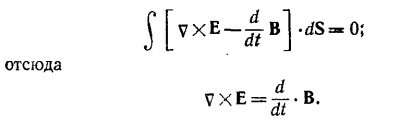
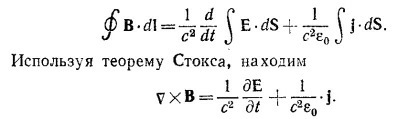
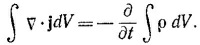
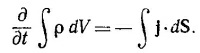
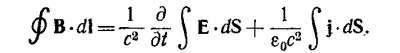
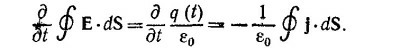
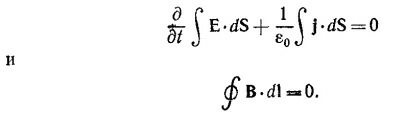
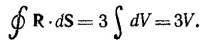
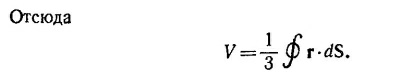

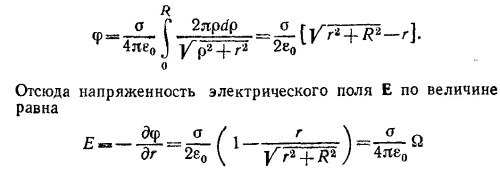
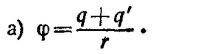
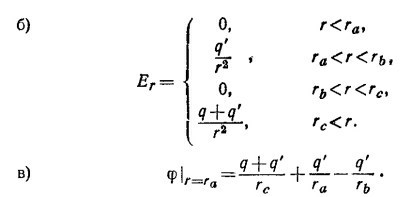
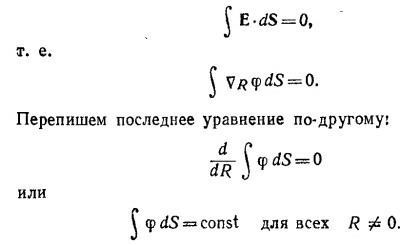
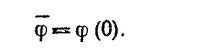
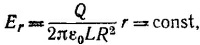
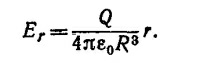
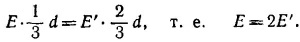

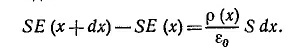
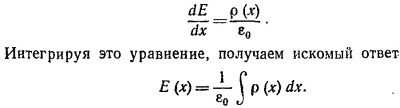
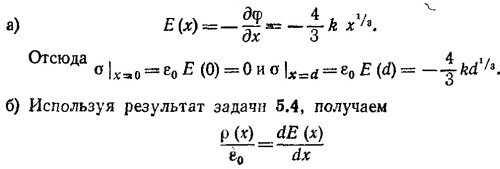
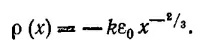
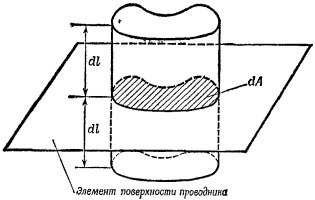 5.6. В задаче надо различать поле Е, созданное самим элементом площади, и поле, созданное всеми остальными элементарными площадками на поверхности проводника. Окружим элемент поверхности dA гауссовой поверхностью в форме цилиндра, боковые поверхности которого перпендикулярны площадке dA. Тогда, согласно теореме Гаусса, поле Е, созданное элементарным зарядом σdA внутри проводника, равно σ/2ε0. Поскольку, однако, поле внутри проводника равно нулю, то, следовательно, остальные поверхностные заряды создают в объеме (охватываемом гауссовой поверхностью) поле, равное σ/2ε0, но противоположно направленное. (В результате сложения получается, что электрическое поле внутри равно нулю, а вне—равно σ/ε0.) Отсюда следует, что полная сила, действующая на выделенный элементарный участок площади со стороны всех остальных зарядов, равна
5.6. В задаче надо различать поле Е, созданное самим элементом площади, и поле, созданное всеми остальными элементарными площадками на поверхности проводника. Окружим элемент поверхности dA гауссовой поверхностью в форме цилиндра, боковые поверхности которого перпендикулярны площадке dA. Тогда, согласно теореме Гаусса, поле Е, созданное элементарным зарядом σdA внутри проводника, равно σ/2ε0. Поскольку, однако, поле внутри проводника равно нулю, то, следовательно, остальные поверхностные заряды создают в объеме (охватываемом гауссовой поверхностью) поле, равное σ/2ε0, но противоположно направленное. (В результате сложения получается, что электрическое поле внутри равно нулю, а вне—равно σ/ε0.) Отсюда следует, что полная сила, действующая на выделенный элементарный участок площади со стороны всех остальных зарядов, равна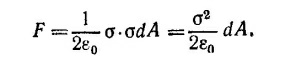
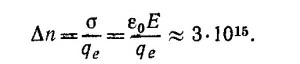
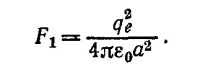
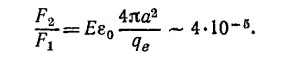
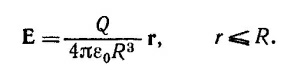

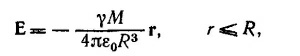
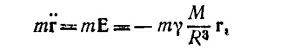
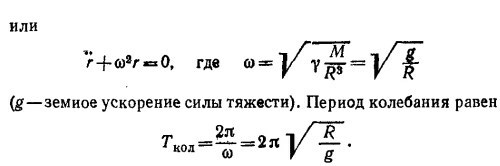

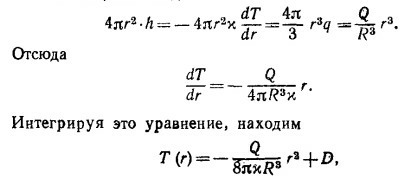
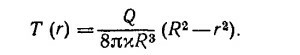
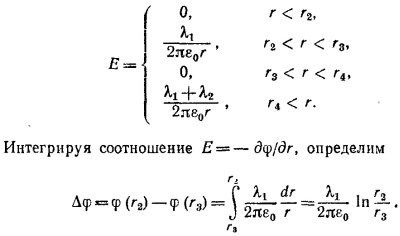
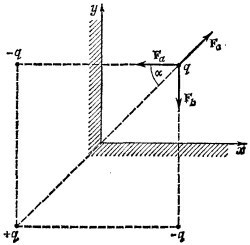 6.1. Полуплоскости, о которых идет речь в условии,—эквипотенциальные поверхности системы четырех зарядов, изображенных на рисунке. Для решения необходимо найти равнодействующую сил:
6.1. Полуплоскости, о которых идет речь в условии,—эквипотенциальные поверхности системы четырех зарядов, изображенных на рисунке. Для решения необходимо найти равнодействующую сил: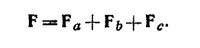

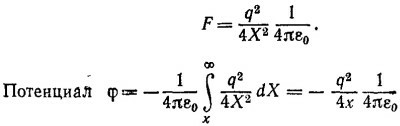
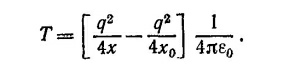
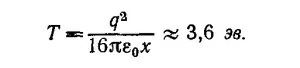
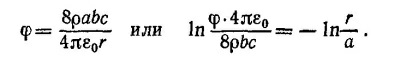
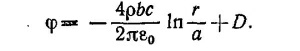
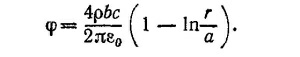
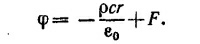

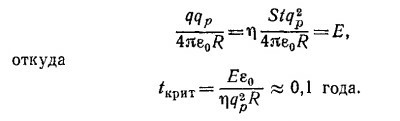
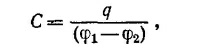
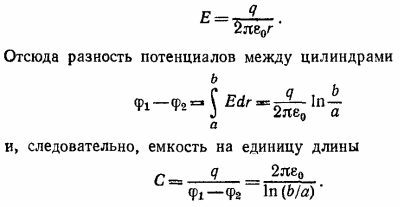
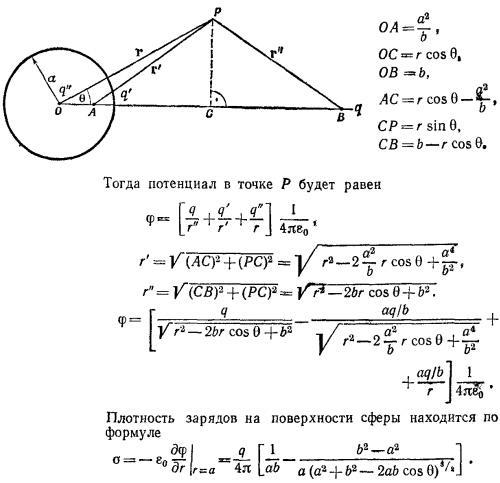
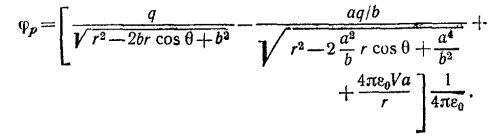
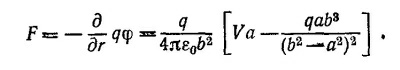
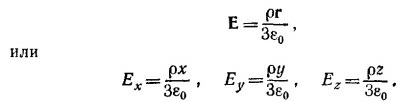 6.7. Покажем, что суммарная поверхностная плотность зарядов, создаваемая двумя противоположно заряженными шарами, слабо сдвинутыми друг относительно друга, действительно меняется как A cos θ. Пусть объемная плотность зарядов каждого из шаров по абсолютной величине равна ρ. Поверхностная плотность при θ = 0 (см. рисунок) равна ρd, а при θ≠0, σ(θ) = ρ/h(θ), где h(θ)=d cosθ; таким образом, σ(θ)= A cos θ, где A=ρd.
6.7. Покажем, что суммарная поверхностная плотность зарядов, создаваемая двумя противоположно заряженными шарами, слабо сдвинутыми друг относительно друга, действительно меняется как A cos θ. Пусть объемная плотность зарядов каждого из шаров по абсолютной величине равна ρ. Поверхностная плотность при θ = 0 (см. рисунок) равна ρd, а при θ≠0, σ(θ) = ρ/h(θ), где h(θ)=d cosθ; таким образом, σ(θ)= A cos θ, где A=ρd.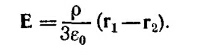
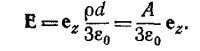
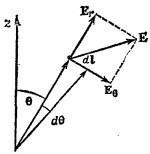 6.8. а) Угол θ определим так же, как в «Лекциях» (вып. 5, стр. 112). Угол φ характеризует положение плоскости, проведенной через векторы р и r. От этого угла не зависят ни потенциал, ни поле. Согласно формуле (6.11) «Лекций» (вып. 5, стр. 112),
6.8. а) Угол θ определим так же, как в «Лекциях» (вып. 5, стр. 112). Угол φ характеризует положение плоскости, проведенной через векторы р и r. От этого угла не зависят ни потенциал, ни поле. Согласно формуле (6.11) «Лекций» (вып. 5, стр. 112),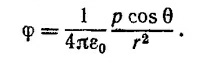
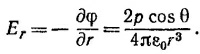
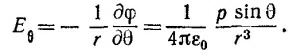
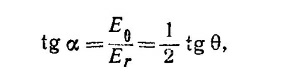
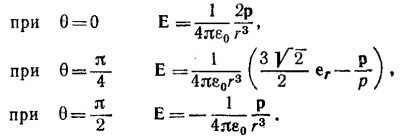
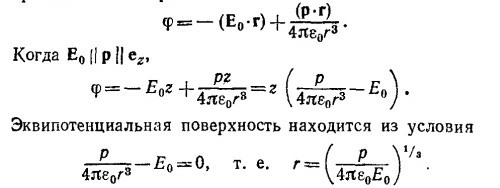
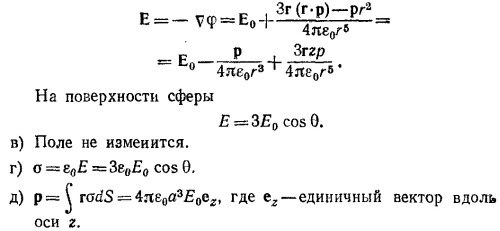
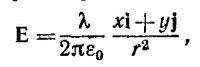
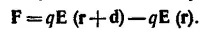
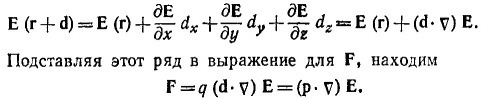
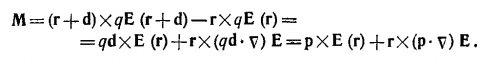
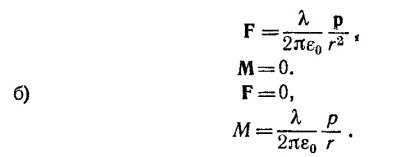
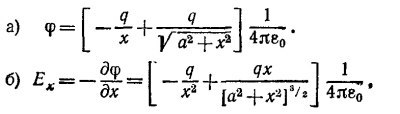
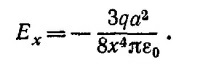

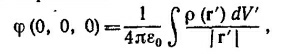
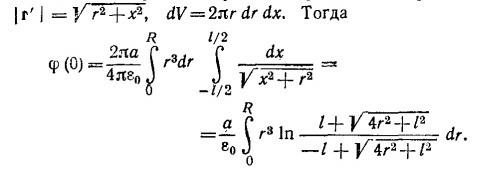
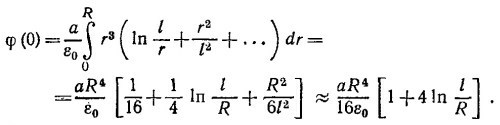
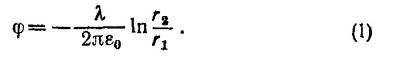
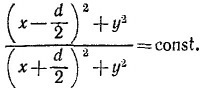
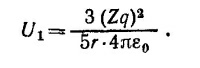
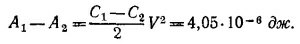
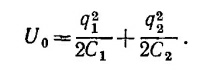
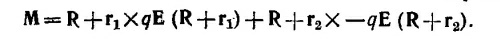
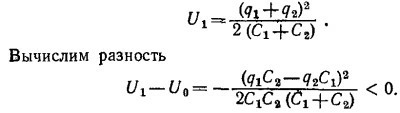
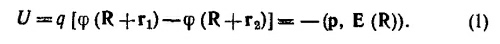
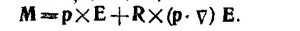
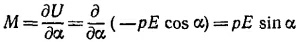
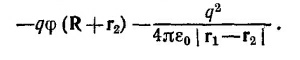
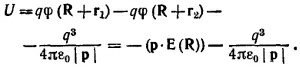
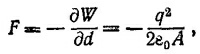
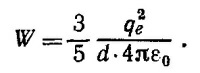
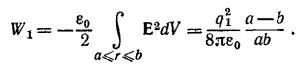

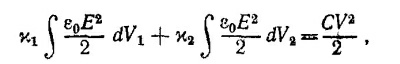
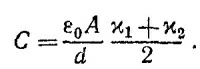
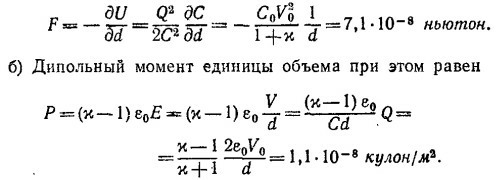
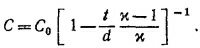
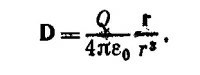
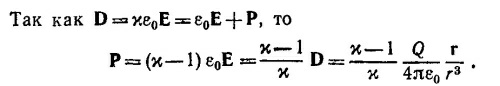
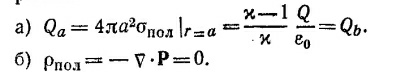
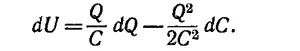
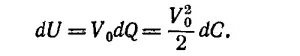
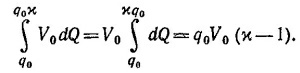
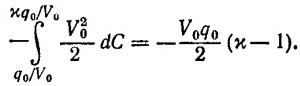
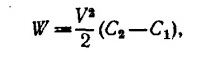
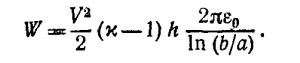
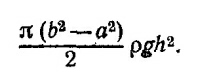
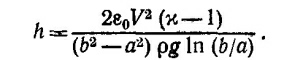
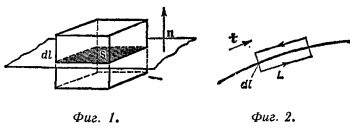 10.7. Граничные условия на границе раздела двух сред (1) и (2) имеют вид Е1t= Е2t , D1n =D2n или Е1n/x1 = Е2n/x2, где индексами n и t помечены нормальные и тангенциальные к поверхности составляющие векторов. Эти граничные условия следуют из уравнений Максвелла divD = 0 и VXE = 0. Действительно, рассмотрим произвольную поверхность раздела двух сред (фиг. 1). Выберем произвольным образом направление внешней нормали n к этой поверхности и условимся обозначать индексами 1 и 2 величины, относящиеся соответственно к нижней и верхней средам. Выделим мысленно около рассматриваемой точки поверхности прямую призму с образующими dl, перпендикулярными поверхности. Пусть эта призма вырезает на поверхности элемент S столь малый, что его можно считать плоским. По теореме Гаусса поток вектора электрической индукции через поверхность призмы должен равняться нулю ∫ D.dS= ∫ divD·dV =0. При стремлении dl к нулю поток вектора D через боковую поверхность призмы также будет стремиться к нулю. Для потока же через верхнее и нижнее основание призмы получаем
10.7. Граничные условия на границе раздела двух сред (1) и (2) имеют вид Е1t= Е2t , D1n =D2n или Е1n/x1 = Е2n/x2, где индексами n и t помечены нормальные и тангенциальные к поверхности составляющие векторов. Эти граничные условия следуют из уравнений Максвелла divD = 0 и VXE = 0. Действительно, рассмотрим произвольную поверхность раздела двух сред (фиг. 1). Выберем произвольным образом направление внешней нормали n к этой поверхности и условимся обозначать индексами 1 и 2 величины, относящиеся соответственно к нижней и верхней средам. Выделим мысленно около рассматриваемой точки поверхности прямую призму с образующими dl, перпендикулярными поверхности. Пусть эта призма вырезает на поверхности элемент S столь малый, что его можно считать плоским. По теореме Гаусса поток вектора электрической индукции через поверхность призмы должен равняться нулю ∫ D.dS= ∫ divD·dV =0. При стремлении dl к нулю поток вектора D через боковую поверхность призмы также будет стремиться к нулю. Для потока же через верхнее и нижнее основание призмы получаем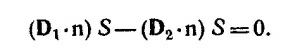
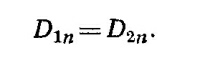
 Покажем теперь, что на границе раздела двух сред касательная составляющая вектора напряженности электрического поля Е непрерывна. С этой целью выберем около произвольной поверхности (на фиг. 2 ее сечение плоскостью рисунка изображено сплошной линией) контур в виде прямоугольной рамки, боковые стороны dl которой нормальны к поверхности раздела сред. Выберем размеры этого контура столь малыми, чтобы поверхность раздела двух сред можно было считать плоской. Мысленно «натянем» на эту рамку стоксову поверхность. Тогда по теореме Стокса
Покажем теперь, что на границе раздела двух сред касательная составляющая вектора напряженности электрического поля Е непрерывна. С этой целью выберем около произвольной поверхности (на фиг. 2 ее сечение плоскостью рисунка изображено сплошной линией) контур в виде прямоугольной рамки, боковые стороны dl которой нормальны к поверхности раздела сред. Выберем размеры этого контура столь малыми, чтобы поверхность раздела двух сред можно было считать плоской. Мысленно «натянем» на эту рамку стоксову поверхность. Тогда по теореме Стокса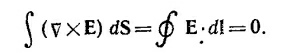
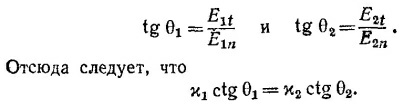
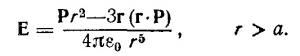
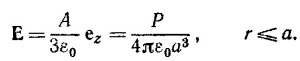
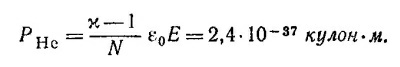

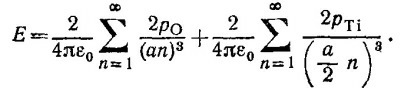
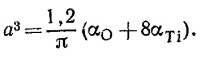
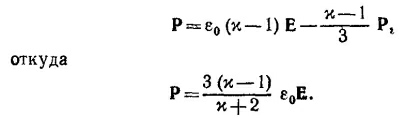
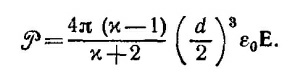
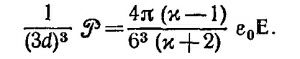
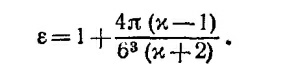
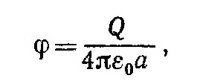
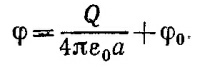
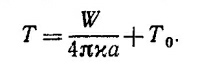
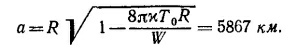
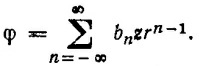
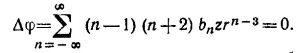
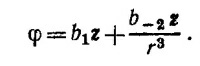
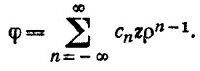
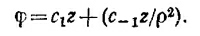
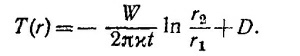
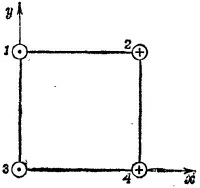 13.1. а) Напряженность магнитного поля, создаваемого током, текущим по бесконечному прямому проводу, на расстоянии r от последнего равна В = (I х еr)/2πε0с2a, где еr — единичный вектор в направлении радиуса-вектора, лежащего в плоскости, перпендикулярной проводу. В центре квадрата компоненты вектора напряженности магнитного поля равны Bу = 2I/πε0с2a = 8·10–5 вебер/м2, Вх = 0 (см. рисунок). Вектор В, следовательно, направлен вертикально вверх.
13.1. а) Напряженность магнитного поля, создаваемого током, текущим по бесконечному прямому проводу, на расстоянии r от последнего равна В = (I х еr)/2πε0с2a, где еr — единичный вектор в направлении радиуса-вектора, лежащего в плоскости, перпендикулярной проводу. В центре квадрата компоненты вектора напряженности магнитного поля равны Bу = 2I/πε0с2a = 8·10–5 вебер/м2, Вх = 0 (см. рисунок). Вектор В, следовательно, направлен вертикально вверх.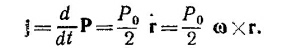
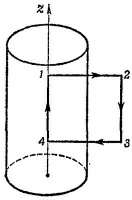 Выберем контур интегрирования так, как показано на рисунке, и воспользуемся теоремой Стокса. Магнитное поле по соображениям симметрии направлено вдоль оси цилиндра. Находим, что вне цилиндра В = 0. Поле на оси цилиндра равно
Выберем контур интегрирования так, как показано на рисунке, и воспользуемся теоремой Стокса. Магнитное поле по соображениям симметрии направлено вдоль оси цилиндра. Находим, что вне цилиндра В = 0. Поле на оси цилиндра равно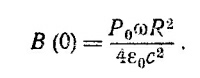
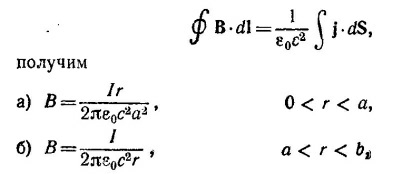
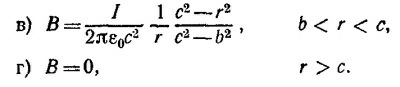
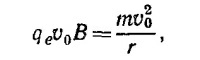
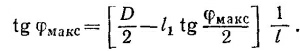
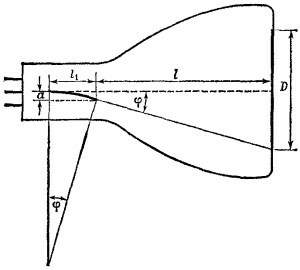 Радиус окружности как функция параметров трубки и угла отклонения есть r = /1/sin φмакс.
Радиус окружности как функция параметров трубки и угла отклонения есть r = /1/sin φмакс.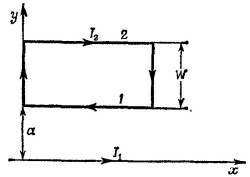 13.5. а) При определении силы, действующей на рамку с током, будем исходить из того, что на элемент тока длиной dl действует сила, равная dF = I2dI x B. Проинтегрируем это выражение по контуру рамки. Ясно, что силы, действующие на участки рамки, перпендикулярные проводу, равны по величине и противоположны по направлению. Их результирующая равна нулю. Сила, реально действующая на рамку, равна сумме сил, действующих на участки, параллельные проводу. Так как магнитное поле, создаваемое проводом на расстоянии у от него, равно
13.5. а) При определении силы, действующей на рамку с током, будем исходить из того, что на элемент тока длиной dl действует сила, равная dF = I2dI x B. Проинтегрируем это выражение по контуру рамки. Ясно, что силы, действующие на участки рамки, перпендикулярные проводу, равны по величине и противоположны по направлению. Их результирующая равна нулю. Сила, реально действующая на рамку, равна сумме сил, действующих на участки, параллельные проводу. Так как магнитное поле, создаваемое проводом на расстоянии у от него, равно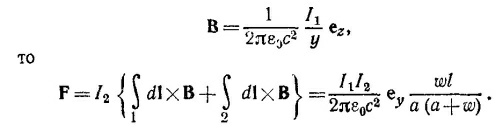
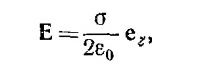
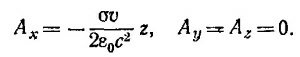
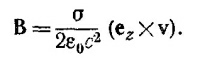
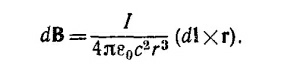
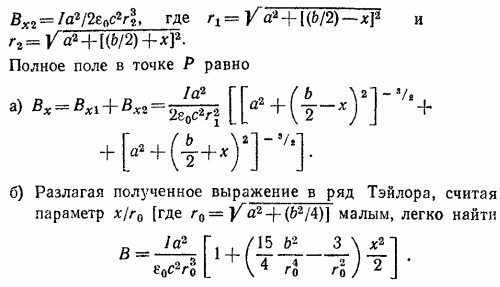
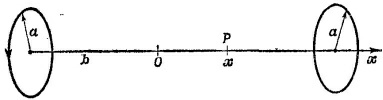
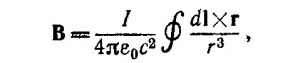
 где интегрирование ведется по всем сторонам рамки. Если представить вектор r в виде суммы двух векторов, один из которых направлен вдоль оси х и имеет длину, равную х, а другой расположен в плоскости уz, то можно записать
где интегрирование ведется по всем сторонам рамки. Если представить вектор r в виде суммы двух векторов, один из которых направлен вдоль оси х и имеет длину, равную х, а другой расположен в плоскости уz, то можно записать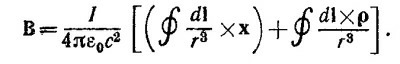
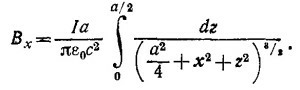
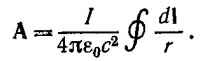
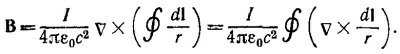
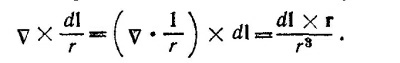
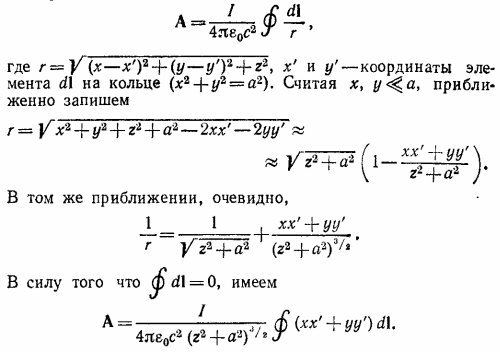
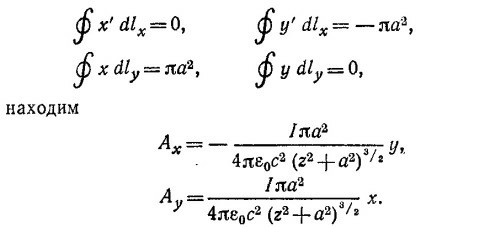
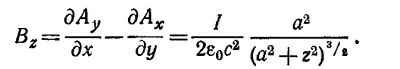
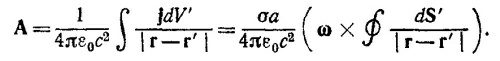
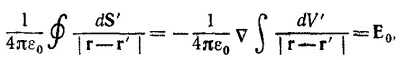

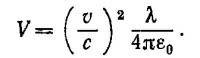
 б) Пусть в нашем распоряжении имеется очень чувствительный вольтметр, с помощью которого можно замерять разности потенциалов в 10-10 в. Из найденного выражения для V следует, что величина V тем выше, чем больше λ —заряд, приходящийся на единицу длины цилиндра. Пусть плотность поверхностных зарядов σ на цилиндре достаточно велика, скажем такая же; как на проводящей сфере с радиусом в а=1 м, заряженной до потенциала в V0 = 106 в. Тогда σ= εoVo/a и λ= 2πε0V0b/а.
б) Пусть в нашем распоряжении имеется очень чувствительный вольтметр, с помощью которого можно замерять разности потенциалов в 10-10 в. Из найденного выражения для V следует, что величина V тем выше, чем больше λ —заряд, приходящийся на единицу длины цилиндра. Пусть плотность поверхностных зарядов σ на цилиндре достаточно велика, скажем такая же; как на проводящей сфере с радиусом в а=1 м, заряженной до потенциала в V0 = 106 в. Тогда σ= εoVo/a и λ= 2πε0V0b/а. 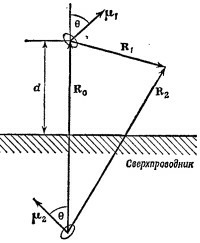 6
6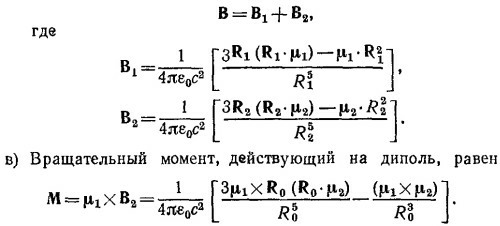
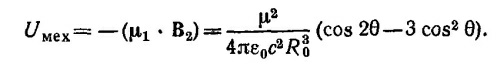
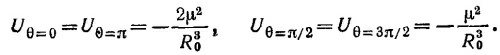
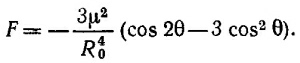
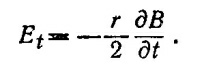
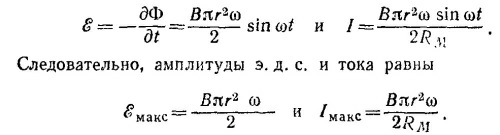
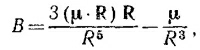
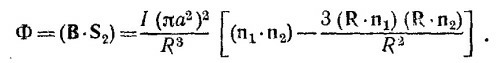
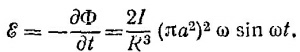
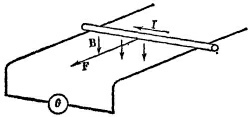 17.4. а) Провод движется равноускоренно. Действительно, из закона Ампера сила, действующая на провод, равна IBd. Решая уравнение движения для провода с начальным условием v(t)|t=0 = 0, получаем v = (IBd/m) t.
17.4. а) Провод движется равноускоренно. Действительно, из закона Ампера сила, действующая на провод, равна IBd. Решая уравнение движения для провода с начальным условием v(t)|t=0 = 0, получаем v = (IBd/m) t. 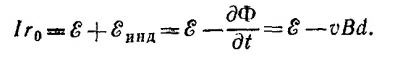
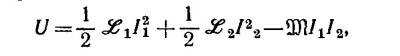
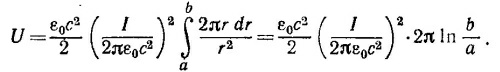
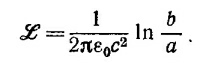
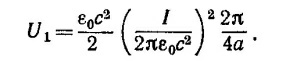
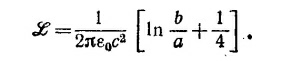
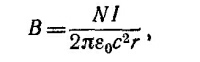
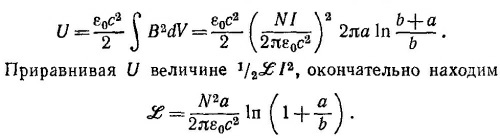
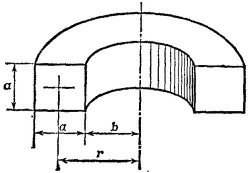 б) Для определения взаимной индукции системы, состоящей из тороидальной катушки и прямолинейного провода, вычислим Ф0—магнитный поток, создаваемый проводом через поперечное сечение тороида. Так как напряженность магнитного поля В, создаваемая прямолинейным проводником на расстоянии r от него, равна В = I1/2πε0с2r (силовые линии поля В представляют собой концентрические окружности), то магнитный поток через один виток тороидальной катушки равен
б) Для определения взаимной индукции системы, состоящей из тороидальной катушки и прямолинейного провода, вычислим Ф0—магнитный поток, создаваемый проводом через поперечное сечение тороида. Так как напряженность магнитного поля В, создаваемая прямолинейным проводником на расстоянии r от него, равна В = I1/2πε0с2r (силовые линии поля В представляют собой концентрические окружности), то магнитный поток через один виток тороидальной катушки равен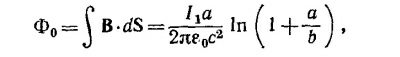
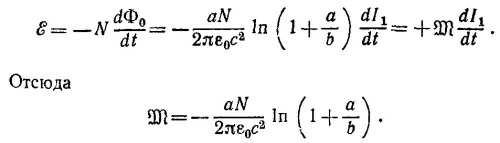
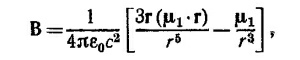
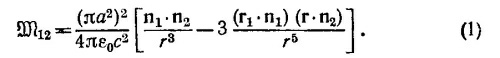
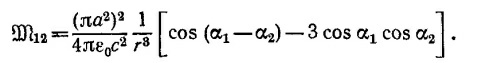
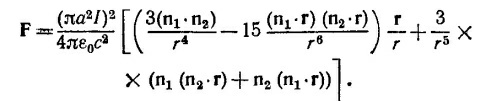
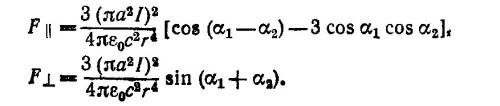
 в) Если изменить направление токов сразу в двух витках, то сила не изменится, если изменить его только в одном витке, то сила изменит знак, так как при этом изменится направление одного из векторов n на противоположное.
в) Если изменить направление токов сразу в двух витках, то сила не изменится, если изменить его только в одном витке, то сила изменит знак, так как при этом изменится направление одного из векторов n на противоположное.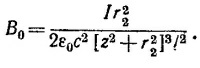
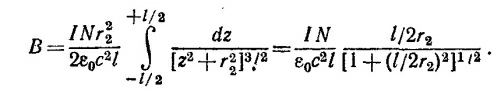
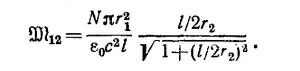
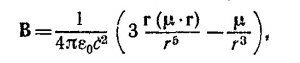
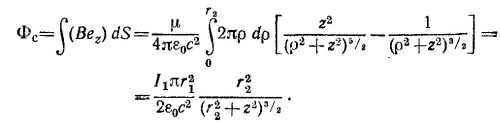
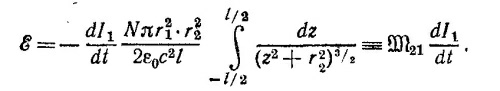
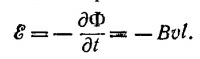
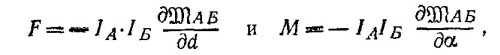
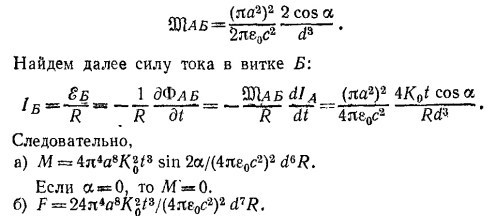

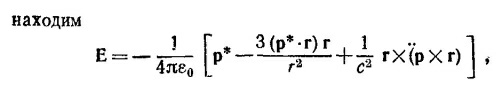
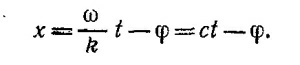
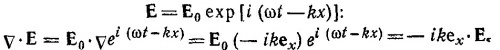
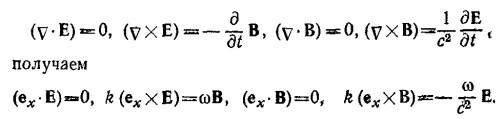
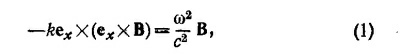
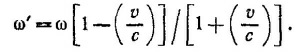

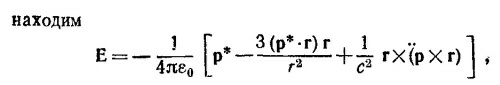
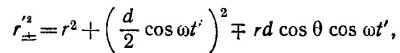
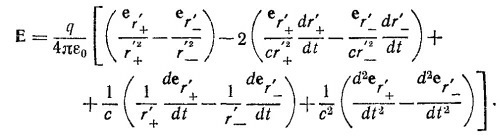
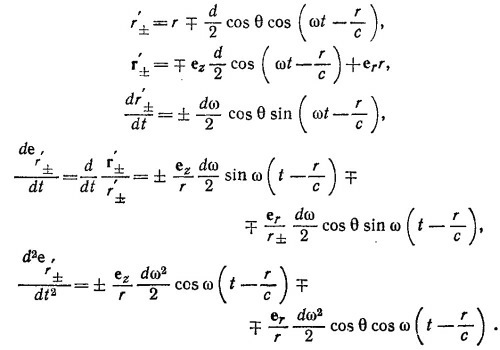
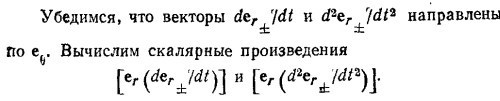
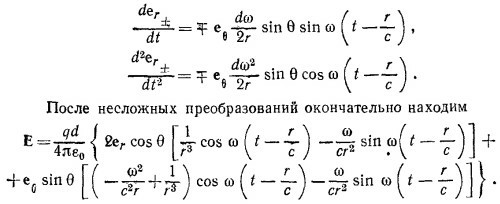
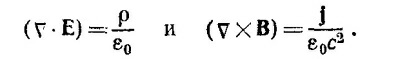
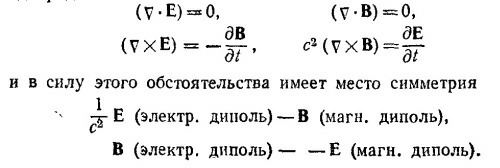
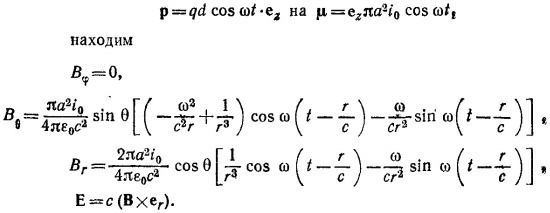
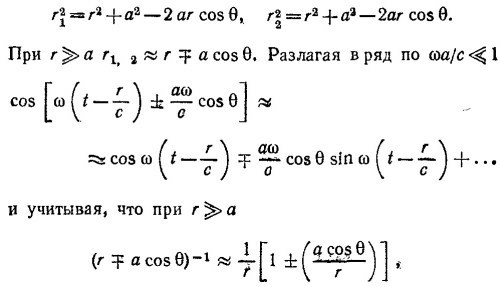
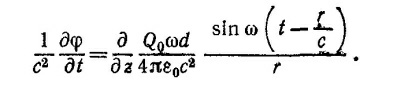
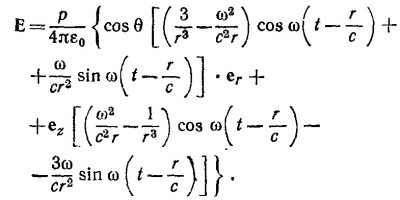
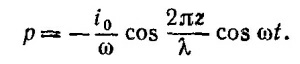

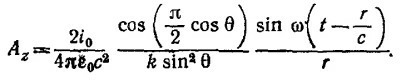
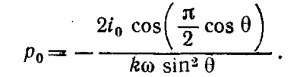
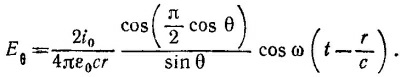
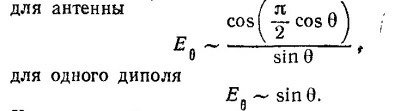
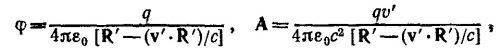
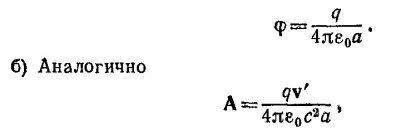
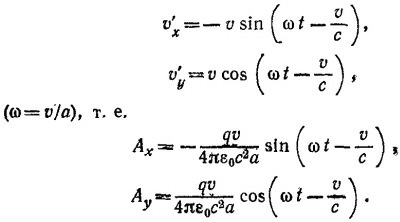
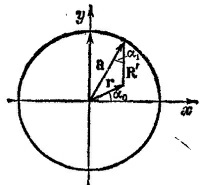 в) Определим потенциалы в точке, расположенной вблизи центра круга (r –радиус-вектор этой точки, см. рисунок). Обозначая через α0 угол между r и осью х, запишем
в) Определим потенциалы в точке, расположенной вблизи центра круга (r –радиус-вектор этой точки, см. рисунок). Обозначая через α0 угол между r и осью х, запишем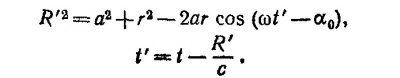
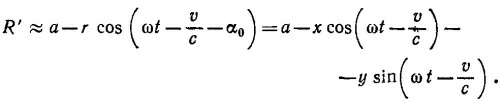
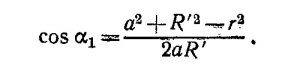
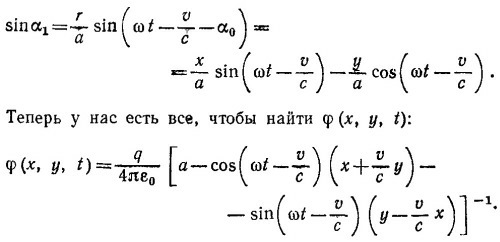
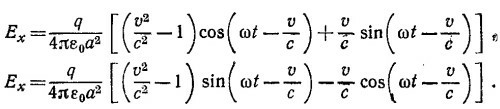
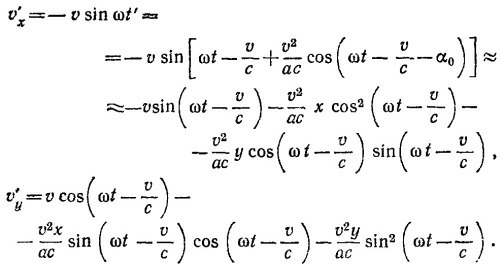
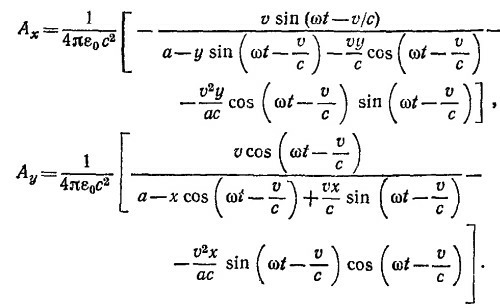
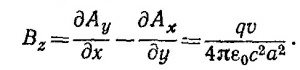
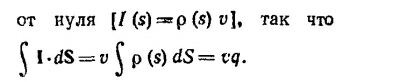
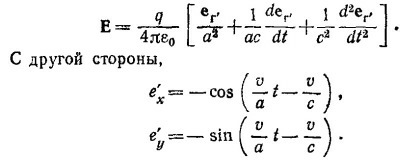
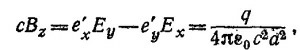
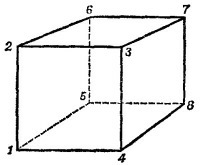 22.1. а) Пусть ток втекает в узел 1 (см. рисунок), а вытекает из узла 7. В силу симметрии системы потенциалы точек 2, 5, 4 равны. Также равны между собой потенциалы точек 6, 3 и 8. В итоге получим электрическую схему следующего типа:
22.1. а) Пусть ток втекает в узел 1 (см. рисунок), а вытекает из узла 7. В силу симметрии системы потенциалы точек 2, 5, 4 равны. Также равны между собой потенциалы точек 6, 3 и 8. В итоге получим электрическую схему следующего типа: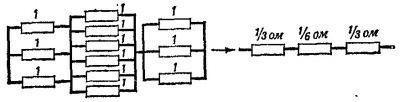
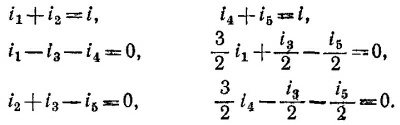
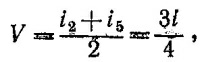
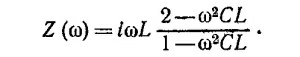
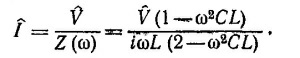
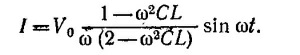
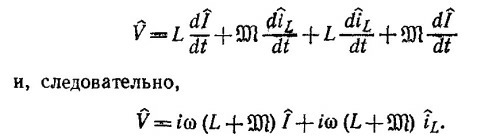
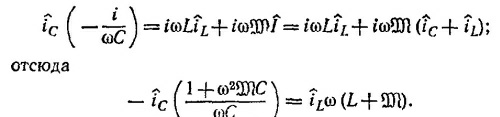
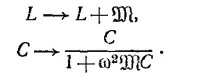
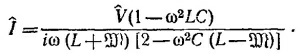
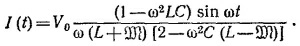
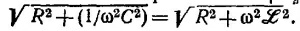
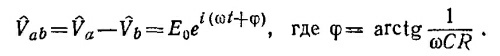

 В этом случае амплитуда разности потенциалов перестает зависеть от частоты лишь при очень малых или очень больших частотах. Качественный ход фазы разности потенциалов остается прежним.
В этом случае амплитуда разности потенциалов перестает зависеть от частоты лишь при очень малых или очень больших частотах. Качественный ход фазы разности потенциалов остается прежним.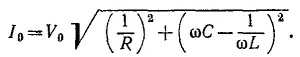
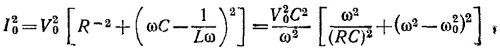
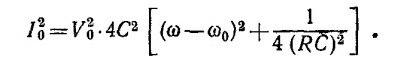
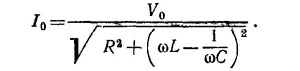
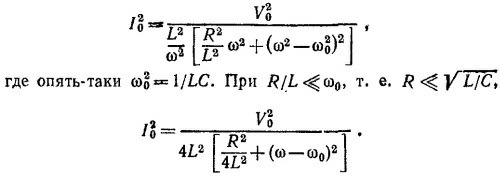
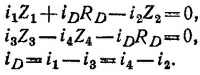
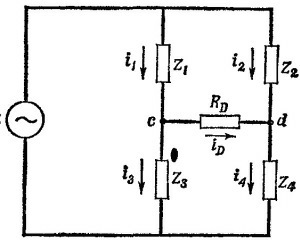 Условие компенсации имеет вид ¡D=0. Отсюда i1 = i3 и i2 = i4 и, следовательно, Z1Z4=Z2Z3,т. e. (¡ωL + Ra)/(iωC + Rb–1)=R2. Определяя вещественную и мнимую части, находим
Условие компенсации имеет вид ¡D=0. Отсюда i1 = i3 и i2 = i4 и, следовательно, Z1Z4=Z2Z3,т. e. (¡ωL + Ra)/(iωC + Rb–1)=R2. Определяя вещественную и мнимую части, находим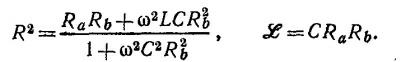
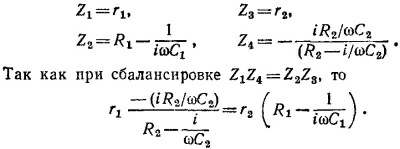
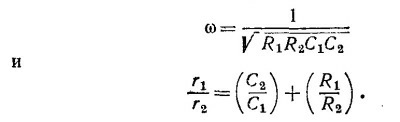
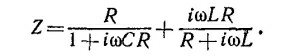
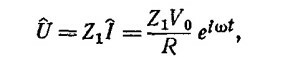
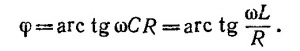
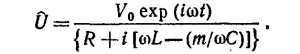
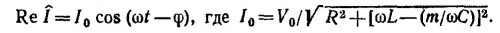
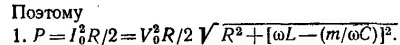
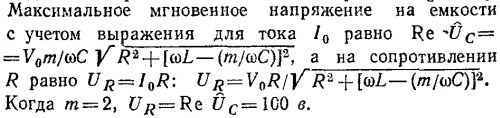
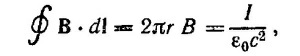
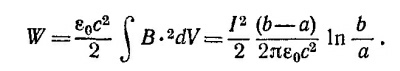
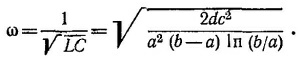
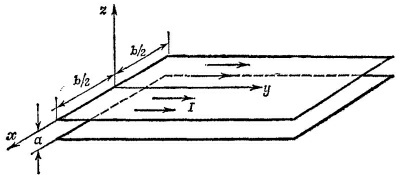 24.2. Напряженность магнитного поля бесконечной проводящей плоскости, по которой течет ток, вычислялась в задаче 14.1.
24.2. Напряженность магнитного поля бесконечной проводящей плоскости, по которой течет ток, вычислялась в задаче 14.1.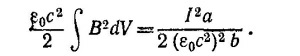
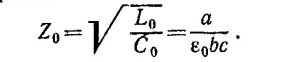
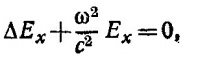
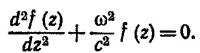
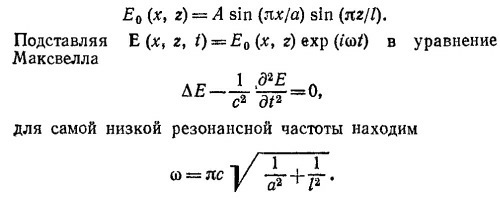
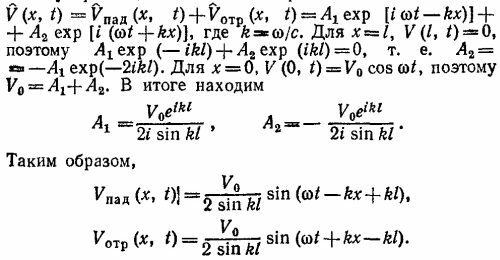
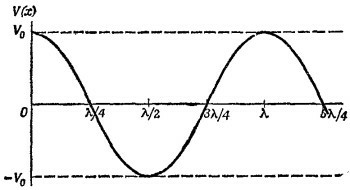 Обратим внимание на то, что при kl = πn (n —целое число) амплитуды волн, согласно нашим формулам, обращаются в бесконечность. Физически это означает наступление резонанса —частота источника сравнивается с одной из резонансных частот отрезка кабеля. Амплитуда колебаний при резонансе на самом деле безусловно конечна: величина ее определяется омическими потерями, которыми мы пренебрегли.
Обратим внимание на то, что при kl = πn (n —целое число) амплитуды волн, согласно нашим формулам, обращаются в бесконечность. Физически это означает наступление резонанса —частота источника сравнивается с одной из резонансных частот отрезка кабеля. Амплитуда колебаний при резонансе на самом деле безусловно конечна: величина ее определяется омическими потерями, которыми мы пренебрегли.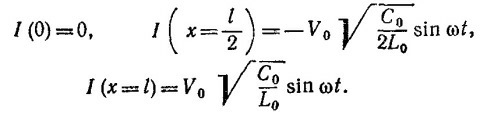
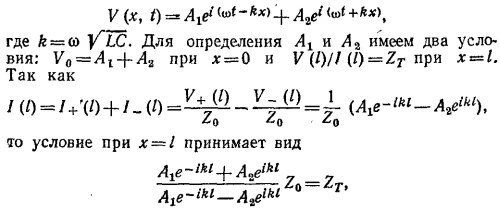
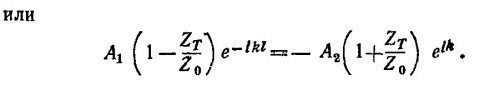
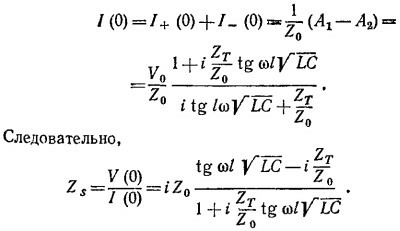
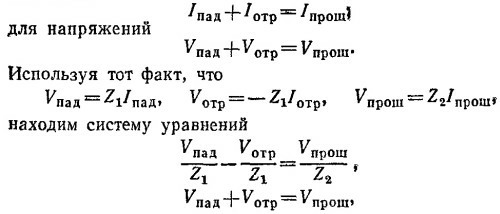
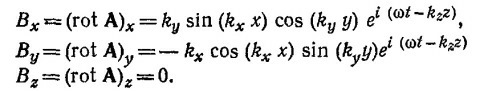
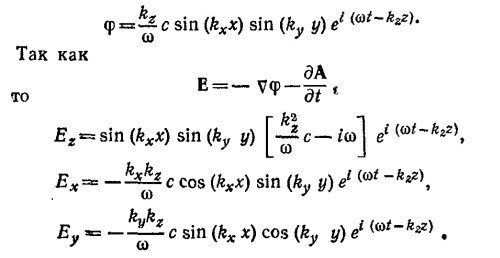
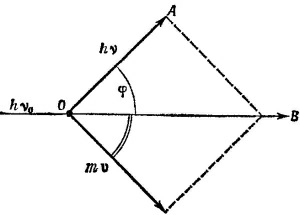 25.2. Начальные условия: электрон покоился (его энергия была равна m0, а импульс—нулю), фотон налетал с энергией hv0 и импульсом hv0. После соударения энергия электрона стала равна m, а импульс mv, где m = m0/√1—β2. Энергию фотона после соударения обозначим hv, а его импульс hv. Напишем законы сохранения энергии и импульса
25.2. Начальные условия: электрон покоился (его энергия была равна m0, а импульс—нулю), фотон налетал с энергией hv0 и импульсом hv0. После соударения энергия электрона стала равна m, а импульс mv, где m = m0/√1—β2. Энергию фотона после соударения обозначим hv, а его импульс hv. Напишем законы сохранения энергии и импульса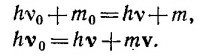
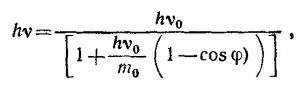
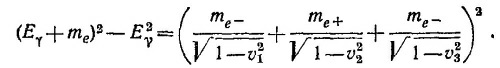
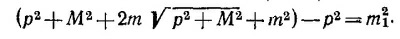
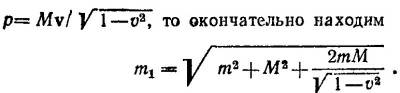
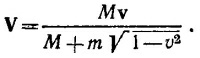
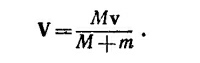
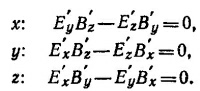
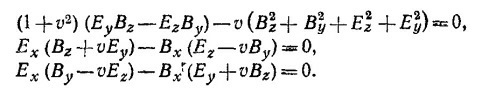
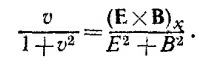
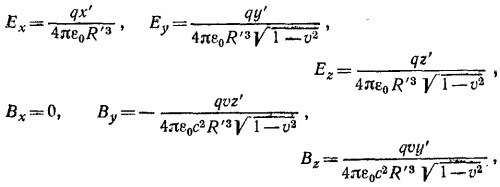
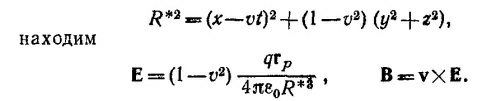
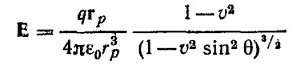
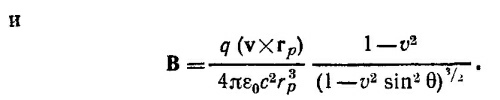
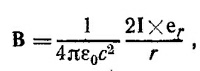
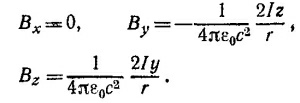
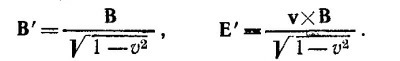
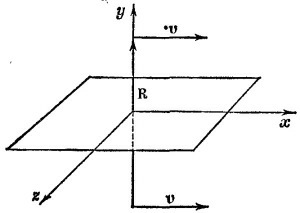 26.8. Вектор напряженности электрического поля Е, создаваемого бесконечной равномерно заряженной плоскостью, из соображений симметрии направлен перпендикулярно этой плоскости. Величину же его легко определить с помощью теоремы Гаусса. В результате Е = (σ/2ε0) еу, где еу—единичный вектор в направлении оси у (см. рисунок).
26.8. Вектор напряженности электрического поля Е, создаваемого бесконечной равномерно заряженной плоскостью, из соображений симметрии направлен перпендикулярно этой плоскости. Величину же его легко определить с помощью теоремы Гаусса. В результате Е = (σ/2ε0) еу, где еу—единичный вектор в направлении оси у (см. рисунок).