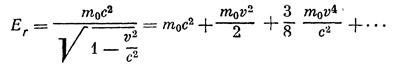Главная >> В мире больших скоростей >> Специальная теория относительности 18. Энергия
Под энергией тела физики понимают запас работы, заключенный в теле. Работа в физике — это любое преодоление воздействия. Когда мяч разбивает окно, он совершает работу. У летевшего мяча был запас энергии, часть которой была затрачена на то, чтобы разбить стекло.
Классическая механика утверждает, что энергия свободного тела обусловлена только его движением, это так называемая кинетическая энергия. Если тело с массой mо движется со скоростью v, то его кинетическая энергия Е выражается в классической физике известной формулой
Е = mov2/2 (6)
(индексом нуль при m мы подчеркиваем, что масса не зависит от скорости движения тела).
Кинетическая энергия определяется скоростью тела. Скорость же, как известно, в свою очередь, зависит от системы отсчета. Отсюда видно, что кинетическая энергия тела зависит от системы отсчета. В каждой системе отсчета энергия имеет свое значение. Следовательно, энергия даже в классической механике является относительной величиной.
С относительностью кинетической энергии мы часто встречаемся в повседневной жизни. Например, кинетическая энергия маленького камня, брошенного в воздух, невелика относительно Земли. Относительно же быстро мчащейся автомашины кинетическая энергия этого камня уже достаточна для того, чтобы разбить ветровое стекло автомашины и даже поранить водителя. Известны случаи, когда вылетевшие из-под колес передней автомашины камушки причиняли серьезные повреждения движущейся следом автомашине.
Что говорит теория относительности об энергии свободного тела? Выше мы видели, что поправки, которые теория относительности вносит в классическую механику, при малых скоростях совершенно незначительны, только для больших скоростей они становились существенными. Казалось бы, можно ожидать, что так же будет обстоять дело и с энергией: при малых скоростях формула для энергии в теории относительности будет совпадать с формулой (6); при больших скоростях будут наблюдаться отличия. Однако эти ожидания в действительности не оправдываются.
Если масса покоя тела то и скорость v, то энергия его в теории относительности выражается формулой
Er = m0c2/√(1 - v2/c2) = mc2 (7)
(индексом r у Е мы подчеркиваем, что здесь мы имеем дело с выведенным в теории относительности релятивистским выражением для энергии).
Формула (7) значительно отличается от формулы (6) даже для покоящегося тела. Если скорость v равна нулю, формула классической механики дает кинетическую энергию, равную нулю. В релятивистском выражении при v = 0 энергия равна не нулю, а m0с2. Релятивистскую энергию покоящегося тела назовем энергией оггокоя и обозначим через Ео. (Сравнение классической кинетической энергии тела с релятивистской приведено в табл. 7.)
E0 = m0c2 (8)
Простые расчеты показывает, что энергия покоя очень велика даже для малых тел. Так, например, для тела, масса покоя которого равна 1 г, энергия покоя составляет 99 180 000 миллионов килограммометров. За счет этой энергии можно было бы поднять груз весом в 918 000 m на высоту 10 км. Такой колоссальный запас энергии содержит в себе 1 г вещества — на это указывает нам теория относительности. Классическая же физика не может сказать ничего о существовании подобной энергии.
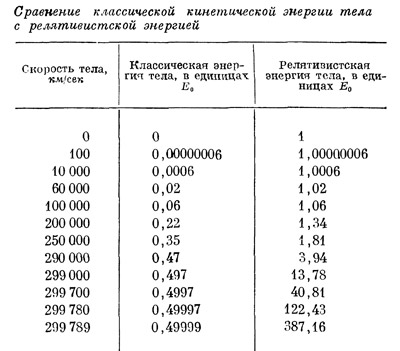
В табл. 7 за единицу энергии выбрана энергия покоя Ео. Если скорость тела приближается к скорости света, классическая кинетическая энергия, вычисленная согласно формуле классической физики, становится равной половине энергии покоя, т. е. половине той энергии, которую согласно теории относительности имеет уже покоящееся тело.
По теории относительности в случае, когда скорость тела очень близка к скорости света, энергия тела становится неограниченно большой. Другими словами: релятивистская энергия тела может стать сколь угодно большой, если только скорость тела достаточно близка к скорости света. На основе данных табл. 7 составлены графики рис. 42.
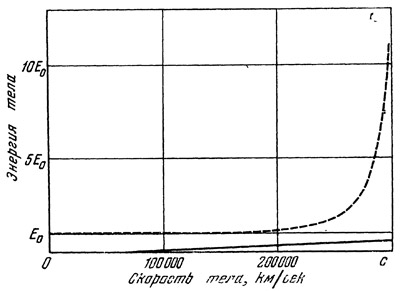 Рис. 42. Сравнение классической энергии тела (сплошная линия) и релятивистской энергии (пунктирная линия). E0 обозначает энергию покоя тела Рис. 42. Сравнение классической энергии тела (сплошная линия) и релятивистской энергии (пунктирная линия). E0 обозначает энергию покоя тела
Выражение для релятивистской энергии может быть записано в виде бесконечного ряда. Первые члены этого ряда таковы:
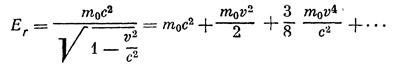
Если скорость v мала по сравнению со скоростью света, то все члены, начиная c третьего, будут очень малы (в знаменателе стоит скорость света), и мы можем их не учитывать. Релятивистская энергия тела, движущегося с малой скоростью, достаточно точно выражается формулой
Er = m0c2 + m0v2/2
где mос2 — энергия покоя.
Таким образом, энергия тела равняется сумме энергии покоя и классической кинетической энергии.
В классической физике нас интересует только разность энергий. Вычитая, например, начальную энергию тела, участвующего в каком-либо процессе, из его конечной энергии, получаем изменение энергии в данном процессе. Если масса покоя тела mо не изменяется в процессе, то при образовании разностей энергий первый член в выражении анергии выпадает. Описывая такие процессы, можно уже с самого начала не записывать этот член. Отсюда видно, что классическое выражение для энергии можно использовать при энергетических вычислениях только тогда, когда выполняются два условия:
а) скорость рассматриваемого тела мала по сравнению со скоростью света;
б) массы покоя участвующих в исследуемом процессе тел не изменяются.
Если одно из этих условий не выполнено, то при вычислениях необходимо пользоваться релятивистским выражением энергии (7).
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|





 Рис. 42. Сравнение классической энергии тела (сплошная линия) и релятивистской энергии (пунктирная линия). E0 обозначает энергию покоя тела
Рис. 42. Сравнение классической энергии тела (сплошная линия) и релятивистской энергии (пунктирная линия). E0 обозначает энергию покоя тела