Главная >> Лекции по ядерной физике

1.5. Закономерность и характеристики радиоактивного распада

1.5.1. В зависимости от вида испускаемых возбуждённым ядром частиц известны следующие виды радиоактивного распада:
- α-распад, то есть распад, сопровождающийся испусканием возбуж­дёнными ядрами α-частиц (массой 4 а.е.м. с зарядом z = 2), по существу являющихся лишёнными внешних электронов ядрами атомов гелия, а потому часто обозначаемых ₄Не²;
- β-распад, то есть распад, сопровождающийся испусканием быстрых электронов или позитронов; эти два вида частиц равной массы отличаются только знаками электрического заряда: электроны имеют элементарный отрицательный заряд, а позитроны - положительный заряд той же величины; отсюда - общее название их - β-частицы;
- γ-распад - то есть распад, сопровождающийся испусканием жестко­го электромагнитного излучения с частотой выше частоты рентгеновского излучения, называемого гамма-излучением;
- нейтронный распад - распад, сопровождающийся испусканием воз­буждённым ядром нейтронов; благодаря этому виду радиоактивного распада в ядерном реакторе появляются так называемые запаздывающие нейтроны, имеющие большое значение для управляемости реактора.


1.5.2. Независимо от вида радиоактивный распад подчиняется единой закономерности:
Скорость радиоактивного распада  (количество ежесекундно испускаемых  частиц, равное числу ежесекундно распадающихся ядер) прямо пропорциональна только наличному в данный момент количеству радиоактивных ядер.
dN/dt = -λN(t) ,     (1.5.1)
где:   N(t),см^-3 - ядерная концентрация радиоактивных ядер в рассматри­ваемый момент времени t;
dN/dt,см^-3с^-1 – мгновенное значение скорости радиоактивного распада, то есть коли­чество распадающихся в 1 см³ ядер за 1 с (в данный момент времени);
λ, c^-1 - постоянная радиоактивного распада, имеющая смысл доли ежесекундно распадающихся радиоактивных ядер от общего наличного их количества в рассматриваемый момент времени.
Выражение (1.5.1) называют законом радиоактивного распада в дифференциальной форме.
Если проинтегрировать дифференциальное уравнение (1.5.1) при на­чальном условии (t = 0  N = N_o), то получается:
N(t) = N_o exp(-λt),      (1.5.2)
 то есть концентрация нераспавшихся радиоактивных ядер во времени падает по экспоненциальному закону, и темп радиоактивного распада определяется только одной величиной - величиной постоянной радиоактивного распада.
Формулу (1.5.2) называют законом радиоактивного распада в ин­тегральной форме.


1.5.3. Часто в качестве характеристики интенсивности радиоактив­ного распада используется не сама постоянная радиоактивного распада λ, а обратная ей величина T = 1/λ, называемая периодом радиоактивного распада.
Период радиоактивного распада - это время, в течение которого количество радиоактивных ядер уменьшается в е = 2.7182818... раз.
Действительно,  N(T)/No = exp(-T_1/2/T) = e^-1 = 1/e.
Ещё чаще в практических расчётах и оценках пользуются не периодом распада, а периодом полураспада (Т_1/2), под которым понимается время, в течение которого количество нераспавшихся радиоактивных ядер уменьша­ется ровно в 2 раза.
Нетрудно увидеть, что Т и Т_1/2 - пропорционально взаимосвязанные характеристики. Действительно, при t = T_1/2   N(T_1/2) / N_o = 1/2, то есть:
exp(-T_1/2/T) = 1/2, откуда Т_1/2/T = ln2 ≈ 0.693, а значит:
Т _1/2 ≈ 0.693 Т,  или  Т ≈ 1.44 Т_1/2                          (1.5.3)


1.5.4. Экспонента, как известно, - кривая асимптотическая, поэтому падающая экспонента может обращаться в нуль только теоретически (при бесконечно большом значении t). Поэтому, интересуясь вопросом о време­ни практически полного распада радиоактивных ядер, следует условиться, при каком количестве оставшихся нераспавшимися радиоактивных ядер рас­пад считать практически полным.
Если считать радиоактив­ный распад практически завершившимся тогда, когда осталось не более 1% от начального количества нераспавшихся ядер, то, как хорошо видно из графика (рис.1.3), время практически полного распада радиоактивного вещества составляет 6-7 периодов его полураспада или 4-5 периодов рас­пада Т.

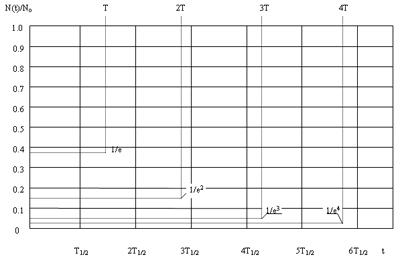Рис.1.3. Экспоненциальный закон радиоактивного распада.

СМОТРИТЕ ТАКЖЕ: