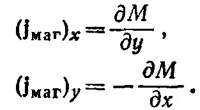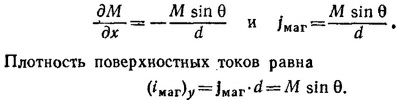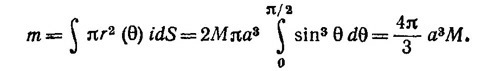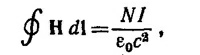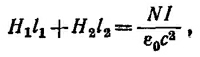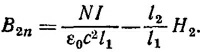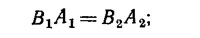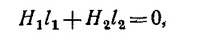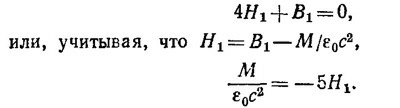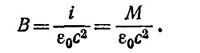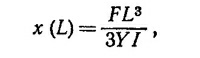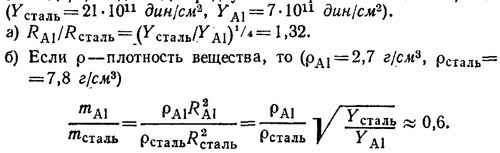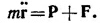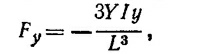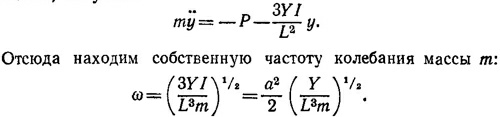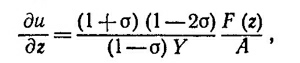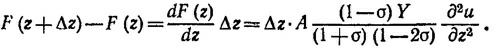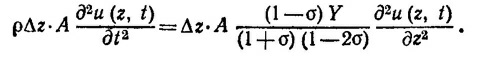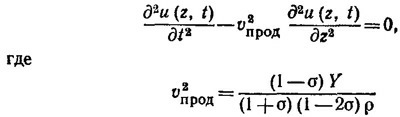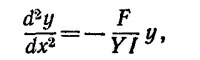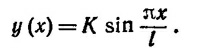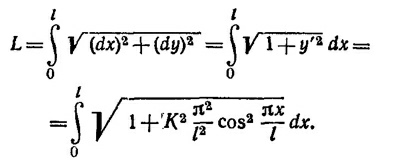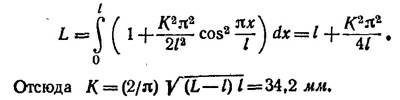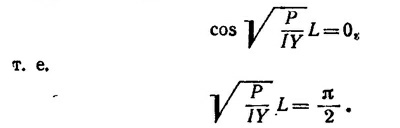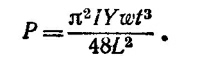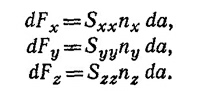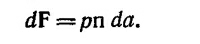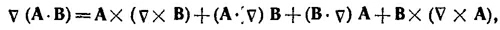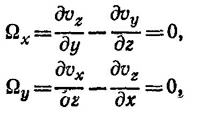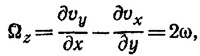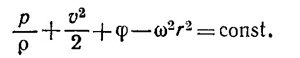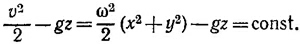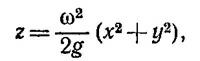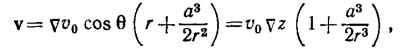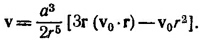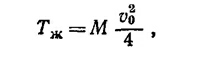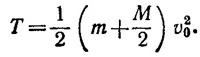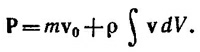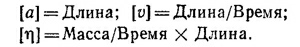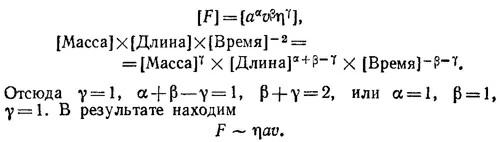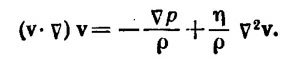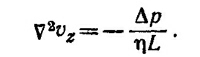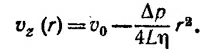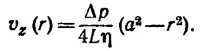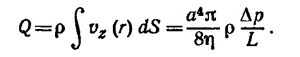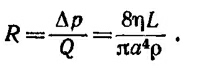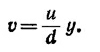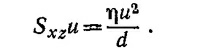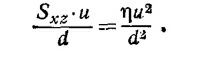| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Продолжение. Решения и ответы к задачам V-VII томов фейнмановских лекций по физике
Следовательно, поток вектора Пойнтинга через поверхность прямолинейного провода равен омическим потерям в этом проводе.
Таким образом, скорость распространения энергии равна
где L = In (b/a)/2πε0c2—емкость единицы длины кабеля (см. решение к задаче 17.6). Заметим, что в cилу того, что LC=1/c2, v=c при R=√L/C.
Тогда мощность, излучаемая антенной, равна среднему по времени потоку вектора Пойнтинга:
В решении к задаче 21.5 отмечалось, что функция cos [(π/2) cosθ]/sinθ хорошо аппроксимируется sinθ. Используя это и учитывая, что cos2ω[t—(r/с)] = 1/2, легко находим W = (2π/3) ε0cα2. Следовательно, α = √3W/2πεос.
б) Используя найденное выражение для α, находим, что максимальные значения напряженностей электрического и магнитного полей равны
27.6. а) Граничные условия заключаются в обращении в нуль тангенциальных составляющих Е на стенках волновода и нормальных составляющих вектора В. Эти условия выполняются, так как Еу(х = 0, а) = 0, Ех(у = 0,b) = 0, Ву(у=0, b)=0 и Вх(х=0, а) = 0.
в) Усредняя выражение для Sz по времени и по сечению волновода, находим
г) Усредняя U по времени и по объему волновода, находим среднюю плотность энергии в волноводе
д) Средняя скорость распространения энергии совпадает с групповой скоростью. Действительно,
[ср. формулу (24.27) «Лекций», вып. 6, стр. 229].
где θ —угол между векторами р и n.
27.8. Считая, что на электрон действует только электрическое поле волны Е = Eо exp (iωt), найдем из уравнения движения mr = qE0 exp (iωt) дипольный момент колеблющегося электрона. Аналогично предыдущей задаче найдем вектор Пойнтинга:
Если ввести угол θ между векторами n и Е, то поток излучаемой энергии в элемент dΩ телесного угла можно записать в виде
Разделив этот поток на плотность энергии в падающей волне J = ε0сE2, получим так называемое дифференциальное сечение рассеяния электромагнитной волны электроном
27.9. Сила светового давления на частицу равна
где S1 —площадь поперечного сечения шарика с радиусом r S0 = 4πR2 (R -расстояние частицы от Солнца); W—энергия, излучаемая Солнцем в единицу времени; β —коэффициент отражения (по условию задачи β = 0). Сила гравитационного притяжения равна
где m — масса частицы, М —масса Солнца (M = 2·1030 кг), G —гравитационная постоянная (G = 6,67·10-8 м3/кг·сек2). В равновесии будут находиться лишь те частицы, радиус которых удовлетворяет условию F1 = F:
здесь ρ —плотность массы частицы. Оценивая радиус частицы в предположении, что ρ ≈ 1 г/см3, находим r0 ≈ 6·10-5 см. Частицы с радиусом r<r0 световым давлением будут отбрасываться Солнцем. Таким образом видно, что обычное объяснение хвостов комет вполне разумно.
Выберем в поперечном сечении тороида контур интегрирования в форме окружности радиусом ρ(0≤ρ≤r). Так как магнитное поле мы считаем однородным по сечению, то магнитный поток через этот контур равен
С другой стороны, считая приближенно напряженность электрического поля одинаковой по величине во всех точках этого контура, интегрируя вдоль него, находим
Энергия, запасенная в тороидальной катушке к моменту времени t, равна
Отсюда полная мощность поглощаемой тороидом энергии, равная потоку вектора Пойнтинга через всю поверхность тороида (последняя приближенно равна 2πrо·2πR), оказывается равной
К главе 28. Электромагнитная масса
Интегрируя по всему пространству в сферической системе координат, находим
28.2. Момент количества движения электромагнитного поля определяется выражением
Подставим выражение для Е и В в формулу для L и проинтегрируем по всему пространству в сферической системе координат. В результате найдем
в) Будем считать, что заряд электрона равномерно «размазан» по поверхности сферы и что сфера вращается с угловой скоростью ω. В этих предположениях задача аналогична задаче 14.6. Если воспользоваться решением к задаче 14.6, положив 4πε0Va = qe, то мы сразу получим искомый результат μ — ωqeа2/3. Отсюда ω=3μ/a2qe. Максимальная скорость электрона на поверхности — это его линейная скорость на экваторе сферы Так как по условию задачи
Следовательно, собственный магнитный момент электрона нельзя объяснить с позиций классической физики — как магнитный момент вращающейся твердой сферы с радиусом, равным электромагнитному радиусу электрона, и с зарядом электрона.
Таким образом, при малых временах v~t, а при t > mc/qE частица движется практически равномерно со скоростью, близкой к скорости света
Переход к движению со скоростью, близкой к скорости света, происходит теперь через время порядка √m2с2+р02/qЕ, т. е. несколько позже. Зависимость х (t) имеет в остальном тот же характер, что и раньше. Что касается зависимости у (t), то при малых временах у ~ t, а при t»√m2с2+р02/qЕ, y~ ln t.
При этом энергия Ε=const, так как F_V. Поскольку E=mc2/√1 — (v2/с2) и р=Ev/с2, то уравнения движения приобретают вид
Умножая второе уравнение на мнимую единицу и складывая его с первым, для комплексной скорости z=vx +ivy получаем уравнение z+¡ωz =0, где частота колебания ω = qBc2/E= (qB/m)√1 —v2/с2. Если протоны движутся медленно, то v2«с2 и циклотронная частота имеет обычный вид ω=qB/m. При увеличении энергии циклотронная частота уменьшится. Так как Δω/ω =—ΔE/E, то при изменении циклотронной частоты на 1% энергия изменится также на 1%.
Из последнего уравнения с учетом начальных условий следует, что z (t)=0. т. е. движение происходит в плоскости ху. Если сложить первые два уравнения, предварительно умножив обе части второго уравнения на мнимую единицу и ввести обозначения ω = qB/m, x+iy =η, то получим одно уравнение η + ¡ωη = iqE/m. Решение этого уравнения будет суммой решения соответствующего однородного уравнения и любого частного решения неоднородного уравнения. Решение однородного уравнения η0 + ¡ωη0 = 0 можно представить в виде η0=С ехр (—iωt), где комплексную константу С можно написать как произведение ее модуля на фазовый множитель: С = а ехр (¡φ). В качестве частного решения неоднородного уравнения можно взять η1 = qEt/mω. Следовательно,
Отделяя мнимую часть от вещественной и принимая во внимание начальные условия, окончательно находим
7
Как указывалось в «Лекциях» (вып. 7, гл. 32, § 3), эти уравнения допускают волновые решения. Будем искать эти решения для волны в виде
Умножая векторно уравнение (в) на k и используя уравнение (б), получаем
Так как электрическая волна поляризована в направлении, перпендикулярном k, то k·Е=0 и D = n2(ω)E, где n2(ω) = c2k2/ω2. Но, с другой стороны, для волны с частотой ω в «линейном» приближении D = ε(ω)E (это приближение справедливо, если электрические поля в диэлектрике слабы по сравнению с электрическими полями в атомах и молекулах; для лазерного луча, направленного на диэлектрик, возникает необходимость учета нелинейной связи D по Е, т. е. учитывать в разложении D по Е члены, квадратичные по Е, кубичные и т. д.). Следовательно, ε(ω) = n2 (ω). Полагая в этом соотношении ω=0 и учитывая, что ε(0) = x, находим
32.2. Квадрат показателя преломления для плазмы в ионосфере имеет вид (см. „Лекции", вып. 7, стр. 67) n2= 1— Nqe2/mε0ω2.
32.3. Так как электрическое поле, действующее на электроны проводимости, равно среднему полю Е, то, полагая ωо = 0 в уравнении (32.1) «Лекций» (вып. 7, стр. 50), vдрейф =х, можно записать уравнение для дрейфовой скорости электронов:
Когда поле Е постоянно действует на электроны проводимости, dvдрейф /dt = 0, для дрейфовой скорости получаем
[см. «Лекции», вып. 7, стр. 68, формула (32.39)].
Это решение отвечает начальному условию задачи, согласно которому vдрейф = v(0)дрейф при t=0. Из него видно, что время, за которое величина дрейфовой скорости уменьшится в e раз, в точности равно τ —среднему времени между соударениями.
то разность фаз, очевидно, равна —π/4.
б) При l = λ2/4 = πс/2n2ω и n22 = n1n3 из системы уравнений, приведенной выше, и из выражения для | а3 |2 следует, что b1 = 0, | а3 |2 = n1/n3, т. е. плотность потока энергии в падающей слева на слой волне |S1|~n1E12 = n1 равна плотности потока энергии прошедшей волны
в) Толщина пленки при этом примерно равна λ/4n2 = 1200Å.
(см. «Лекции», вып. 7, стр. 88).
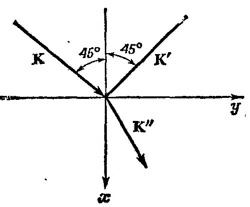
В силу того что х произвольно, из последнего уравнения следует, что sin α = sin β, sin α/sin γ = n2/n1. Отсюда
По условию задачи n1/n2 = 1,6, sin2α=0,5(α=β =45°) и, следовательно, cos γ =√ — 0,28 ≈± ¡0,53. Подставляя найденное значение cos γ в выражение для Е3, получаем (n2 = 1):
К главе 34. Магнетизм вещества
Электрическое поле Е вызвано изменяющимся магнитным полем. Если напряженность электрического поля мала, частица движется приблизительно по окружности, радиус которой равен R =p/qB (p—импульс частицы). Момент количества движения частицы при этом равен J = pR = qBR2. Электрическое поле вызывает изменение абсолютной величины импульса dp/dt = qE, откуда dJ/dt = qER. Величину Е можно вычислить, пользуясь теоремой Стокса:
Наши рассуждения годятся только в том случае, если частица движется по круговой орбите, т. е. если Т (dJ/dt) = (T/2) (dB/dt) «1, где T —период обращения частицы по орбите.
Частота ядерного магнитного резонанса равна (см. «Лекции», вып. 7, § 6, стр. 130)
где vр = ωр/2π. Подставляя численные значения для vp и T, данные в условии к задаче, находим g = 5,46.
Предполагая, что магнитное поле мало, так что μВ/kT «1, разложим экспоненту в ряд и ограничимся первыми двумя основными членами разложения:
Интегрируя это выражение по всем телесным углам, получаем N —полное число моментов, N = 4πn0. Полный магнитный момент определим следующим образом (k —единичный вектор в направлении В):
Подобная теория классического парамагнетизма не противоречит утверждению о том, что в рамках классической физики парамагнетизм вообще отсутствует. Просто классическая физика не может обосновать существование у каждого атома «собственного» магнитного момента μ. Наличие его есть чисто квантовый эффект.
При T = 300°К отношение μ0В/kТ равно 2,3·10–3 и, следовательно, Nизб/N = th0,0023≈ 0,23%. При T = 4,2°К отношение μ0В/kТ равно 0,16 и Nизб/N=15,9%.
то энергии, соответствующие различным проекциям спина в магнитном поле, равны U= —μ0В для Jz/h= +1, U =0 для Jz/h=0 и U=+μ0В для Jz/h =–1. Согласно статистической механике,
Постоянная находится из условия равенства числа частиц с разными проекциями полному числу частиц N:
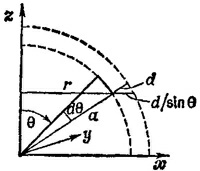
Так как ось у направлена по касательной к поверхности шара, то ∂М/∂у = 0. Далее, Δx = d/sin θ; стало быть
Это соотношение можно также записать в виде i =M x n где n —нормаль к поверхности шара.
36.2. Из теоремы Стокса (в качестве контура выберем среднюю линию магнита) следует
где N —полное число витков обмотки; I —сила тока в обмотке. Разделяя контурный интеграл на две части, одна из которых отвечает зазору, а другая —контуру вне его, и предполагая, что поле Н по всему периметру средней линии ярма однородно, в результате интегрирования находим
где H1 — поле в зазоре; H2 —поле в каркасе магнита; l1=1 см—ширина зазора; l2 = 375 см —периметр средней линии. Граничные условия в зазоре имеют вид B1n = B2n, причем В1n = H1. Выражая Н1 через В2n, находим уравнение
Построив эту прямую на графике B2n = f(H2) (см. стр. 386), можно найти H2 и В2n. Тогда поле в зазоре равно H1 = B2n (для указанных параметров магнита эта линейная зависимость имеет вид В2n = 1,35 вебер/м2—375H2). Согласно графику, H1 = В2n= 1,17 вебер/м2.
здесь A1 = 100 см2—площадь поперечного сечения магнита; A2 = 20 см2 — площадь зазора. Отсюда В2 = 5В1. После выключения тока циркуляция магнитной индукции H по средней линии системы будет равна нулю. Считая поле магнитной индукции в магните однородным и учитывая, что магнитная восприимчивость мягкого железа бесконечна, т. е. в мягком железе H=0, запишем
где l1 = 20 см—длина постоянного магнита; l2=1 см—ширина зазора. Так как в зазоре H2 = В2 = 5B1, из последнего уравнения находим
Если эту прямую линию построить на приведенной в условии задачи кривой М—H (стр. 387), то она пересекает ее в двух точках, отвечающих H1=±0,04 вебер/м2. Так как при уменьшении тока система окажется на верхней части кривой М—H, то Н1=—0,04 вебер/м2. Тогда В1=—4H1=0,16 вебер/м2 и искомая напряженность магнитного поля, т. е. В2 = 5В1 = 0,8 вебер/м2.
Направление поля Н совпадает с направлением вектора В. Так как Н = В–М/ε0c2, то внутри стержня H = 0.
где Y — модуль Юнга, I—момент инерции сечения стержня. По определению, жесткость равна отношению F/x(L) =3YI/L3. По условию задачи алюминиевый и стальной стержни обладают одинаковой жесткостью и имеют одинаковую длину. Следовательно, YА1IА1 = YстальIсталь. Так как момент инерции круглого сечения стержня равен I = πR4/4, где R—радиус поперечного сечения, то
38.2. На тело m действуют две силы: вес тела Р и упругая сила F со стороны стержня, действующая в вертикальном направлении. Поэтому уравнение движения этого тела запишется в виде
Спроектируем это уравнение на вертикальную ось (ось у): my = Fy –P. Согласно формуле для отклонения конца стержня, жестко заделанного в стенку, сила, с которой незакрепленный конец стержня действует на тело m, равна
где у —вертикальное смещение массы m; Y —модуль Юнга; I —главный момент инерции сечения стержня: / I= а4/12. Подставляя это выражение для силы Fy в уравнение движения, получаем
38.3. Рассмотрим массивное тело, поперечные размеры которого много больше длины волны звука. Ударяя по такому телу, можно обнаружить, что оно не раздается во все стороны, а сжимается только в направлении удара. В таком теле побежит продольная волна, в которой частицы тела движутся только в направлении распространения волны. Чтобы найти уравнения, описывающие распространение такого продольного звука, мы фактически можем рассмотреть стержень, который закреплен так, что при сжатии и растяжении его боковые размеры не сокращаются. Пусть площадь поперечного сечения такого стержня равна А, а длина L. Рассмотрим элемент стержня длиной Δz, расположенный на расстоянии z от его конца. Обозначим через u (z, t) смещение этого элемента в волне в момент времени t. При статическом растяжении (или сжатии) внутреннее напряжение F/A на всем протяжении стержня одно и то же и пропорционально u/L, где u — удлинение стержня. В упругой волне важна местная деформация в точке z, т. е. ∂и (z, t)/∂z. Для стержня без бокового смещения (см. «Лекции», вып. 7, стр. 196) было найдено
где F (z) —сила, действующая в поперечном сечении на расстоянии z от начала координат. На одном конце элемента Δz действует F (z), а на другом F(z+Δz). Полная сила, действующая на элемент Δz, очевидно, равна
Согласно закону Ньютона, эта сила равна произведению массы элемента ρΔz·A (ρ —плотность тела) на его ускорение ∂2u (z, t)/∂t2:
Сокращая обе части получившегося уравнения на Δz·А, получаем
—квадрат фазовой скорости распространения продольных волн в твердом теле.
где Y —модуль Юнга; I —момент инерции поперечного сечения линейки. Из этого уравнения следует:
Постоянную К можно определить из условия нормировки на длину линейки
Учитывая тот факт, что прогиб линейки слабый, т. е. что К/l «1, вычислим интеграл, разложив подынтегральное выражение в ряд
б) Сила, с которой линейка упирается в планки, равна F= π2YI/l2, где I=аb3/12. Если принять для стали Y = 2·1012 дин/см2, то F = 1,47 кГ.
где А и В — константы. Из граничного условия θ(0) = 0 (нижний конец стержня жестко заделан) находим В=0. Из условия равенства нулю момента сил внутренних напряжений у свободного конца, т. е. из граничного условия θ’ (L)=0, находим
Следовательно, P = π2IY/4L2. Учитывая, что I=wt3/12, окончательно находим искомую силу
К главе 40. Течение «сухой» воды
Поскольку проекция силы dF на площадку da должна быть равна нулю (отсутствуют касательные напряжения), то это означает, что вектор dF должен быть направлен вдоль n. Это может быть только при условии, что диагональные элементы тензора S¡j равны друг другу, т. е. если Sxx=Syy=Szz = p. Отсюда
Следовательно, какое бы направление вектора n мы ни выбрали, всегда сила, действующая на единичную площадку, перпендикулярную этому направлению, нормальна к площадке и равна численно одному и тому же значению р (давление).
если положить в нем A = B = v.
или в векторном виде Ω=2ω. Отсюда ясно, что в данной задаче Ωxv = — 2ω2r. Так как можно представить r = V (r2/2), то во всех точках жидкости выполняется уравнение
Так как на поверхности жидкости давление постоянно и равно атмосферному, то имеем (φ=gz)
В нашей системе координат, очевидно, const =0. Поэтому уравнение поверхности жидкости имеет вид
т. е. поверхность является параболоидом вращения.
где v0 —скорость воды на бесконечном расстоянии от шара, θ —угол между радиусом-вектором r и v0 (ось z выбрана вдоль вектора v0). В настоящей задаче мы можем воспользоваться этим решением, если перейдем к системе координат, в которой жидкость вдалеке от шара покоится. Результат можно записать в виде
Кинетическая энергия жидкости Тж равна интегралу от квадрата этой скорости, умноженному на плотность жидкости, по всему пространству вне шара. Математически, как мы видим, задача аналогична задаче 27.2, где определялась энергия магнитного поля Земли. Воспользовавшись найденным в этой задаче результатом, получим
где М —масса жидкости в объеме шара. Добавляя к Тж кинетическую энергию шара, находим полную энергию
Полный импульс системы вычисляется по формуле
Подставляя в нее приведенное выше поле скоростей v и выполняя несложное интегрирование, получаем ∫ρv dV = 0; следовательно, P = mv0.
Будем искать из соображений размерности выражение для силы в виде F = aαvβvγ. Запишем условие совпадения размерностей левой и правой частей этого соотношения:
To, что параметры входят в выражение для F так, как было найдено выше, а не иначе, ясно из следующих качественных соображений. В «Лекциях» (вып. 7, стр. 260) указывалось, что вязкая сила fвязк, действующая на единицу объема жидкости, пропорциональна коэффициенту вязкости η и вторым производным скорости по координатам. Так как в задаче о движении шара в вязкой жидкости характерным размером, на котором существенно меняется скорость, являются размеры порядка размеров шара, то вторые производные по порядку величины равны v/а2. Умножая fвязк на объем, где силы вязкости отличны от нуля, т. е. на объем порядка а3, находим F ~ ηav. Заметим, что сила трения, действующая на гармонический осциллятор, также пропорциональна скорости осциллятора.
Так как в данной задаче отлична от нуля лишь z-компонента скорости –vz, причем vz зависит только от r —расстояния от оси трубы, то (v·V)v = 0. Записав Vp =–Δр/L, где Δр=p1–р2 —разность давлений на концах трубы, получим
Это уравнение совпадает по виду с уравнением Пауссона для потенциала равномерно заряженного бесконечного цилиндра V2φ =— ρ/ε. Потенциал φ легко найти, если воспользоваться теоремой Гаусса, найти напряженность электрического поля, а затем проинтегрировать соотношение Е=—Vφ. В результате φ = φ0—ρr2/4ε0, где φ0 —постоянная интегрирования. Заменяя φ на vz и ρ/ε0 на Δp/ηL, получаем
Неизвестную константу v0 легко найти, если вспомнить, что на стенке трубы скорость жидкости равна нулю. Окончательно:
Поток массы жидкости плотности ρ через поперечное сечение (расход) трубки равен
Если провести аналогию между разностью потенциалов и разностью давлений, а также расходом жидкости и электрическим током, то под сопротивлением трубы надо понимать величину
Аналогом конденсатора являются два сообщающихся сосуда, снизу соединенные трубкой, которую можно перекрывать краном так, что уровень воды в сосудах может быть разным.
б) Силу трения, действующую на единицу поверхности доски, найдем, исходя из формулы Sxz=η(dv/dy)=ηu/d, где η —коэффициент вязкости. При этом работа на преодоление силы трения, совершаемая в единицу времени и отнесенная к единице площади поверхности доски, равна
Искомая же скорость диссипации энергии в единице объема оказывается равной
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

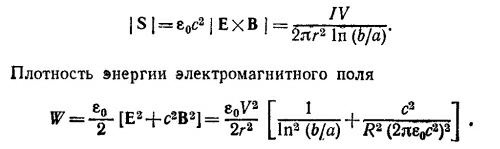
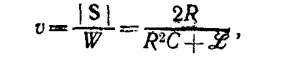

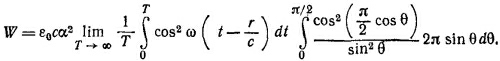
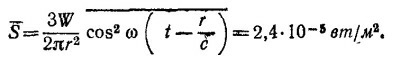
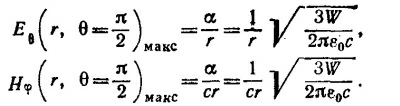
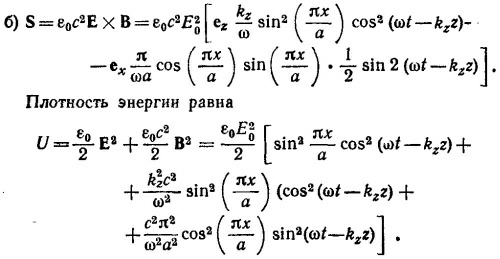
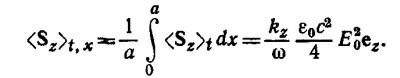
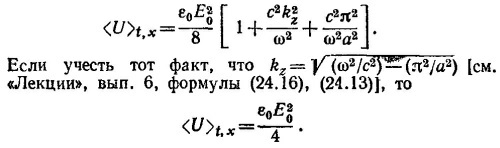
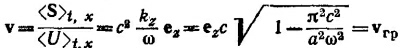
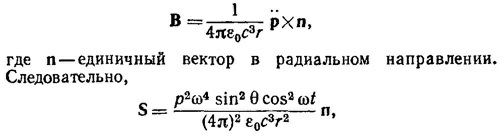
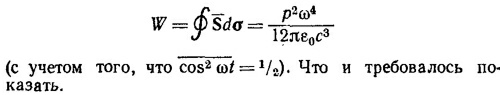
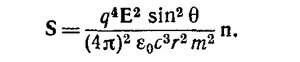
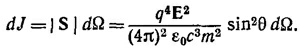
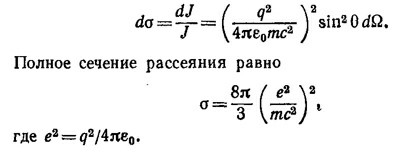
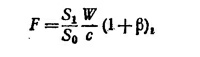
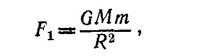
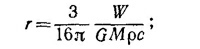
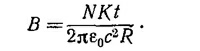
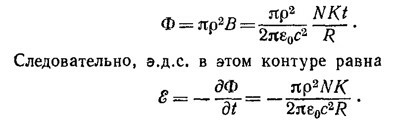
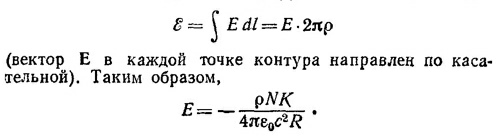
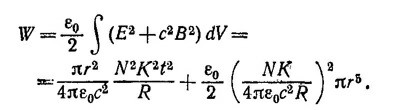
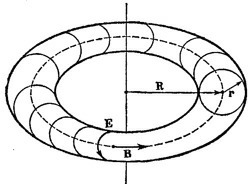 б) Найдем направление и величину вектора Пойнтинга на поверхности тороида. Величины напряженности E и В найдены в пункте (а). Направления Е и В таковы, что вектор Пойнтинга S в каждой точке на поверхности тороида нормален к поверхности и направлен внутрь тороида. Кроме того, E_B в каждой точке. Следовательно, модуль вектора Пойнтинга равен
б) Найдем направление и величину вектора Пойнтинга на поверхности тороида. Величины напряженности E и В найдены в пункте (а). Направления Е и В таковы, что вектор Пойнтинга S в каждой точке на поверхности тороида нормален к поверхности и направлен внутрь тороида. Кроме того, E_B в каждой точке. Следовательно, модуль вектора Пойнтинга равен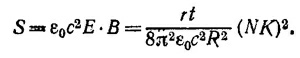
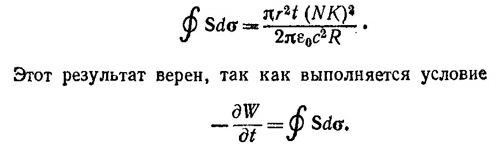
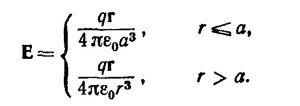

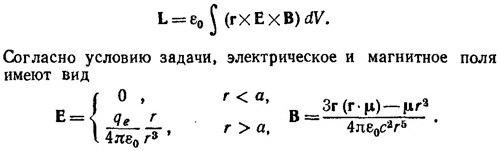
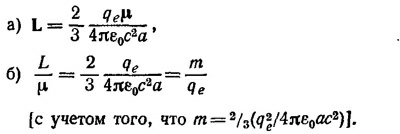
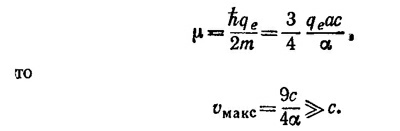
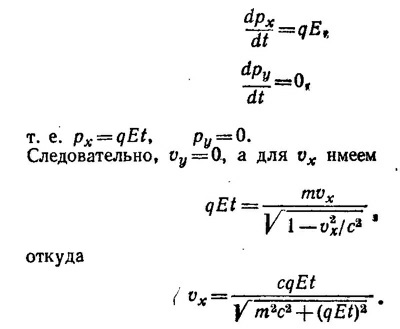
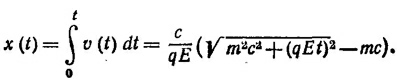

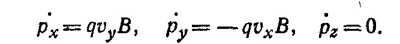
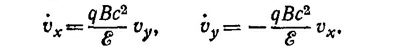
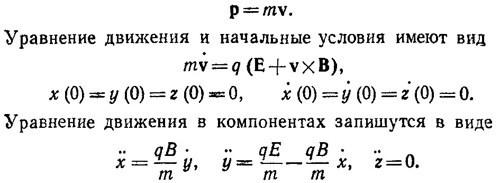
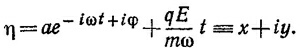
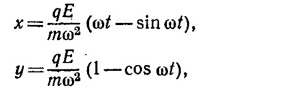
 т. е. траектория в плоскости является циклоидой (см. рисунок).3аметим, что из выражения x = (qE/mω)(1 — cos ωt) следует, что предположение о нерелятивистском характере движения справедливо, если qE/mω«c, т. е. Е/Вс«1.
т. е. траектория в плоскости является циклоидой (см. рисунок).3аметим, что из выражения x = (qE/mω)(1 — cos ωt) следует, что предположение о нерелятивистском характере движения справедливо, если qE/mω«c, т. е. Е/Вс«1.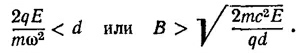
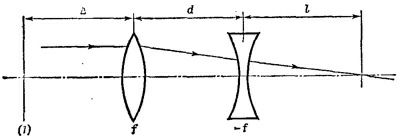 29.4. Для данной системы двух тонких линз существует соотношение F-1 = f-1 + (—f)-1—d (f)-1 (—f)-1, где F —фокусное расстояние системы, отсчитываемое от главных плоскостей системы.
29.4. Для данной системы двух тонких линз существует соотношение F-1 = f-1 + (—f)-1—d (f)-1 (—f)-1, где F —фокусное расстояние системы, отсчитываемое от главных плоскостей системы.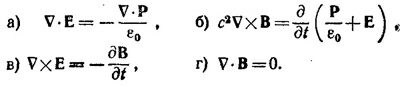
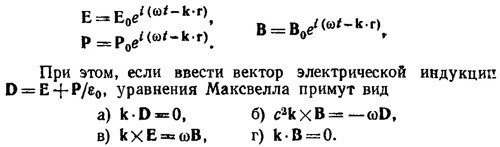
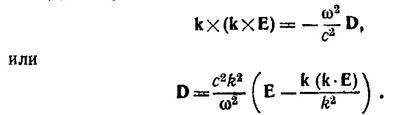
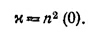
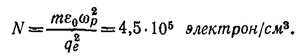
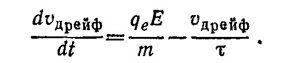
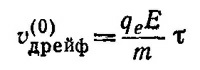
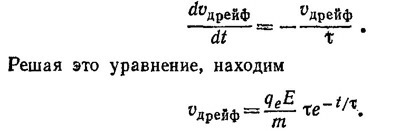
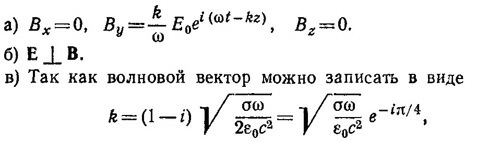
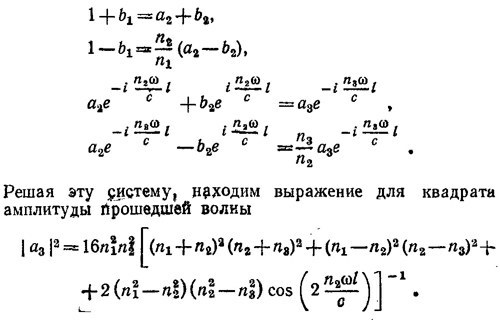
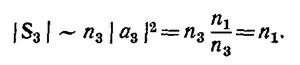
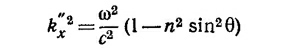
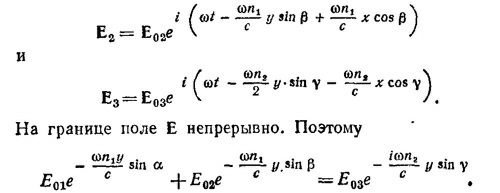
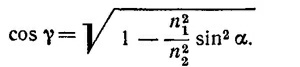
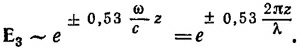
 Верхнему знаку отвечает экспоненциально нарастающее поле, нижнему—убывающее. Оставляя из физических соображений последнее решение, находим, что в воздухе за большой гранью призмы электрическое поле волны убывает в е раз на расстоянии x = 0,Зλ= 1350 Å. Если вектор Е лежит в плоскости падения, результат будет точно таким же.
Верхнему знаку отвечает экспоненциально нарастающее поле, нижнему—убывающее. Оставляя из физических соображений последнее решение, находим, что в воздухе за большой гранью призмы электрическое поле волны убывает в е раз на расстоянии x = 0,Зλ= 1350 Å. Если вектор Е лежит в плоскости падения, результат будет точно таким же.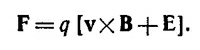
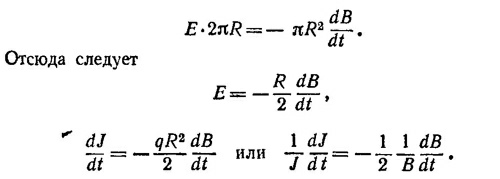
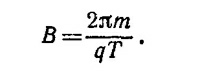
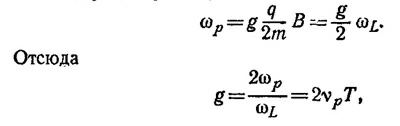
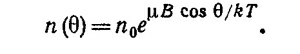
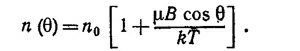
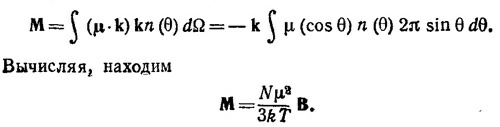
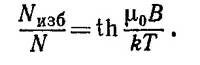
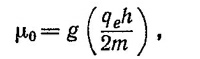
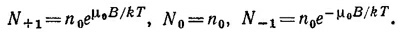
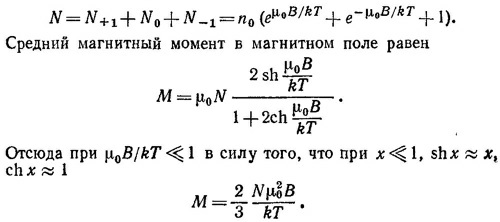
 К главе 36. Ферромагнетизм
К главе 36. Ферромагнетизм