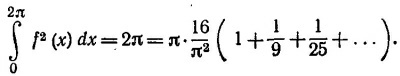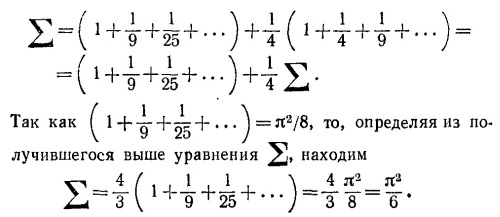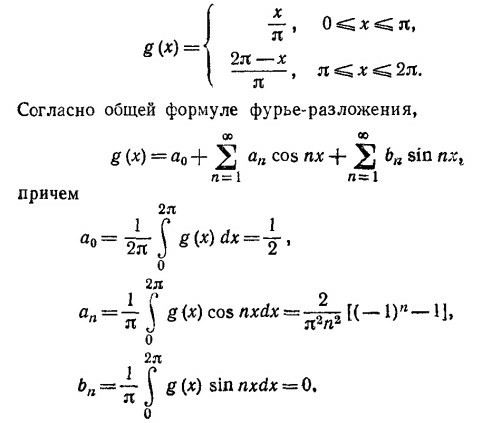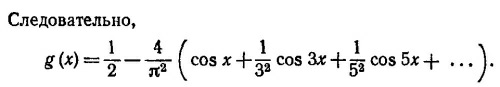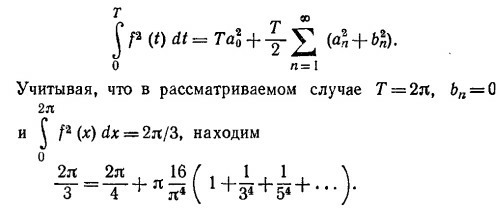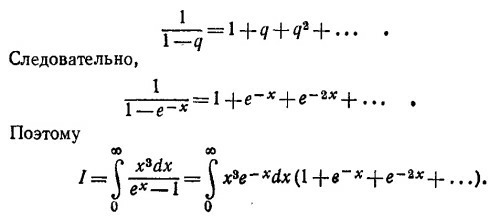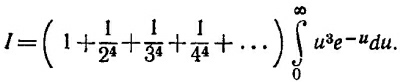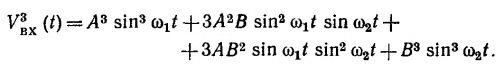| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Продолжение (начиная с 20.6). Решения и ответы к задачам I-IV томов фейнмановских лекций по физике
Линейные скорости центров масс стержней O1 и O2, возникающие за счет вращательного движения, равны по модулю
и направлены перпендикулярно линии O1O2. В системе координат, изображенной на рисунке, скорость поступательного движения имеет только х-составляющую, а вращательные скорости точек О1 и O2 образуют угол 45° с осями координат. Результирующие скорости центров масс стержней v1 и v2 равны векторной сумме скорости центра масс системы в целом и скорости, приобретенной центрами масс стержней за счет вращательного движения. Имеем
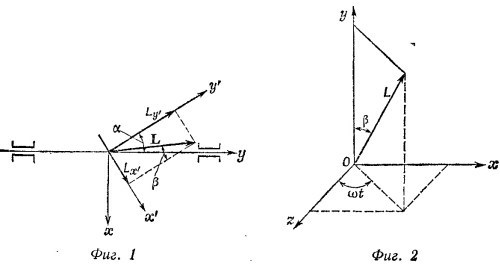
20.7. Направим ось у вдоль вектора угловой скорости маховика (т. е. по оси вращения). Введем также другую систему координат х’у’, ось у’ которой перпендикулярна плоскости диска, а х’ лежит в этой плоскости. Компоненты угловой скорости в этой системе
(α — угол между осью вращения и осью у’). Компоненты момента количества движения в штрихованной системе координат равны
(M —масса диска, R —его радиус).
Так как углы α и β малы, можно положить tg (α– β) ≈ α– β, a tg α ≈α, так что α– β = 1/2 α откуда β = 1/2 α. В нештрихованной системе координат вектор количества движения L вращается вокруг оси у с угловой скоростью
ω. Следовательно, его х- и z-компоненты меняются со временем по закону (фиг.2)
20.8. Силы притяжения тел массы m к массе M равны
20.9. Сплюснутость Земли при вычислении действующего на нее момента сил можно приближенно учесть, заменив Землю двумя точечными массами, находящимися на некотором расстоянии друг от друга. Далее, воспользовавшись конечным результатом предыдущей задачи, находим отношение вращательных моментов, создаваемых Солнцем и Луной:
где МЛ и МС —массы Луны и Солнца, а RЛ и RС — расстояние от Земли до Луны и Солнца соответственно.
Полный момент инерции Земли равен сумме моментов инерции шаровых слоев, так что
б) Момент количества движения Земли L равен
(t = 8,64·103 сек— период обращения Земли вокруг своей оси).
20.11. 1) Согласно формуле, полученной в задаче 10.8. (стр. 164), кинетическая энергия катящегося тела складывается из кинетической энергии движения его центра масс и кинетической энергии тела в системе ц. м. Так как тело скатывается по наклонной плоскости без скольжения и ввиду симметрии тела относительно оси вращения, его центр масс находится на этой оси, движение тела в системе ц. м. представляет собой чистое вращение, угловая скорость которого ω = v/r (v—скорость тела в произвольный момент времени). Таким образом, кинетическая энергия тела
где / — момент инерции тела относительно оси вращения. Величину скорости v центра масс в нижней точке наклонной плоскости определим из закона сохранения энергии
2) Применим эту формулу для частных случаев, перечисленных в условии задачи.
20.12. а) Центр масс однородного стержня находится в его середине, т. е. на расстоянии L/2 от конца. Центр масс системы из стержня и замазки находится посредине отрезка, соединяющего замазку и точку О, т. е. на расстоянии L/4 от линии удара.
Из закона сохранения импульса следует, что скорость центра масс после удара не изменилась, т. е. осталась равной v/2.
а ω —угловая скорость вращения относительно центра масс.
г) Так как скорость центра масс равна v/2, кинетическая энергия системы после удара
(Tн = 1/2Мv2 — начальная кинетическая энергия системы).
(ω и ω+Δω —угловые скорости вращения Земли в два рассматриваемых момента), или
Учитывая, что для воды ρ=1 г/см3 = 103 кг/м3, а период вращения Земли T = 24 час, получаем ΔT ˜1 сек.
Скорость точки А в момент удара есть сумма скоростей двух движений: поступательного со скоростью v0 и вращательного с угловой скоростью ω. Поэтому
К главе 21. Гармонический осциллятор
Но ω = dθ/dt, поэтому после дифференцирования по времени получим
Это и есть дифференциальное уравнение, описывающее изменение угла θ со временем.
В § 2 гл. 21 «Лекций» (вып. 2, стр. 48) было показано, что такое дифференциальное уравнение описывает колебания с периодом Т = 2π/ω, где ω2 = Mgd/I Поэтому период малых колебаний тела
21.2. В найденном в предыдущей задаче выражении для периода колебаний положим I =IC+Мd2. Тогда
а) Найдем d, соответствующее данному значению периода. Решая квадратное уравнение
в) Период минимален при таком значении d, при котором минимально выражение
(подкоренное выражение в формуле для периода). Условие минимума имеет вид
Подставляя это выражение в формулу для периода колебаний, получаем минимальное значение периода
Поместим начало координат в точку l0, а ось х направим вертикально вниз. В этом случае уравнение движения грузиков примет вид
Как известно, дифференциальное уравнение такого типа описывает колебания с периодом
Легко убедиться в том, что решением этого уравнения является функция
где B1 и B2 —постоянные, определяемые из начальных условий. Систему координат мы выбрали таким образом, что х = x0 =—А при t= 0. Начальную скорость v0 находим, учитывая сохранение импульса при ударе
Этим начальным условиям соответствуют постоянные B2=—В1 =А, т.е. решение уравнения движения имеет вид
Амплитуда колебаний, т. е. максимальное отклонение точки от положения равновесия, достигается в тот момент времени t1, когда скорость колеблющихся грузов равна нулю:
Максимальная высота подъема над первоначальным положением равновесия (находящимся на расстоянии А вверх от начала координат)
21.4. а) Частицы А и В движутся вдоль прямой по закону
21.5. В задаче 21.1 получено уравнение малых колебаний твердого тела
где d —расстояние от оси вращения до центра масс тела, I —момент инерции тела относительно оси, проходящей через точку подвеса. Из него следует, что
Если масса единицы длины проволоки ρ, то масса всего каркаса М = ρ (πR+2R) = ρR (π+ 2) (R — радиус полуокружности АСВ), а
Центр масс полуокружности АСВ лежит на перпендикуляре к диаметру АВ, проходящем через точку подвеса Р на расстоянии (см. задачу 19.13.)
21.6. Обозначим жесткость пружины через k. Период колебания пластинки массы m и грузика массы m1 равен
Удлинение пружины после того, как с пластинки снят груз m1 и положен груз m2:
21.7. После удара центр масс всей системы будет двигаться вправо со скоростью vц.м. , определяемой из закона сохранения количества движения:
В системе координат, жестко связанной с центром масс системы, частицы (массой M каждая) совершают гармонические колебания (при этом они движутся либо навстречу друг другу, либо в противоположные стороны) около положений равновесия, лежащих в точках —L/2 и L/2 для левой и правой массы соответственно.
Вычитая из второго уравнения первое, получаем
где ω = 2π√M/k, а A1 и A2 определяются начальными условиями. В момент столкновения пружина была ненапряжена, т. е. х = 0, а массы двигались навстречу друг другу со скоростями 1/8v, т. е. x = 1/4v. При таких начальных условиях A1 = 0, B1 = v/4ω, т. е. x= (v/4ω) sin ωt. Итак, период колебаний системы равен
21.8. Из условия задачи следует, что действующая на частицу сила прямо пропорциональна r — расстоянию от центра Земли и направлена к центру, поэтому mr+kr = 0, где k — коэффициент пропорциональности в зависимости силы от расстояния. Таким образом, частица совершает колебания вокруг центра Земли с периодом
где ω2 = k/m.
21.9. Обозначим через n число бактерий в колонии. Скорость роста населения колонии равна dn/dt. По условию
Это и есть дифференциальное уравнение роста колонии. Из него следует, что население колонии растет со временем по закону n=n0eαt.
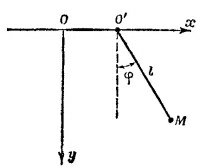
Предположим, что φ мало, так что sin φ≈ φ, cos φ=1. В этом приближении (приближении малых колебаний) уравнение для φ имеет вид
Мы пришли к такому же дифференциальному уравнению для хм, как и в § 5 гл. 21 «Лекций» (вып. 2, стр. 105), только в правой части вместо функции cos ωt имеем sin ωt. Поэтому будем искать решение в виде хм = с sin ωt (с—амплитуда колебаний).
К главе 22. Алгебра
Приравнивая по отдельности в этом соотношении вещественные и мнимые части, получаем требуемую формулу.
б) В результате перемножения получается вектор в комплексной плоскости, длина которого равна произведению модулей, т. е. А·В, а его направление составляет угол θ + Ф с вещественной осью.
К главе 23. Резонанс
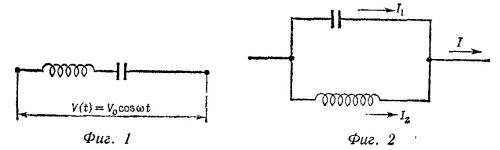
23.2. а) Рассмотрим цепь, изображенную на фиг. 1. Введем комплексное напряжение ˆV=V0еiωt и комплексный заряд ˆq (t) на обкладках конденсатора. Тогда на основании решения к задаче 23.1 напишем дифференциальное уравнение для определения стационарного тока
где I= dq/dt.
Будем искать решение этого уравнения в виде I =Îеiωt. Выполнив необходимое дифференцирование, мы найдем связь между Î и ˆV
Отсюда следует, что импеданс цепи ˆZ =ˆV/Î в случае последовательного соединения равен
б) При параллельном соединении емкости и индуктивности электрическая цепь имеет вид, изображенный на фиг. 2. В этом случае, очевидно, выполняется условие равенства потенциалов на индуктивности и емкости
где Î2 — комплексный ток через индуктивность. Суммарный ток через цепь равен Ι= Ι1 + Ι2. где Ι1— ток через емкость. Учитывая тот факт, что
При последовательном соединении при ω →∞ сопротивление цепи обусловлено индуктивностью, а при ω →0 —емкостью. При частоте ω =1/√LC имеет место «резонанс»: импеданс цепи обращается в нуль.
Поделим обе части этого уравнения на массу m и перенесем все члены уравнения в левую часть, затем, используя обозначение ω02= k/m, получим искомое уравнение,
(Здесь учтено, что γ< 2ω0.) С учетом найденного запишем общее решение уравнения движения:
где С1 и D1 — комплексные постоянные интегрирования. Представляя эти постоянные в виде С1 = Сеiθ1 и D1=Deiθ2, где С и D—вещественные числа, и определяя вещественную часть х, находим
Воспользовавшись формулой для косинуса суммы углов найдем, что решение можно представить в искомом виде, если вместо произвольных постоянных С, D, θ1 и θ2 ввести новые две вещественные постоянные А и В, связанные с ними соотношениями в) В этом случае α1 и α2 — вещественны и общее решение уравнения движения имеет вид
23.4. Следует рассмотреть два случая:
23.5. Обозначим через Î1 и Î 2 — комплексные токи, протекающие через точки А и B. Тогда, очевидно,
Таким образом, найденное выражение для разности потенциалов ˆVАB можно представить в виде произведения модуля комплексного числа, равного V/2, на фазовый множитель. Фаза разности потенциалов ˆVАB при этом равна
Так как при изменении х от 0 до ∞ функция arc tg x меняется в пределах от 0 до π/2, то, меняя R’ (в пределах от 0 до ∞), можно менять фазу ˆVAB от π до 0.
Отсюда следует, что должно выполняться соотношение
б) Определяя вещественную часть найденных выражений для ÎA и ÎB находим
К главе 24. Переходные решения
Если искать решение этого уравнения в виде x = Aeαt, то легко найти, что α1=0, α2=—γ. Следовательно, общее решение этого уравнения можно представить так:
24.2. Для заряда q (t) на обкладках конденсатора можно написать следующее дифференциальное уравнение:
Так как напряжение на конденсаторе связано с зарядом соотношением q(t)/C = V (t), то можно написать
Решение этого уравнения, удовлетворяющее заданному начальному условию V (0) = V0, имеет вид
24.3. Уравнение движения тела вдоль оси x можно записать в виде
а) В установившемся движении скорость тела будет постоянна, т.е. dv/dt =0. Отсюда
б) Попытаемся найти решение неоднородного уравнения
в виде суммы решения однородного уравнения v+γv=0 и любого решения неоднородиого уравнения. В качестве последнего можно выбрать
Так как общее решение однородного уравнения имеет вид v = Ae–γt, где А — произвольная константа, то
Непосредствеиной проверкой мы убеждаемся, что получили самое общее решение исходного уравнения.
24.4. Для мгновенного значения заряда на обкладках конденсатора можно написать следующей дифференциальное уравнение:
Обозначим ω2=1/LC. Тогда написанное выше уравнение приобретает вид уравнения гармонического колебания: q+ω2q = 0. Общее решение этого уравнения имеет вид
Начальное условие состоит в том, что V0 = q(0)/C при t = 0 и ток в начальный момент времени равен нулю, т. е. dq/dt=0. Определяя из этих условий константы А и В, находим
а) Тан как в каждый момент времени напряжение на конденсаторе равно V (t) = q (t)/C, то
б) Используя этот результат, находим, что запасенная в конденсаторе электростатическая энергия, равная CV2/2, и энергия магнитного поля в катушке LI2/2 изменяются со временем по закону
Сумма названных выше энергий, как нетрудно видеть, равна энергии 1/2CV02 первоначально запасенной в конденсаторе.
Так как, согласно решению задачи 24.4, мгновенное значение заряда на обкладках конденсатора можно представить в виде
где ω=1/√LC, то с учетом начальных условий находим напряжение на конденсаторе в момент времени V (t) = q (t)/C:
Из этого выражения видно, что максимальное напряжение на конденсаторе (амплитуда напряжения) равно
24.6. а) Уравнение движения тела до включения замедлителя в буквенных обозначениях имеет вид
После включения замедлителя уравнение движения имеет другой вид:
Общее решение последнего уравнения найдено в гл. 24 «Лекций» (вып. 2). Как следует из этого решения, амплитуда колебаний тела уменьшается со временем по закону ехр( —γt/2), причем новый период колебания равен
по условию задачи амплитуда колебания уменьшается в два раза, т. е. справедливо соотношение 1/2 = e-γt0/2. Отсюда находим
в) Если амплитуда уменьшается в 4 раза, то ехр (— γt1/2) = 1/4,т.е. t1 ≈4 In 2/γ ≈ 20 сек. Так как период колебания равен Т ≈ T0 = 1 сек, то уменьшение амплитуды колебания в 4 раза произойдет за 20 полных колебаний, а в 10 раз примерно за 33 или 34 полных колебания.
Здесь мы учли, что γ«ω0. Нисколько не уменьшая общности вывода, предположим, что в момент включения затухания, т. е. при t = t0 тело двигалось таким образом, что А = 0 (ведь начальное состояние тела в условии задачи не фиксировано!). Отсюда
Из этого выражения видно, что скорость диссипации энергии была максимальна при t=t0. В этот момент времени она была равна γmω02B2. Согласно условию задачи, В = 0,2 м, γ = 0,693, m= 5, ω02=4π2. Отсюда находим P= 1,1 вm.
а) Так как при t≤0 сила на осциллятор не действовала, то в начальной момент времени он покоился (ведь осциллятор с затуханием!). Общим решением уравнения движения при t > 0 (действующая сила постоянна!) является решение
Мы предполагали выше, что ω02 > γ2/4, В противном случае, когда ω02 < γ2/4, и, следовательно,
где A и В — постоянные интегрирования, которые надлежит определить из начальных условий х (0) = 0 и ·x (0) = Jx/m. В результате находим
в) Найдем вначале частное решение уравнения движения. Будем искать его в виде х1 (t) = D sin ω0 t. Подставив это выражение в уравнение движения, определим константу D
2) Будем искать частное решение неоднородного уравнения движения в виде х1 (t) = C cos ωt+D sin ωt. Подставляя это выражение в исходное уравнение и приравнивая отдельные коэффициенты при cos ωt и sin ωt, находим
За достаточно большое время t»2/γ решение, отвечающее собственным затухающим колебаниям, обратится в нуль, а основными останутся лишь вынужденные колебания. Амплитуда последних резонансно зависит от частоты, из приведенного выражения видно, что наибольшей амплитудой обладают колебания с частотой ω*= √ω02—γ2/2. При этом амплитуда «резонансного» колебания равна F0/mγ√ω02—γ2/4.
где ω=120 сек–1. Дифференциальное уравнение, описывающее напряжение на конденсаторе, т. е. Vвых (t), имеет вид
Решение соответствующего однородного уравнения легко найти. Оно имеет вид
Эта часть решения существенна лишь в начальные моменты времени работы выпрямительного устройства. Она за времена, большие чем RC, экспоненциально быстро обратится в нуль, и ее можно в дальнейшем игнорировать.
Подставляя V(1)вых в исходное дифференциальное уравнение и по отдельности приравнивая коэффициенты при cos ωt и sin ωt в правой и левой частях уравнения, находим
Из этого выражения видно, что постоянная составляющая напряжения остается той же, но амплитуда переменной составляющей равна
Подставляя в это выражение R = 103 ом, С = 10 мкф, ω=2π·120 сек–1, находим V′2 = V2/7,6, т. е. амплитуда переменной составляющей уменьшается в 7,6 раза.
Так как, согласно схеме цепи, Vвх =V1+Vвых, то
Если |Vвых|«|Vвх|, то получим Vвых(t)=СR(dVвх/dt).
Из этого выражения видно, что условие | Vвых | « | Vвх |, фигурирующее в предыдущей задаче, сводится к условию СRω«1, т. е. T»1/CR. Следовательно, уже за время, меньшее одного периода колебаний, первый член в выражении для Vвых станет пренебрежимо малым и выходное напряжение можно представить в виде
25.4. Простейшей цепью, с помощью которой можно было бы интегрировать входную функцию, является цепь, изображенная на рисунке в условии к задаче 25.2 (стр. 77), но в которой Vвх и Vвыx поменялись местами. В этом случае, используя результат задачи 25.2, можно записать
25.5. а) На тело, сдвинутое на расстояние х от центральной точки, действуют две упругие силы: со стороны правой пружины сила, равная –kx/2, и со стороны левой — сила, равная –kx/2. Суммарная упругая сила, таким образом, равна –kx. В предположении о постоянстве коэффициента трения f сила трения равна по величине fmg, где g—ускорение, и направлена всегда против движения. В отсутствие трения движение тела описывалось бы дифференциальным уравнением x+ω2x= 0, где ω—частота колебаний, равная ω=√k/т. В течение интервала времени 0< t < π√m/k, т. е. в первый полупериод колебания, тело двигалось бы налево. Если учесть трение, то при движении налево на тело действовала бы сила трения, равная fmg. Уравнение движения для этого временного интервала записывается следующим образом:
Из этого решения следует, что в момент времени t= π√m/k тело достигнет крайней левой точки х=—[А – (2mfg/k)], остановится, а затем начнет двигаться вправо. Даже без решения уравнения движения в следующий полупериод колебания ясно, что за половину периода сила трения каждый раз приводит к уменьшению амплитуды колебания на величину, равную 2mfg/k.
Чтобы размах колебания тела после n пересечений точки х=0 оставался больше В, необходимо, чтобы выполнялось неравенство
3
Необходимо найти величину х = х0, при которой это время минимально. Она находится из условия, чтобы первая производная dT/dx обращалась в нуль при х=х0:
Выполняя дифференцирование, получаем квадратное уравнение 1,8√x02 +362–3x0 = 0. Его положительный корень x0 = 27, что соответствует AK= 15 м.
Вычисляя вторую производную в точке х0 и подставляя в приближенную формулу х—х0 = ±3м, получаем Т = 60,1 сек. Точность этого приближения можно проверить непосредственным вычислением Т (x0 ±3) по точной формуле.
б) Время прохождения в воздухе t= 1 м/с (с—скорость света в воздухе). При наличии пластины полное время прохождения
26.3. Пусть b —толщина края линзы, d —ее толщина по оси, радиус h= 0,1м. Тогда времена прохождения равны: для «периферического» луча
Приравнивая их, получаем соотношение для определения d. Подставляя в него численные значения, получаем d ≈20 мм.
где с—скорость света в воздухе.
Исключая из них α и β, можно получить довольно громоздкое точное выражение для d через d′, D u n. Интересно простое приближенное выражение для случая, когда d«D. Тогда углы α и β (и, следовательно, α – β) малы, и в точном выражении d = d′n cos (α–β), следующем из выписанных соотношений, можно положить в первом приближении косинус равным единице. Тогда d = d′n.
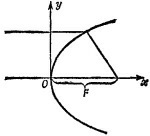
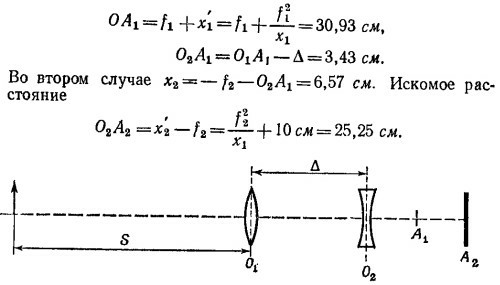
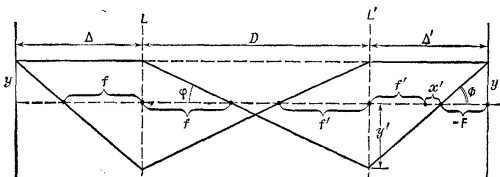
27.6. Пусть S = 10 м -расстояние от объекта до положительной линзы, Δ-расстояние между линзами, которые расположены в точках О1 и О2 соответственно (см. рисунок)
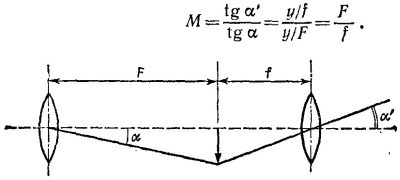
27.7. В обоих случаях нужно найти величину х′ — расстояние от главного фокуса до изображения; x′ = f`2/x, где f —фокусное расстояние, а х —расстояние до Луны или спутника. В случаях (а) и (б) соответственно получаем значения
27.8. Из определения главных плоскостей оптической системы следует их важное свойство: если точка находится в главной плоскости на расстоянии у от оптической оси, то ее изображение получается в другой главной плоскости на том же расстоянии от оптической оси. Этим свойством главных
К главе 28. Электромагнитное излучение
Геометрическая интерпретация: складываются N векторов длиной r, первый из которых направлен по оси абсцисс, а каждый последующий повернут относительно предыдущего на угол φ.
Для направлений, указанных на рис. 29.5 (см. «Лекции», вып. 3, стр. 52) получим
29.2. При указанной частоте расстояние между соседними излучателями равно четверти длины волны и, следовательно, полная разность фаз между ними в зависимости от угла есть Δφ=π/2(1 — sinθ). Поскольку интенсивность пропорциональна квадрату модуля амплитуды, можно воспользоваться результатом задачи 28.1 (б). Подставив в него N =4 и возводя в квадрат, находим
(λ—длина волны радиоизлучения). Сигналы равной амплитуды А от двух приемников смешиваются (векторно складываются), поэтому интенсивность I выходного сигнала есть
По условиям задачи минимально регистрируемое колебание интенсивности равно 10%, что соответствует (Δφ)2/4 = 0,1. Отсюда, полагая sin θ≈1, находим
В плоскости орбиты Еу′= 0 и интенсивность излучения пропорциональна cos2 [ωt — (r/с) — π/2]. На оси орбиты вектор электрического поля сохраняет свою длину и равномерно вращается, поэтому интенсивность от времени не зависит и вдвое превышает среднюю интенсивность в плоскости орбиты на том же расстоянии от источника.
Здесь N —число диполей в каждой линии; r —амплитуда каждого диполя; Δφ1 = π sin θ—сдвиг фаз между соседними диполями в каждой линии; Δφ2 = π/2(1— sin θ) —сдвиг фаз между соответствующими диполями в разных линиях. Модуль произведения комплексных чисел равен произведению модулей, поэтому интенсивность
Картина интенсивности, получающаяся в случае одного ряда диполей, «модулируется» в случае двойного ряда множителем
29.6. Ускорение каждого из электронов равно аω2 cos (ωt—φ0), и все электроны можно рассматривать как осцилляторы, излучающие в фазе. Если ρ—число электронов на единицу длины проволоки, их полное число равно Lρ и искомое поле находится согласно общей формуле
29.7. Вектор напряженности электрического поля излучения лежит в этом случае в вертикальной плоскости и длина его пропорциональна sin θ (см. рисунок в условии задачи, стр. 86). Следовательно, интенсивность излучения на заданном расстоянии От источника, пропорциональная среднему квадрату
К главе 30. Дифракция
Сложный спектральный состав белого света затрудняет разрешение двух источников — «изображения» их, соответствующие длинноволновой части спектра, сливаются раньше.
(Не путать ширину полосы с шириной линии, в спектре.)
(m — порядок спектра).
30.4. a) sin θi = —sin θd= sin θ и условие максимума имеет вид 2sin θ = mλ/d. Подставляя численные значения, получаем sin θ = 0,786, θ= 51,9°.
30.7. При каждом отражении амплитуда волны уменьшается в R раз. При каждом пересечении зазора фаза увеличивается на 2πD/λ. Амплитуда волны, испытавшей 2n отражений и 2n раз пересекшей зазор между поверхностями, есть
Суммарная амплитуда волны, падающей на правую поверхность, есть
а полная интенсивность равна А2. Следовательно, полная интенсивность прошедшего света есть
При R, близком к единице, как видно из полученного выражения, для тех длин волн, при которых фаза экспоненты равна четному числу π, интенсивность прошедшего света, равная (1— R2)/2, может быть очень велика. На этом свойстве и основано использование интерферометра как узкополосного оптического фильтра
31.2. Порядка 106 электронов в 1 см3.
31.4. а) Здесь удобно воспользоваться выражением для напряженности электрического поля
созданного зарядом q на расстоянии r от него в момент времени t, в направлении θ от оси движения заряда (см. «Лекции», вып. 3, стр. 47). Здесь а —ускорение заряда, равное, очевидно, —ω2x0 cos ωt. Следовательно,
Так как плотность потока энергии в электромагнитной волне равна ε0сЕ2, то мощность S, излучаемая через единицу поверхности на расстоянии r под углом θ, равна
Чтобы найти полную энергию Р, излучаемую в единицу времени электроном, усредним S за период движения (cos2ωt = 1/2) и умножим S на площадь, приходящуюся на элемент телесного угла dΩ:
б) Константа затухания, по определению, равна γR= P/W, где W—энергия, запасенная на одно колебание. Отсюда
К главе 32. Радиационное затухание, Рассеяние света
[сp. с выражением для γR найденным в задаче 31.4, гункт (б)].
32.3. Выражение для показателя преломления света имеет следующий вид [см. «Лекции», формула (31.19) вып. 3, стр. 91]:
Возводя обе части этой формулы в квадрат и поделив левую и правые части получающегося выражения на соответственно левую и правую части выражения для σ, получаем соотношение, из которого требуемый результат вытекает уже совсем просто.
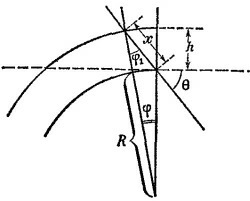
Зависимость х от угла θ, под которым Солнце стоит над горизонтом, можно определить геометрически (см. рисунок):
Подставляя это выражение и числовые данные задачи в формулу (1), получаем I (90°)/I0 (0) ≈е-0,32 = 73%; /(10°)/I0≈е-8 ≈3,5· 10-4.
где Ne —искомая плотность электронов; σ = 8π/3 (е2/mc2)2 = 6,25·10-25 см2 —томпсоновское сечение рассеяния. Этот рассеянный свет излучается сферой, радиус которой вдвое, а поверхность вчетверо больше поверхности Солнца. Поэтому отношение ее яркости к яркости солнечного диска (яркость в данном случае есть количество квантов, испускаемых единицей площади поверхности в единицу времени) есть r = R′/4. Поскольку для рассеянного излучения NeσR и, следовательно, показатель экспоненты в выражении (1) малы, то можно воспользоваться приближенной формулой е-х≈1—х. Тогда, приравнивая r численному значению из условия задачи, получаем r = 10-8 = NeσR/4; подставляя R = 7·1010 см, вычисляем
32.7. В гл. 31 «Лекций» получено выражение, связывающее количество энергии излучения, проходящей в 1 сек через 1 м2 поверхности, со средней напряженностью поля излучения в этой точке, S = ε0c<E>2 (P имеет размерность вт/м2, Е—в/м). Вспоминая формулу для джоулева тепла Q = V2/R, убеждаемся, что размерность величины ε0с—обратное сопротивление. Численное значение 1/ε0с = 377 ом.
где m — масса одной частицы. Подставляя m = 4/3πλ3ρ, ρ = 1 г/см3 (плотность льда) и λ = 5·10-5 см (видимый свет), получаем
32.9. а) Сечение рассеяния определяется как отношение полной энергии, излучаемой рассеивающей системой в секунду, к энергии радарного луча, падающей на 1 м2 в 1 сек. Все электроны проволоки из-за малой ее длины можно считать колеблющимися в фазе, тогда мож/ю воспользоваться результатами задачи 29.6 (стр. 275),где для такого случая было получено выражение для поля излучения на больших расстояниях r от проволоки под углом θ к ее оси. Перепишем полученное там выражение в обозначениях данной задачи:
Интенсивность излучения S = εoc<E2>. Интегрируя ее по сфере радиусом r (см. «Лекции», § 2 гл. 32, вып. 3, стр. 103) и подставляя среднее по времени значение квадрата косинуса, равное 1/2 получаем среднюю энергию, излучаемую по всем направлениям:
Относя ее к среднему потоку в радарном луче Рр=ε0сЕ02/2, получаем выражение для сечения
К главе 33. Поляризация
33.2. Выберем ось х по оси первого поляроида и примем амплитуду неполяризованного светового пучка за единицу. Тогда после прохождения первого поляроида составляющие амплитуды по осям будут
После прохождения второго поляроида
33.3. При падении света под углом Брюстера прошедший и отраженный лучи взаимно перпендикулярны, т. е. sin r = cos i, поэтому
что и требовалось показать.
где d —расстояние, пройденное светом. Полагая φ = π/2 и произведя вычисления, находим
33.6. Используя формулы Френеля для интенсивности отраженных волн с разной поляризацией, получаем для неполяризованного света
(i =80° по условиям задачи). Зная коэффициент преломления воды n=1,33, находим r = 48°. Для этих численных значений I/I0≈35%.
б) Угол Брюстера φ = arctg n = 67,5°.
Таким образом, вектор амплитуды вышедшей волны можно записать в виде
эллиптически поляризованный свет (см. «Лекции», фиг. 33.2, вып. 3, стр. 118).
34.2. Искомое ускорение находится двукратным дифференцированием х по t
дифференцированием выражений, полученных в предыдущей задаче:
По условию задачи требуется выразить результат через наблюдаемые величины R, v = cR/A и х (см. «Лекции», § 2 гл. 34, вып. 3, стр. 136). Заменяя в полученном выражении R cos θ на х, а А на cR/v, получаем
34.3. Интенсивность излучения пропорциональна квадрату поля, а оно в свою очередь пропорционально «запаздывающему» ускорению частицы. Подставляя в формулу для ускорения, полученную в предыдущей задаче, x = R и значения скорости +v и —v, получаем
34.4. Выберем ось х неподвижной системы координат по направлению движения Земли, а ось у —по направлению луча (предполагая, что оно перпендикулярно оси х). Оси движущейся системы координат, связанной с Землей, обозначим х′ и у′ соответственно, направив их параллельно осям х и у. Проекции волнового вектора света звезды в неподвижной системе по условию равны kx = 0, ky=k = ω/с. Скорость движущейся системы относительно неподвижной равна v. Согласно преобразованию Лоренца,
Следовательно, в системе координат, связанной с Землей, волновой вектор образует с осью у угол, тангенс которого равен
отсюда получаем для угла аберрации sin θ = v/с.
Масса Земли mЗ сокращается. Подставляя значения солнечной массы и гравитационной постоянной G = 6,67·10–8см3/г·сек, получаем
34.9. а) Сила гравитационного притяжения убывает обратно пропорционально квадрату расстояния от Солнца. Сила светового давления пропорциональна импульсу, переданному частице за единицу времени поглощенным излучением, а импульс в свою очередь — энергии излучения на единицу площади, т. е. интенсивности (~L~-2). Таким образом, силы светового давления и притяжения одинаково зависят от L и их отношение, следовательно, постоянно.
где L — радиус земной орбиты, а v —скорость движения Земли по ней, вычисленные в предыдущей задаче, получаем после сокращения
если выражать ρ в г/см3.
и для «времени жизни» возбужденного состояния свободного атома (времени, в течение которого энергия убывает в е раз за счет излучения)
(здесь Q—классическая величина радиационного затухания). Если записать энергию возбужденного состояния в соответствии с квантовыми представлениями как E=hω, то с помощью вышеприведенных соотношений получаем квантовое соотношение неопределенности для энергии и времени
Заметим далее, что «неопределенность положения» фонона Δx есть по смыслу длина отвечающего ему волнового пакета, равная сΔТ. Неопределенность импулься Δр связана с шириной спектральной линии Δλ и равна Δр = (h/λ2) Δλ (так как р = h/λ). Итак,
38.2. а) В задачу об определении радиуса электронной орбиты входят следующие константы: постоянная Планка h, масса электрона m и константа, характеризующая силу притяжения между электроном и протоном; в качестве такой величины возьмем е2 (е2 = qe2/4πε0). Размерности этих констант соответственно: энергия X время, масса, энергия X длина. Вспоминая размерность энергии, нетрудно убедиться, что единственная комбинация из этих констант, имеющая размерность длины, есть h2/me2 = а0. Это и есть боровский радиус.
Эта энергия по порядку величины равна искомой энергии ионизации.
и равны 4860, 6560 и 1880 Å.
39.2. Так как процесс сжатия воздуха можно считать адиабатическим, то, согласно результату предыдущей задачи, можно написать соотношение
где индексами 1 и 2 помечены, температура и давление воздуха до и после сжатия. Из этого соотношения следует
39.3. а) В первом процессе газ, расширяясь, не совершает никакой работы. Следовательно, его энергия, а потому и температура остаются постоянными, т. е. T=T0. Так как V = 2V0, из закона идеального газа следует, что Р=Р0/2.
где Р0, V0, T0 —давление, объем и температура газа гелия в исходном состоянии.
Отсюда и следует искомое уравнение.
которое следует из закона идеального газа PV = NkT. Поэтому мы получаем уравнение
Интегрируя, находим Р = Р0е–μgh/RT, где Р0 — давление у поверхности Земли, т. е. при h = 0.
Дифференцируя левую и правую части этого соотношения по высоте и учитывая уравнение dP/dh=–ρ (h)g (см. задачу 35.4), находим
Согласно закону идеального газа, ρ0Т0/Р0 =μ/R, где μ —молекулярный вес, R —газовая постоянная. Таким образом, окончательно находим
Так как для воздуха μ = 29, γ= 1,4, то dT/dh= — 9,75 град/км.
Подставляя последнее соотношение в левую часть приведенного выше неравенства и учитывая тот факт, что dP/dh = — ρg, находим
39.6. Работа, затрачиваемая при изотермическом процессе на сжатие от объема V1 до объема V2, равна
39.8. Работу, необходимую для адиабатического сжатия, легко найти, если учесть, что Р0V0γ=PVγ:
39.9. Для конечного состояния системы можно написать уравнения
где N — полное число молекул газа. Число N нетрудно найти, если написать аналогичное уравнение для исходного состояния системы N = Р0 (V1+V2)/kТ0, где Р0 и Т0 —начальное давление и температура системы. Подставляя во второе из написанных уравнений выражение для N1, полученное из первого уравнения N1 = РV1/kT1, легко находим
39.10. Обозначим через Р1, N1 и Р2, N2 давления и числа молекул в большом и малом резервуаре после нагрева до температуры T = 162°С = 435°К. По условию задачи Р1 — Р2 =Р0= 88 см рт. ст. Обозначим через N полное число молекул газа. Очевидно, N = N1+N2 = PV1/kT0, где Р = 760 мм рт.ст. — атмосферное давление, Т0 = 17° С = 290° К — начальная температура. Для конечного состояния можно написать два уравнения:
39.11. Число образовавшихся молекул NO2 равно N = PV/kT. Так как молекулярный вес двуокиси азота равен 46, то х —число граммов диссоциировавшей жидкости определится как х = 46N/NAB = 46PV/PT = 0,6 г. Следовательно, диссоциировало 66% четырехокиси азота.
б) В конечном состоянии газа P1V2 = RT2. Учитывая, что в начальном состоянии P1V1 = RT1, находим V2/V1 = T2/T1 = 5,8. Работа, совершенная газом, равна
К главе 40. Принципы статистической механики
Так как разность сил, действующих на рассматриваемое крылышко, равна изменению импульса крылышка за единицу времени, то F = Δpv =П/v. Разумеется, при строгом решении задачи следовало бы учесть, что изотропно отскакивающие молекулы уносят различные значения импульса, так как они вылетают под разными углами к поверхности. Однако при этом мы получили бы численный коэффициент, который был бы порядка единицы. Столь же нестрого определим среднюю скорость молекул как скорость, удовлетворяющую соотношению
40.2. Пусть поверхность сосуда совпадает с плоскостью координат уz, а ось х перпендикулярна к ней. Тогда dnVx—число частиц в единице объема, х—проекция скорости которых заключена в интервале vx, vx+dvx, равно
где n0 —число частиц газа в единице объема. Ясно, что из этих частиц только те достигнут за единицу времени поверхности сосуда, т. е. плоскости yz, которые расположены от нее не далее расстояния, численно равного vx, т. е. их число равно
Следовательно, v — полное число частиц, которые за единицу времени достигнут поверхности сосуда, равно
где v = √8kT/πm —средняя тепловая скорость молекулы газа. Скорость v находится с помощью распределения Максвелла:
можно интерпретировать как число молекул, достигших единичной площадки поверхности сосуда в единицу времени, энергия которых заключена в пределах ε, ε+dε.
40.3. Теплоемкость при постоянном объеме определяется как производная от внутренней энергии газа по температуре CV=dU/dT.
40.4. Законы сохранения массы, импульса и энергии требуют, чтобы потоки этих величин слева и справа от сетки равнялись друг другу.
Найдем далее выражение для потока импульса. В газе, который как целое покоится, плотность потока импульса, очевидно, равна
где n —число молекул в единице объема; m —масса молекулы (ρ= nm), а усреднение производится с помощью распределения частиц по скоростям. Действительно, импульс одной молекулы в направлении к сетке (выберем его за направление оси х) равен mvx, а поток импульса mvx2. Если умножить mvx2 на n, то получаемая при этом величина будет равна плотности потока импульса в направлении х, обусловленная всеми частицами, компонента скорости которых равна vx. Так как частицы в газе распределены по скоростям, величину nmvx2 следует усреднить по всем скоростям. При этом получаем естественный результат: плотность потока импульса равна Р—давлению в газе [см. «Лекции», § 2 гл .39, формула (39.5), вып. 4, стр. 10]. Если же газ как целое движется со скоростью v в направлении оси х, то простое обобщение формулы для плотности потока импульса приводит к выражению
Здесь мы использовали тот факт, что <vx> = 0.
Рассуждая аналогично, находим далее выражение для плотности потока энергии
Внимательно вглядевшись в наши выкладки, мы видим, что слагаемое 3/2 Р/ρ есть не что иное, как U — энергия единицы массы газа. Как отмечалось в «Лекциях», множитель 3/2 появляется лишь в рассматривавшейся выше модели одноатомного газа. В общем случае его нужно заменить на 1/(γ—1), где γ —газовая постоянная. Если это сделать, то закон сохранения энергии в данной задаче запишется в виде
Используя далее закон сохранения массы и импульса и вводя обозначение γР/ρ = γRТ/μ = с2, где с —скорость звука, из закона сохранения анергии получаем квадратное уравнение для v′
40.5. Основной характеристикой, определяющей достоинства двигателя, является его коэффициент полезного действия. Он равен отношению полезной мощности, развиваемой двигателем к полным энергетическим затратам. Если реактивный двигатель развивает силу тяги F и летит со скоростью v, то, очевидно, полезная мощность, развиваемая им, равна Fv. С другой стороны, полная затраченная энергия равна q = GH, где G — расход горючего в единицу времени, а Н — теплотворная способность горючего. Отсюда
Заметим, что в данной задаче, строго говоря, в законах сохранения следовало бы учитывать массу горючего, сжигаемого в двигателе и выбрасываемого с воздухом. Однако, поскольку расход горючего по условию задачи мал по сравнению с расходом воздуха, мы этим эффектом пренебрежем. При достаточно малых скоростях и величинах q приведенное выше выражение для к. п. д. упрощается, если разложить подкоренное выражение по малой величине q. При этом оказывается, что к. п. д. двигателя не зависит от q и определяется только скоростью полета:
Так как, согласно условию задачи, Аj= 100 кг/сек, q = 9,3·107 вm, γ = 9/7 и, кроме того, при нормальных условиях с=340 м/сек, то, принимая скорость v равной обычной крейсерской скорости полета реактивных самолетов, т. е. примерно 800 км/час, находим
К главе 41. Броуновское движение
К главе 42. Применения кинетической теории
43.2. Вероятность того, что молекула пройдет путь L без столкновения, равна e–L/l. Из N молекул путь L пройдет без столкновения лишь Ne–L/l молекул. Если, как это требуется в условии задачи, Ne–L/l < 1/2, то L > I ln 2N≈56l.
(рассматриваются молекулы, находящиеся на расстоянии –l влево и +l вправо от выделенной плоскости). Из того факта, что Q =–KdT/dx, следует
где С = nk/(γ—1)—теплоемкость единицы объема газа. Если пренебречь численным коэффициентом 1/3. появившимся из-за приближенности расчета, то получим искомый результат.
Нетрудно видеть, что из этого выражения следует искомый результат.
43.6. Подвижность иона массы m в газе определяется его средней скоростью v и длиной свободного пробега l:
Если nA0 и nB0—число молекул в единице объема исходных газов A и В, то можно написать соотношения
где σA и σB—полные сечения рассеяния иона на молекулах сорта A и В. Плотности газов выражаются через массы составляющих его молекул формулами ρA=mAnA0 и ρB = mBnB0. В смеси газов, в единице объема которой содержится nA молекул сорта A u nB молекул сорта В, величина, обратная длине свободного пробега иона, равна 1/l= σAnA+ σBnB. В этом нетрудно убедиться, если рассуждать точно так же, как при выводе выражения для l через полное сечение σ и число молекул в единице объема n в случае однокомпонентного газа. Поэтому подвижность иона в смеси газов равна
Плотность смеси газов равна ρ=ρА+ρB = mАnА + mBnB= =mАnА0 +mBnB0. Отсюда, положив nА=nА0 и nB= nB0, находим
К главе 44. Законы термодинамики
44.3. Для цикла Карно
44.4. а) Из уравнения адиабаты в V—Т переменных (см. решение к задаче 39.1) следует, что
44.5. Так как процесс расширения является изотермическим, (см. решение задачи 44.2), то
К главе 45. Примеры из термодинамики
Так как RΘ = Lα/2, где α—угол, под которым виден диаметр Солнца с Земли, а интенсивность энергии, излучаемой медной сферой с температурой T1, равна 4πr2σТ14, то из условия теплового баланса
45.2. Максимальную температуру этой области Земли следует определить из условия 1395 вт/м2 = 5,67· 10-8 вт/м2·град4· T4, Т = 122° С.
Следовательно, отношение энергии, излучаемой оболочкой в единицу времени во внешнее пространство (4πR2σT14), к интенсивности излучения энергии в отсутствие ее (4πr2σT4), равно R2/(r2 + R2). В столько же раз уменьшится скорость охлаждения тела.
где VG—объем газа, L—скрытая теплота испарения массы воды VG/ρG. Давление пара с высотой падает по закону dPnap/dz=—ρg (ρ—плотность воздуха). Следовательно (ρ= 1,3 кг/м3):
45.6. Теплоемкость С тела равна производной от сообщенного телу тепла Q по температуре: C = dQ/dT. При постоянном давлении dQ = dH, т. е. сообщенное тепло равно изменению энтальпии. Поэтому Cp = dH/dT. При постоянном объеме dQ = dU, где U—внутренняя энергия тела. Следовательно, CV=dU/dT. Энтальпия и внутренняя энергия связаны соотношением H=U+PV. Дифференцируя левую и правую части этого соотношения по температуре, находим Cp = CV+(d/dT) PV. Так как, согласно закону идеального газа, PV = RT, то Сp—CV=R.
где VL—объем 1 моля жидкости, VG—объем 1 моля вещества в твердом состоянии (см. «Лекции», вып. 4, стр. 135). Так как L > 0, то при VG > VL (если вещество при замерзании расширяется) dP/dT < 0, или dT/dP < 0, т. е. температура замерзания должна понижаться с повышением давления.
где Т0—постоянная интегрирования. Определим Т0 из условия, что при нормальном давлении Р0 = 1 атм температура таяния льда равна 0° С, т. е. 273° K:
Подсчитаем далее примерное давление Р, которое оказывает лезвие конька на лед. Длина конька примерно равна 40 см, а ширина лезвия 2 мм. При этом площадь лезвия конька оказывается равной 8 см2. Принимая средний вес человека равным 80 кГ и считая, что этот вес распределен по площади одного конька, находим ΔР = Р—Р0 =9·104 кГ/м2 = 8,8 ньютон/м2. Так как ΔV = VG— VL = 8·10-5 м3 и L = 334 дж/кГ, то находим
К главе 47. Звук. Волновое уравнение
47.2. Так как частота звука, издаваемого свистком, пропорциональна скорости звука (см. гл. 49 «Лекций», вып. 4), а последняя ~√Т, то искомая температура в шкале градусов Кельвина в 4 раза больше температуры жидкого воздуха, т. е. равна 372°K=99°C.
47.4. Изменение давления ΔР в звуковой волне связано с изменением плотности Δρ соотношением ΔР = сs2Δρ, где сs —скорость звука.
47.5. Частоты колебания резины пропорциональны корню квадратному из отношения натяжения Т к линейной плотности σ (см., например, решение к задаче 47.6) и обратно пропорциональны ее длине, т. е. ω ~ (1/L) √T/σ. Так как T~L, σ~1/L, то ясно, что частоты колебания такой резины не зависят от ее длины. Поэтому высота звука такой «струны» будет все время одинаковой. Иначе обстоит дело для скрипичной струны, поскольку для струны σ = const и L = const. Поэтому с увеличением натяжения струны звук получается более высокой частоты.
Уравнение движения для выделенного участка струны запишется в виде
Сокращая на dx обе части получившегося уравнения и вводя обозначение v2 = Т/σ, находим искомое волновое уравнение
47.7. Решение тривиально.
48.4. Для искомой длины волны dvфаз/dλ = 0. Из этого уравнения следует
48.5. Частота звука, регистрируемая от какого-либо источника, согласно эффекту Допплера, зависит как от скорости источника звука, так и наблюдателя. Если наблюдатель покоится, а источник звука движется со скоростью v к наблюдателю или от него (последнему случаю отвечает знак минус в приведенной ниже формуле), то частота регистрируемого звука равна
где ω0 — частота звука, испускаемого покоящимся источником. Так как ω0 = 340 гц, cs = 340 м/сек, v =5 м/сек, то Δω = 5 гц.
С учетом того, что k1/m1 = k2/m2 = ω02 эту систему дифференциальных уравнений можно привести к виду
49.2. Будем искать решение полученной в предыдущей задаче системы уравнений в виде х = Ае`iωt и y = Beiωt. Выполняя необходимые дифференцирования и сокращая уравнения на eiωt,находим
Введя обозначение λ= ω2—ω02, запишем эту систему однородных уравнений в виде
Отличное от нуля решение этой системы существует только в том случае, если детерминант, составленный из коэффициентов этой системы уравнений, обращается в нуль, т. е. если
Раскрыв определитель, получим квадратное уравнение, имеющее два вещественных решения λ1= 0 и λ2 =k(m1-1+m2-1).Следовательно,
Подставляя ω12 в систему уравнений, находим, что А = В. Для частоты ω2 получим
Таким образом, произвольное решение уравнений движения имеет вид
Отсюда видно, что линейные комбинации координат х и у
являются нормальными координатами системы, так как они удовлетворяют уравнениям
49.3. Решение тривиально.
где ω0=vπ/а. Наименьшая частота, очевидно, равна ω0/3. Десять искомых частот, измеренных в единицах ω0/3, равны 1; 1,665; 2,05; 2,22; 2,78; 3,33; 3,50; 3,76; 3,93; 4,04; 4,33.
К главе 50. Гармоника
Разделив на численный множитель, стоящий перед суммой ряда, получим требуемый результат.
50.2. Заданная функция имеет вид
50.3. а) Воспользуемся «теоремой об энергии» (см. «Лекции», вып. 4, стр. 213):
Нетрудно видеть, что отсюда следует искомый ответ,
50.4. Задача легко решается, если вспомнить, что при q < 1
Если интегрировать почленно и в n-м члене (n—любое) делать замену переменной интегрирования и=nх, то мы придем к результату
Так как, согласно задаче 50.3, сумма ряда, стоящего перед интегралом, равна π4/90, а сам интеграл равен 6, то отсюда следует искомый результат.
Искажение волны, следовательно, сводится к изменению амплитуды основной гармоники и появлению третьей гармоники. Эффект выпрямления отсутствует,
Члены, содержащие синусы в кубе, можно разложить по гармоникам, используя решение к пункту (а) этой задачи. Остальные члены разложим по синусам и косинусам. Например,
Таким образом, помимо изменения амплитуд колебания основных гармоник, кубическая нелинейность приводит к появлению новых колебаний с частотами Зω1, 2ω1 ± ω2, ω1± 2ω2, 3ω2. Эффект выпрямления отсутствует. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

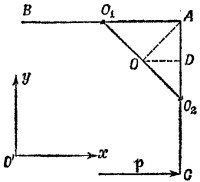 20.6. Центр масс системы двух стержней находится в точке О, делящей отрезок О1О2 пополам (О1, О2 —центры стержней). После удара в точку С стержни придут в движение, которое можно разложить на два: поступательное движение системы как целого со скоростью v по линии удара и вращательное вокруг центра масс О с некоторой угловой скоростью ω. Пусть m и l —масса и длина каждого из стержней, а р — переданный в результате удара импульс. Из закона сохранения импульса 2mv = p следует, что скорость поступательного движения системы равна v = p/2m, а из закона сохранения момента количества движения Iω=pDC, что ω = (3pl/4I)(DC=3/4l), где I —момент инерции стержней относительно центра масс системы.
20.6. Центр масс системы двух стержней находится в точке О, делящей отрезок О1О2 пополам (О1, О2 —центры стержней). После удара в точку С стержни придут в движение, которое можно разложить на два: поступательное движение системы как целого со скоростью v по линии удара и вращательное вокруг центра масс О с некоторой угловой скоростью ω. Пусть m и l —масса и длина каждого из стержней, а р — переданный в результате удара импульс. Из закона сохранения импульса 2mv = p следует, что скорость поступательного движения системы равна v = p/2m, а из закона сохранения момента количества движения Iω=pDC, что ω = (3pl/4I)(DC=3/4l), где I —момент инерции стержней относительно центра масс системы.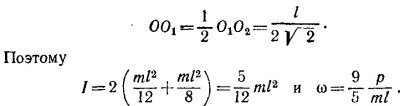
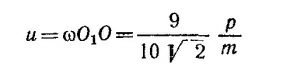
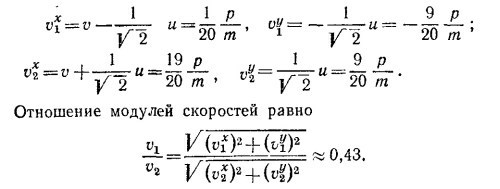
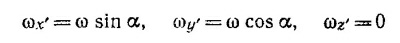
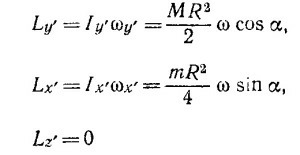
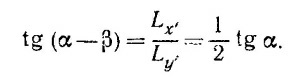
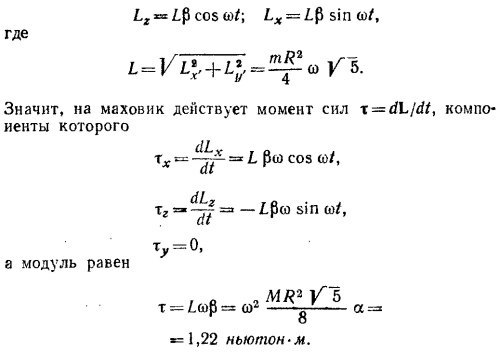
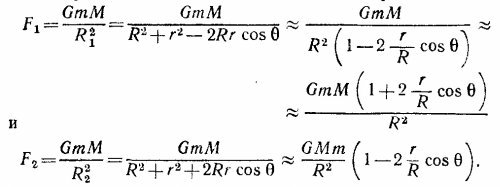
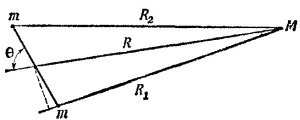 При получении приближенных формул мы пренебрегли r2 по сравнению с R2 и учли, что (r/R) cos θ«1, воспользовавшись соотношением 1/(1±х) ≈ 1±х при х«1. Вращающий момент τ равен разности моментов сил F1 и F2 относительно точки О, так что |τ| = F1rsin θ—F2rsin θ (плечи обеих сил приближенно равны r sin θ).
При получении приближенных формул мы пренебрегли r2 по сравнению с R2 и учли, что (r/R) cos θ«1, воспользовавшись соотношением 1/(1±х) ≈ 1±х при х«1. Вращающий момент τ равен разности моментов сил F1 и F2 относительно точки О, так что |τ| = F1rsin θ—F2rsin θ (плечи обеих сил приближенно равны r sin θ).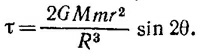
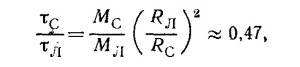

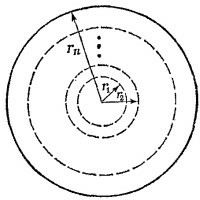 Землю представим себе состоящей из нескольких шаровых слоев, плотность внутри каждого из которых постоянна и равна полусумме плотностей на радиусах слоя. Там, где имеется разрыв плотности, большее значение ее будем приписывать внутренней части слоя, а меньшее — внешней.
Землю представим себе состоящей из нескольких шаровых слоев, плотность внутри каждого из которых постоянна и равна полусумме плотностей на радиусах слоя. Там, где имеется разрыв плотности, большее значение ее будем приписывать внутренней части слоя, а меньшее — внешней.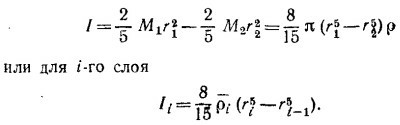
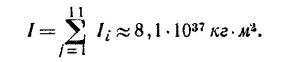
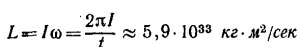
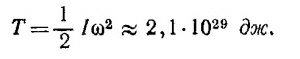
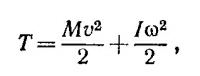
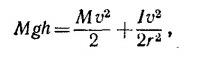
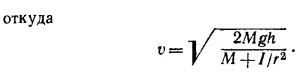

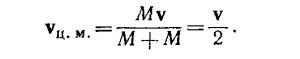
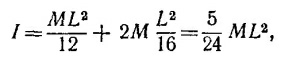
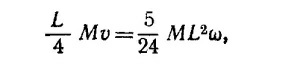

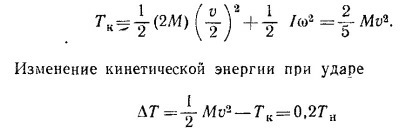
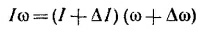
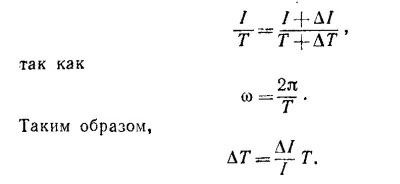
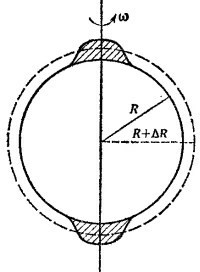 Изменение момента инерции Земли ΔI произошло за счет того, что вода, сосредоточенная ранее (в виде льда) вблизи оси вращения (и поэтому дававшая очень малый вклад в момент инерции Земли), расстаяв, распределилась по шаровому слою радиусом R и толщиной ΔR. Момент инерции такого слоя (см. задачу 20.10):
Изменение момента инерции Земли ΔI произошло за счет того, что вода, сосредоточенная ранее (в виде льда) вблизи оси вращения (и поэтому дававшая очень малый вклад в момент инерции Земли), расстаяв, распределилась по шаровому слою радиусом R и толщиной ΔR. Момент инерции такого слоя (см. задачу 20.10):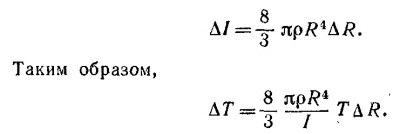
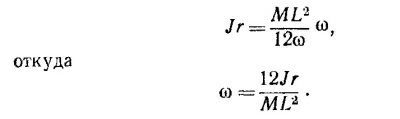
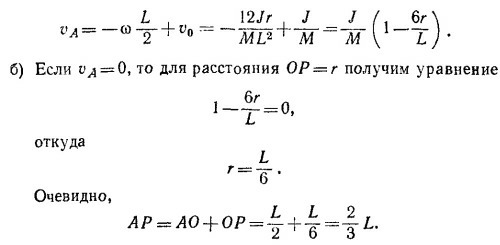
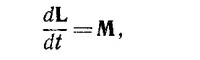
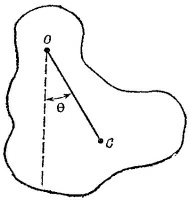 где L — момент количества движения, а М — момент внешних сил.
где L — момент количества движения, а М — момент внешних сил.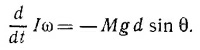
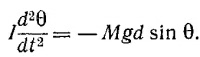
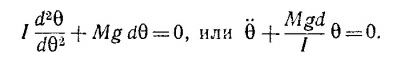
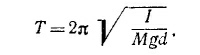
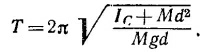

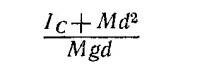
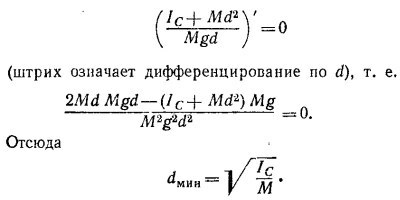
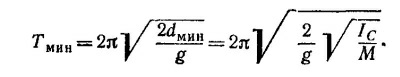
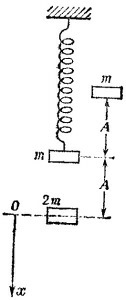 21.3. Из того, что пружина под действием силы веса груза массой m удлиняется на А, находим ее коэффициент жесткости k = mg/A.
21.3. Из того, что пружина под действием силы веса груза массой m удлиняется на А, находим ее коэффициент жесткости k = mg/A.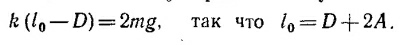
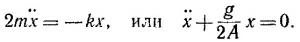
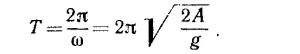
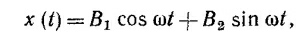
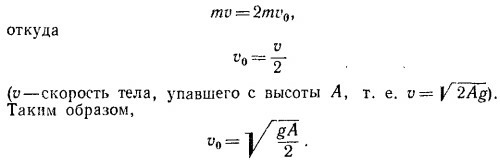
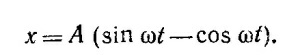
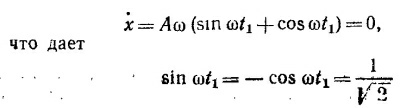
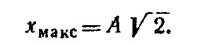
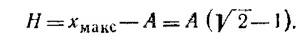
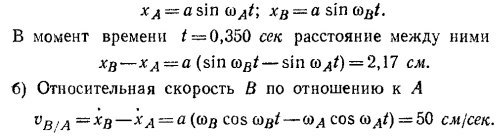
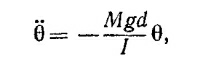
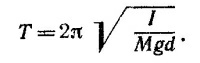
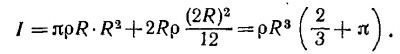
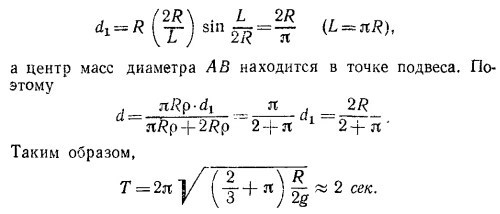
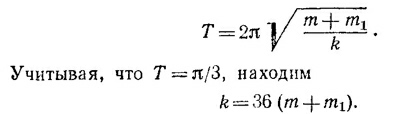
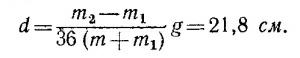
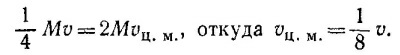
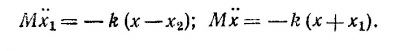
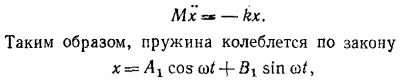
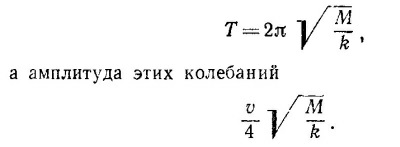
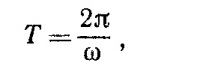
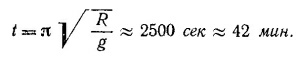
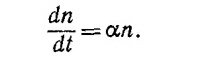
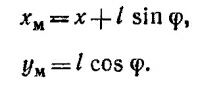
 где I —длина маятника.
где I —длина маятника.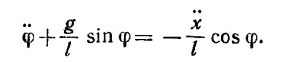
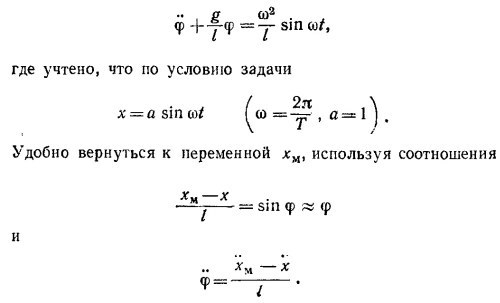
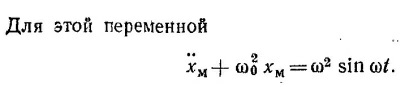
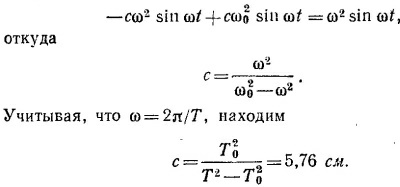
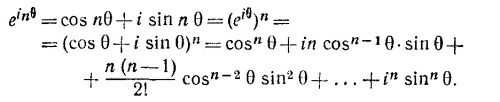
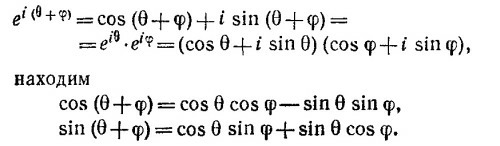
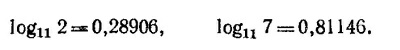

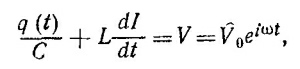
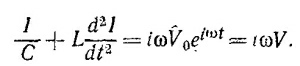
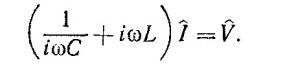
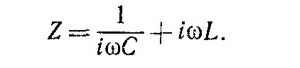
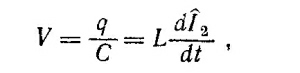
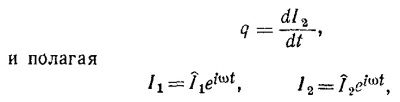
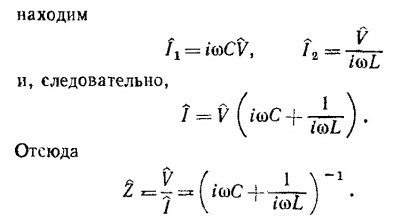
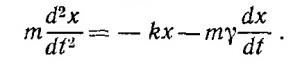
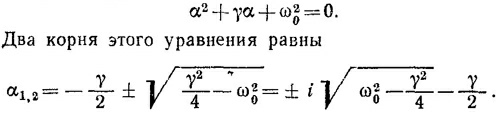
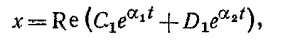
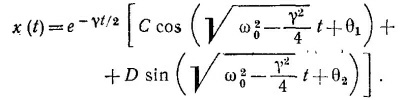
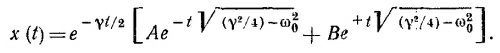

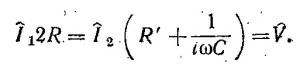

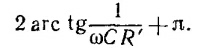
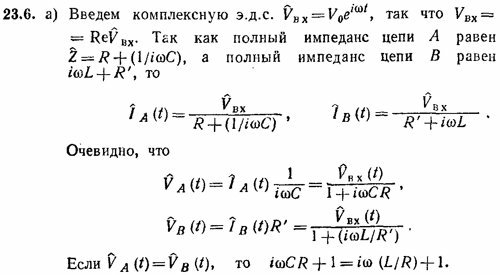
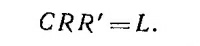
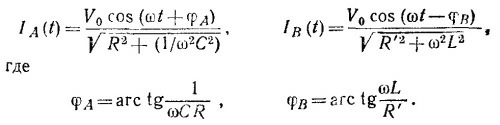
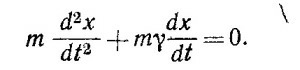

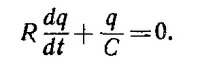
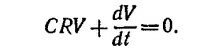
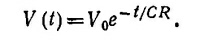
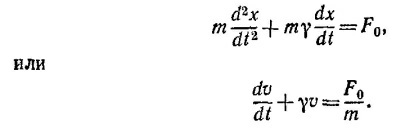
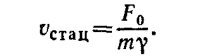
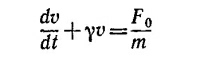
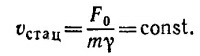
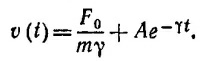
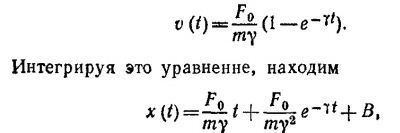
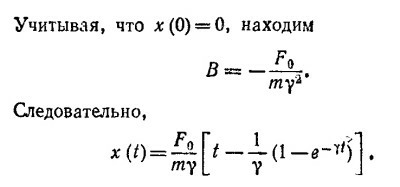
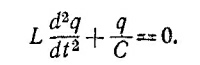
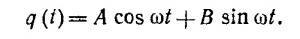
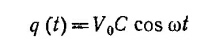
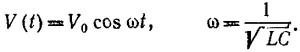
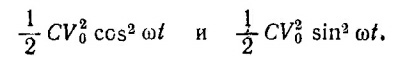
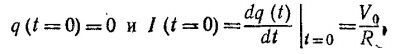
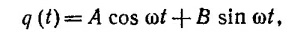
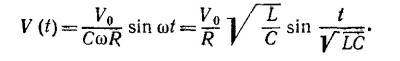
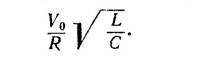
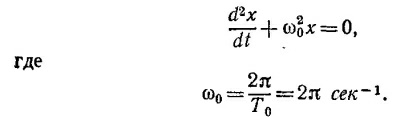
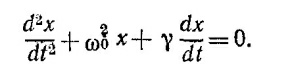
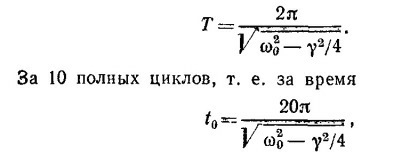
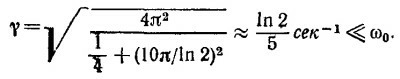

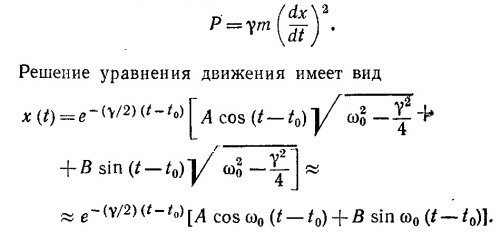
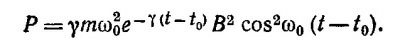
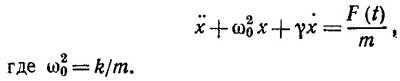

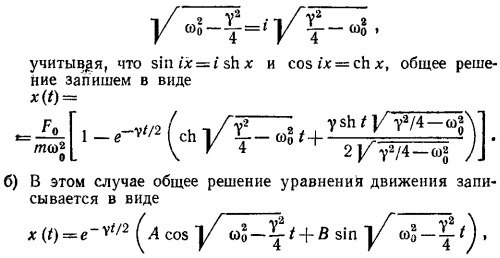
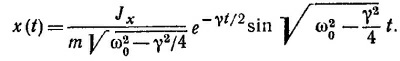

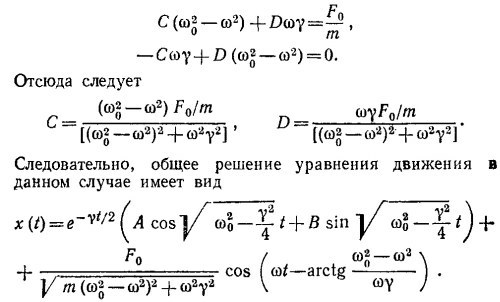
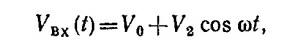
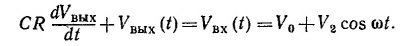
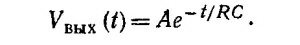
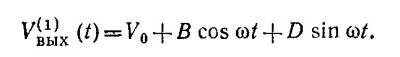
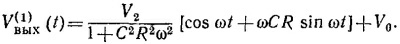
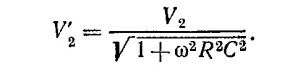
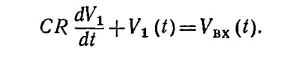
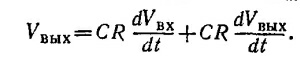
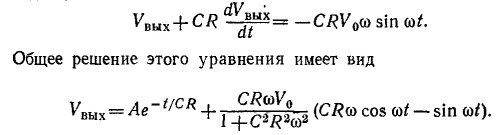
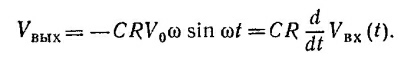
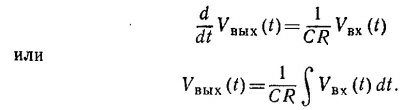
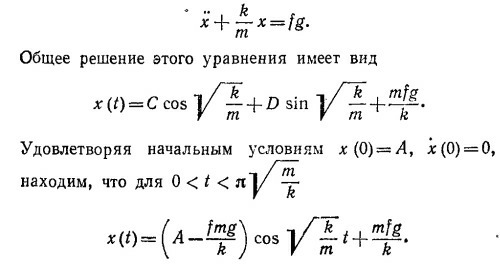
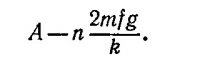
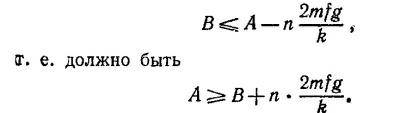
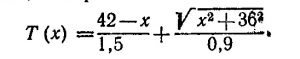
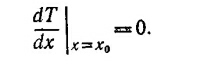
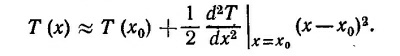
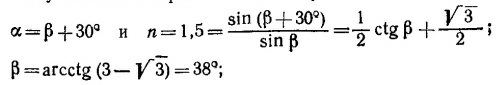
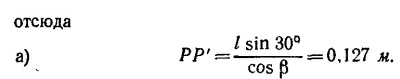
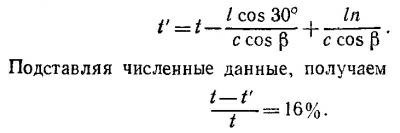
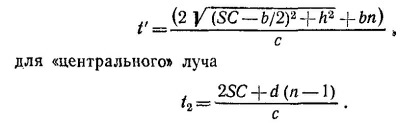
 27.1. Время хода для осевого луча должно быть равно времени хода для произвольного луча, проходящего через точку с координатами х и у, лежащую на преломляющей поверхности. Разность этих времен равна
27.1. Время хода для осевого луча должно быть равно времени хода для произвольного луча, проходящего через точку с координатами х и у, лежащую на преломляющей поверхности. Разность этих времен равна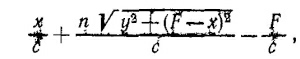
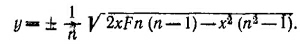
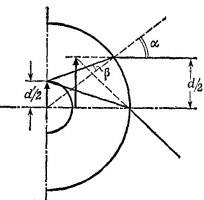 27.2. На рисунке изображен поперечный разрез капиллярной Трубки. Нужно построить изображение радиуса капиллярного отверстия, создаваемое стенкой трубки, которая действует как толстая цилиндрическая линза. Способ построения ясен из чертежа; из закона преломления и рассмотрения треугольников на рисунке вытекают следующие соотношения:
27.2. На рисунке изображен поперечный разрез капиллярной Трубки. Нужно построить изображение радиуса капиллярного отверстия, создаваемое стенкой трубки, которая действует как толстая цилиндрическая линза. Способ построения ясен из чертежа; из закона преломления и рассмотрения треугольников на рисунке вытекают следующие соотношения: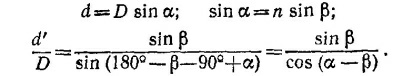
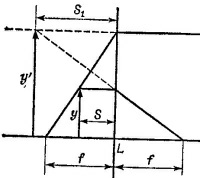 27.5. Поскольку глаз располагается вплотную за линзой, он может рассматривать лишь мнимое изображение, располагающееся по ту же сторону линзы, что и предмет (см. рисунок). Для получения мнимого изображения предмет должен быть расположен между фокусом и линзой, и в формуле линзы нужно брать отрицательное расстояние S1:
27.5. Поскольку глаз располагается вплотную за линзой, он может рассматривать лишь мнимое изображение, располагающееся по ту же сторону линзы, что и предмет (см. рисунок). Для получения мнимого изображения предмет должен быть расположен между фокусом и линзой, и в формуле линзы нужно брать отрицательное расстояние S1: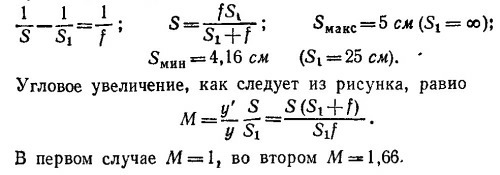
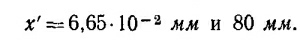
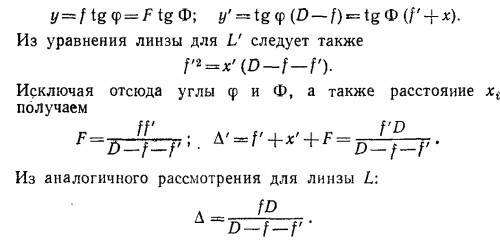
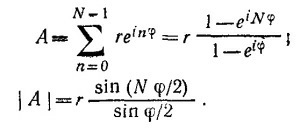
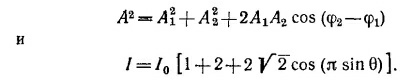
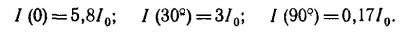
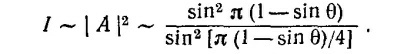
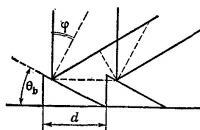
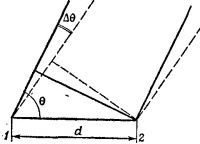 29.3. На рисунке схематически изображен радиотелескоп с расстоянием между чашами-приемниками 1 и 2, равным d. Телескоп регистрирует сигналы от удаленного источника. Малое изменение углового положения источника приводит к фазовому сдвигу Δφ между сигналами, поступающими в приемники. Этот сдвиг по общей формуле связан с углом Δθ следующим образом:
29.3. На рисунке схематически изображен радиотелескоп с расстоянием между чашами-приемниками 1 и 2, равным d. Телескоп регистрирует сигналы от удаленного источника. Малое изменение углового положения источника приводит к фазовому сдвигу Δφ между сигналами, поступающими в приемники. Этот сдвиг по общей формуле связан с углом Δθ следующим образом: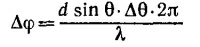
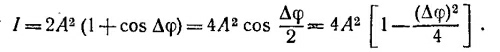
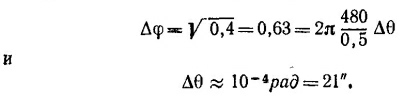
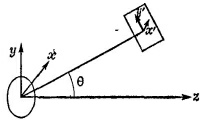 29.4. Круговое движение есть наложение двух колебаний во взаимно перпендикулярных направлениях с разницей фаз π/2 (см. «Лекции», § 1 гл. 33, вып. 3, стр. 116). Компоненты электрического поля в плоскости, перпендикулярной лучу (см. рисунок), согласно формуле (29.3) «Лекций» (вып. 3, стр. 49), равны
29.4. Круговое движение есть наложение двух колебаний во взаимно перпендикулярных направлениях с разницей фаз π/2 (см. «Лекции», § 1 гл. 33, вып. 3, стр. 116). Компоненты электрического поля в плоскости, перпендикулярной лучу (см. рисунок), согласно формуле (29.3) «Лекций» (вып. 3, стр. 49), равны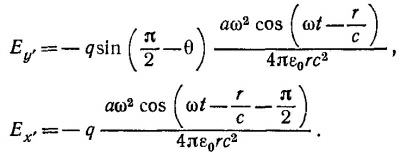
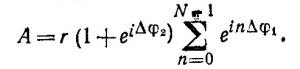
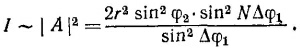
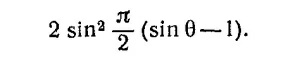
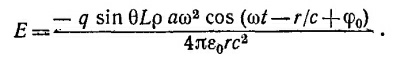
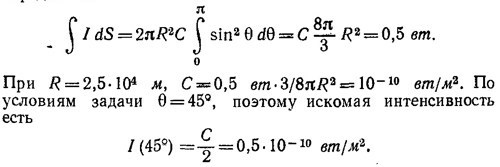
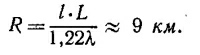
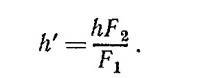
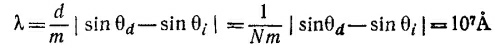
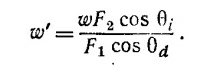

 где m —порядок спектра. При значительной величине угла φ равенство (2) может выполняться лишь для достаточно высоких порядков.
где m —порядок спектра. При значительной величине угла φ равенство (2) может выполняться лишь для достаточно высоких порядков.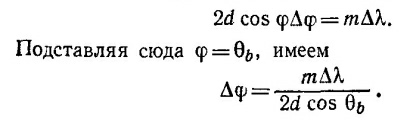
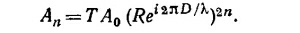
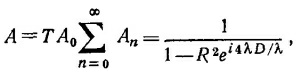
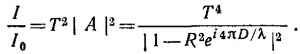
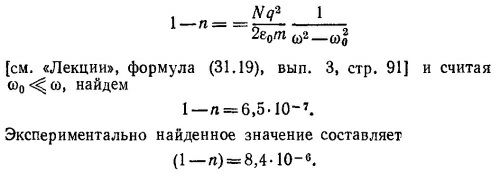
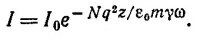
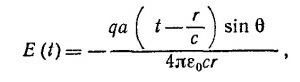
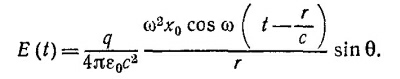
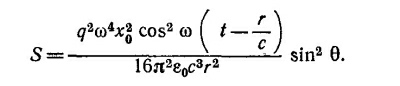
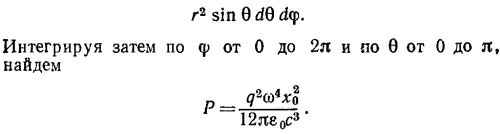
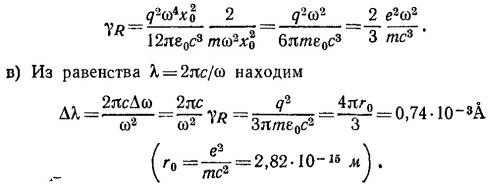
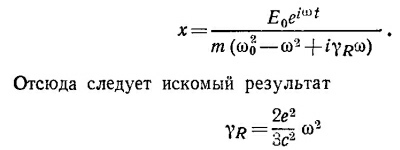
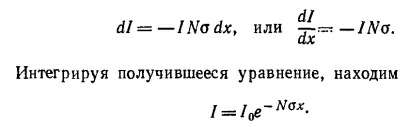
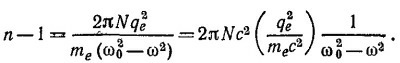
 32.4. Воспользуемся результатами задач 32.2 и 32.3. Для воздуха n—1=0,000292; при атмосферном давлении число молекул в единице объема N = 6·1023/22400 = 2,7·1019 см-3. Толщина атмосферы, приведенная к постоянному давлению в 1 атм, равна примерно h≈10 км. Интенсивность солнечного излучения, прошедшего в атмосфере путь х, равна
32.4. Воспользуемся результатами задач 32.2 и 32.3. Для воздуха n—1=0,000292; при атмосферном давлении число молекул в единице объема N = 6·1023/22400 = 2,7·1019 см-3. Толщина атмосферы, приведенная к постоянному давлению в 1 атм, равна примерно h≈10 км. Интенсивность солнечного излучения, прошедшего в атмосфере путь х, равна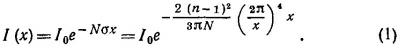
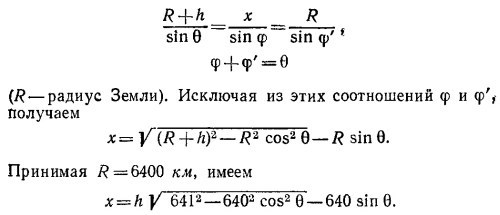

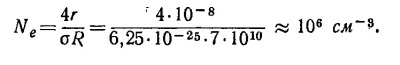
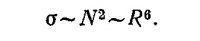
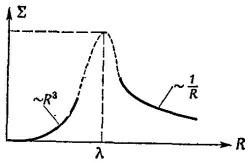 Тогда сечение рассеяния единицей массы ∑= σ·n~R3 (n~ 1/R3—число частиц в единице массы). При R > λ ситуация меняется—внутрь непрозрачной большой частицы свет не попадает, он рассеивается и поглощается лишь атомами, расположенными на поверхности, и суммарное сечение поглощения и рассеяния примерно равно поперечному сечению частицы: σ = πR2, a ∑~1/R. Эта ситуация схематически изображена на рисунке. Значит, эффективность рассеяния единицей массы достигает максимума примерно при R=λ и в этом случае σ ≈лλ2. Для оценки можно воспользоваться этим приближенным соотношением. По условиям задачи Nλx: = ln 100. Искомая масса на единицу площади равна
Тогда сечение рассеяния единицей массы ∑= σ·n~R3 (n~ 1/R3—число частиц в единице массы). При R > λ ситуация меняется—внутрь непрозрачной большой частицы свет не попадает, он рассеивается и поглощается лишь атомами, расположенными на поверхности, и суммарное сечение поглощения и рассеяния примерно равно поперечному сечению частицы: σ = πR2, a ∑~1/R. Эта ситуация схематически изображена на рисунке. Значит, эффективность рассеяния единицей массы достигает максимума примерно при R=λ и в этом случае σ ≈лλ2. Для оценки можно воспользоваться этим приближенным соотношением. По условиям задачи Nλx: = ln 100. Искомая масса на единицу площади равна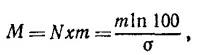
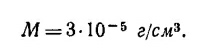
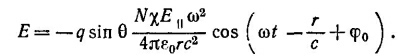
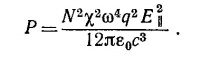
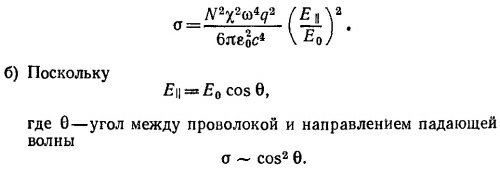
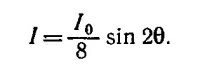
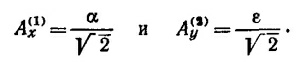
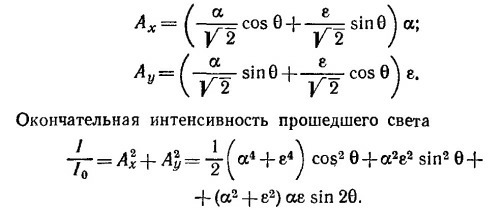
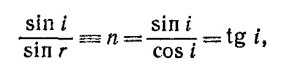
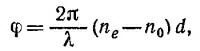
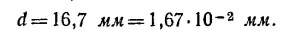
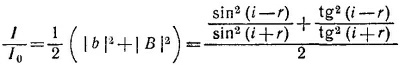
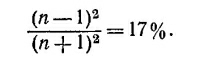
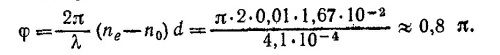
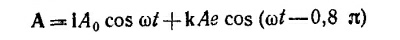
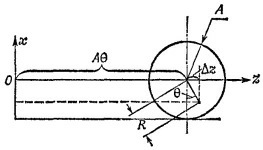 34.1. Перемещение точки по вертикали равно x=–Rcos θ (см, рисунок). Горизонтальное перемещение складывается из поступательного, равного Aθ (диск катится без скольжения), и вращательного, равного Δz = Rsin θ, т. е.
34.1. Перемещение точки по вертикали равно x=–Rcos θ (см, рисунок). Горизонтальное перемещение складывается из поступательного, равного Aθ (диск катится без скольжения), и вращательного, равного Δz = Rsin θ, т. е.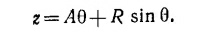
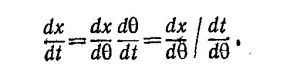

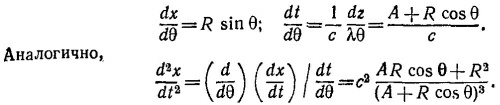
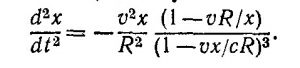
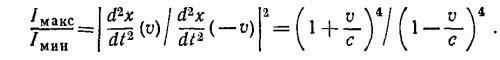
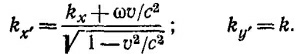
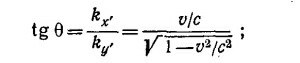
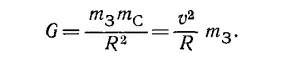
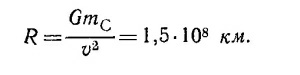
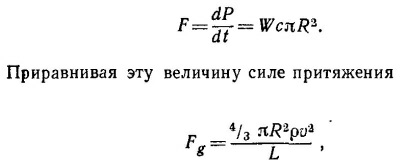
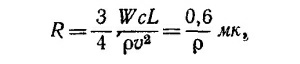
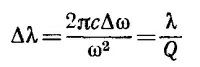
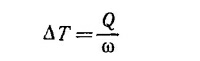
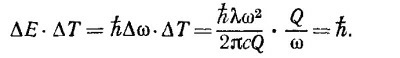
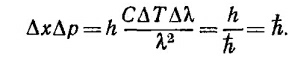
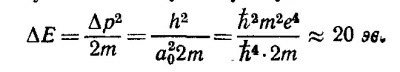
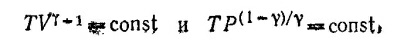
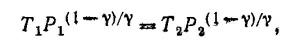
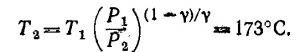
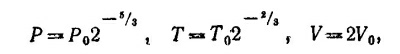
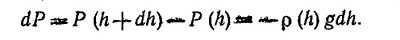
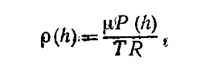
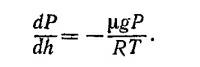
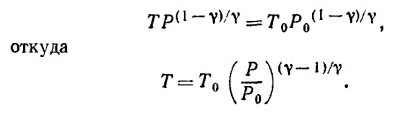
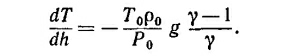
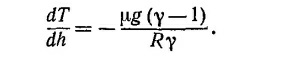

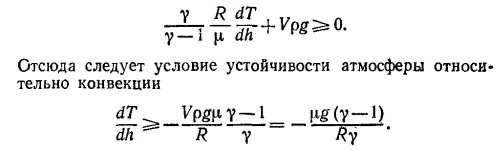
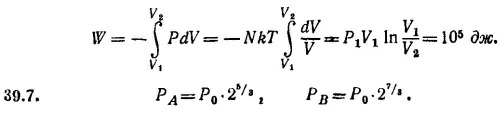
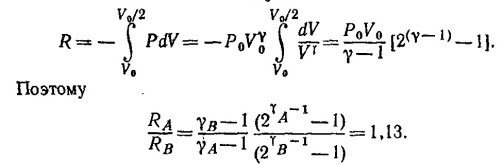
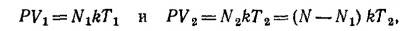
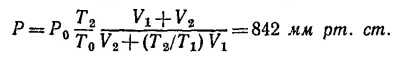
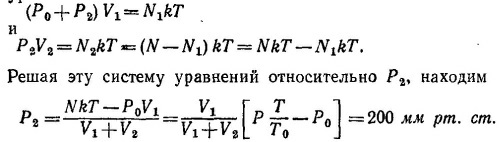
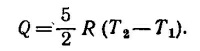
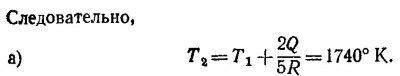
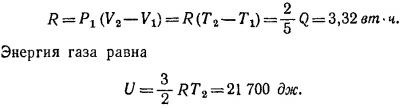
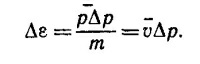
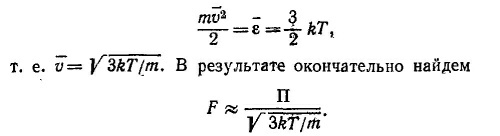
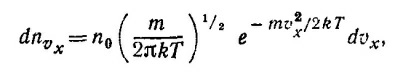
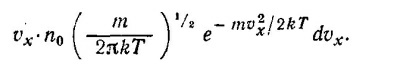
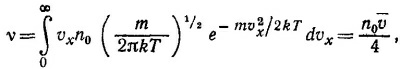

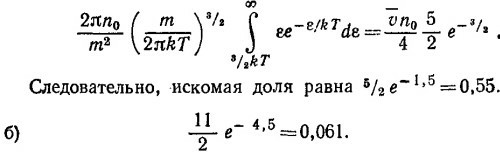
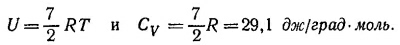
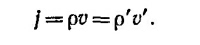
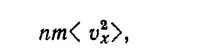
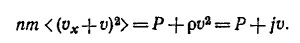
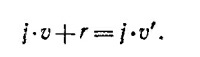
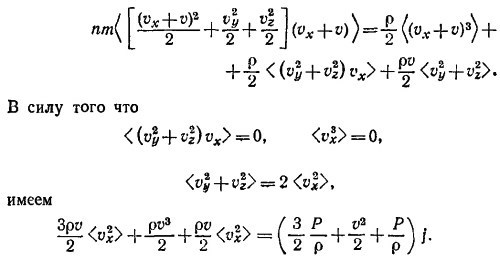
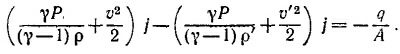

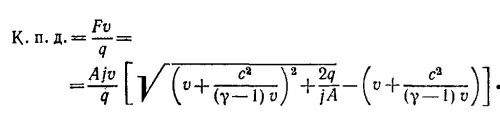
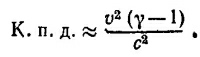
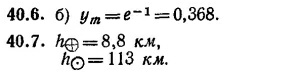

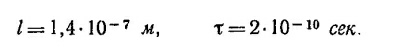
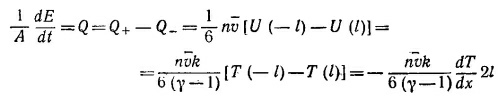
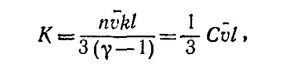
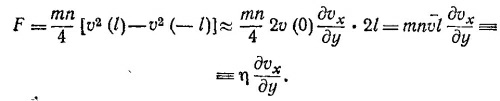
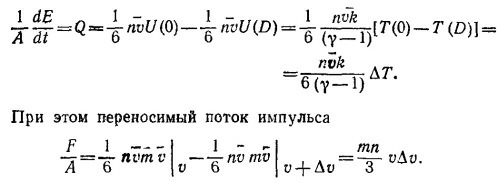
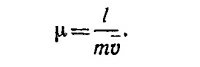

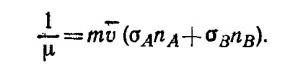
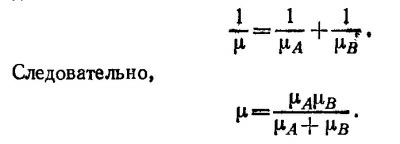
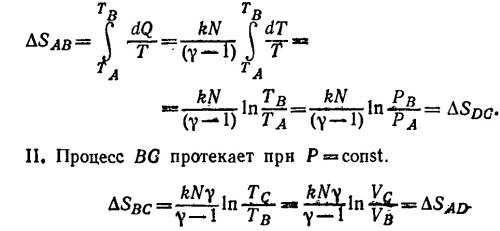

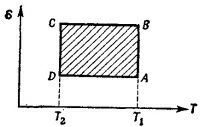 44.2. В силу закона идеального газа
44.2. В силу закона идеального газа
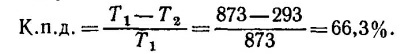
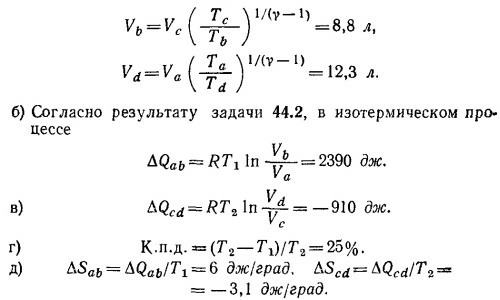
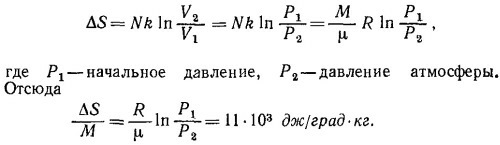
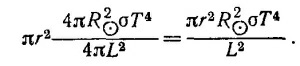
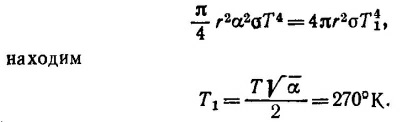
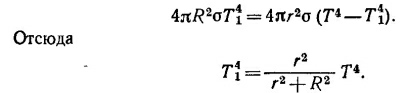
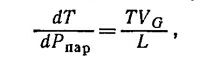
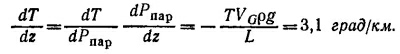
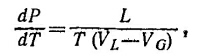
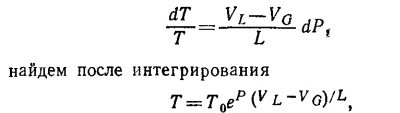
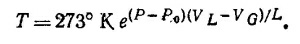
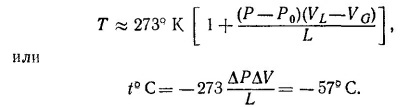
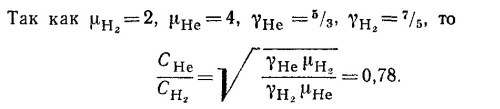
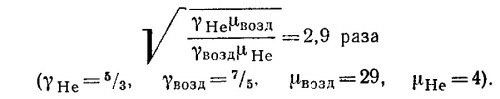
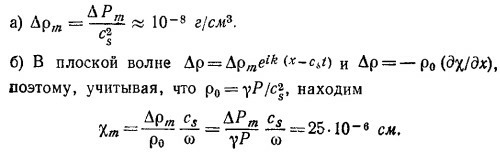
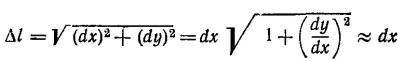
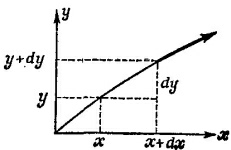 и напишем для него уравнение движения вдоль оси у. Очевидно, масса этого участка равна σdx, а ускорение d2y/dt2. Равнодействующую сил, действующих на выделенный участок, найдем, спроектировав силы натяжения в точках х и x+dx на ось у. На концах отрезка эти проекции равны величине Т, умноженной на синусы углов, которые составляют касательные к струне в этих точках с осью х. В силу малости углов синусы приближенно равны тангенсам этих углов, т. е. dy/dx. Следовательно, равнодействующая сила, действующая на участок струны и направленная в поперечном направлении, равна
и напишем для него уравнение движения вдоль оси у. Очевидно, масса этого участка равна σdx, а ускорение d2y/dt2. Равнодействующую сил, действующих на выделенный участок, найдем, спроектировав силы натяжения в точках х и x+dx на ось у. На концах отрезка эти проекции равны величине Т, умноженной на синусы углов, которые составляют касательные к струне в этих точках с осью х. В силу малости углов синусы приближенно равны тангенсам этих углов, т. е. dy/dx. Следовательно, равнодействующая сила, действующая на участок струны и направленная в поперечном направлении, равна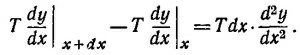
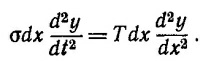
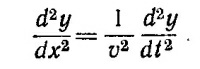
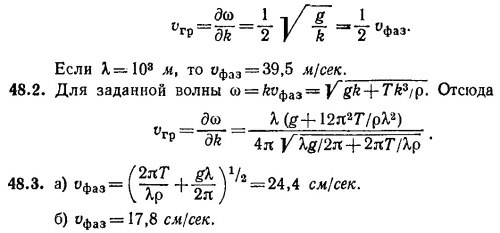

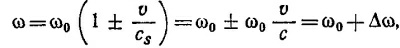
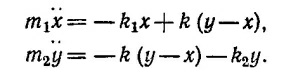
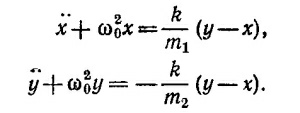
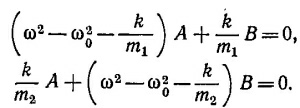
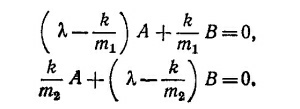
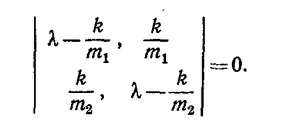
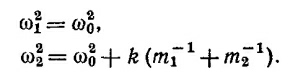
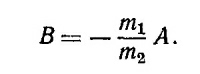
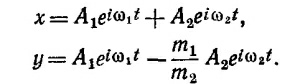
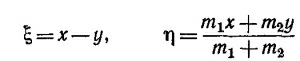

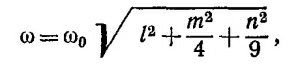
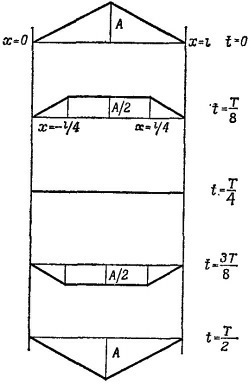 49.5. Пусть f(х) —функция, описывающая начальную форму оттянутой струны, а Т —полный период колебания. Представим себе начальную форму струны как суперпозицию двух горбов, описываемых функциями f(х)/2, движущихся с одинаковой скоростью в противоположных направлениях. Тогда отражение каждого горба от соответствующего закрепленного конца струны можно описать так, как это изложено в § 1 гл. 49 «Лекций» (вып. 4). Найденные таким построением положения струны в момент времени t=0, Т/8, T/4, 3T/8 и Т/2 изображены на рисунке.
49.5. Пусть f(х) —функция, описывающая начальную форму оттянутой струны, а Т —полный период колебания. Представим себе начальную форму струны как суперпозицию двух горбов, описываемых функциями f(х)/2, движущихся с одинаковой скоростью в противоположных направлениях. Тогда отражение каждого горба от соответствующего закрепленного конца струны можно описать так, как это изложено в § 1 гл. 49 «Лекций» (вып. 4). Найденные таким построением положения струны в момент времени t=0, Т/8, T/4, 3T/8 и Т/2 изображены на рисунке.