Главная >> Лекции по ядерной физике

5.6. Спектр замедляющихся нейтронов (спектр Ферми) в гомогенной непоглощающей среде

Игнорируя вывод, приведём конечный вид спектра Ферми (с выводом можно познакомиться, например в [8]).
 
Распределение величины плотности потока замедляющихся нейтронов в непоглощающих средах (имеются в виду свойства не поглощать замедляющи­еся нейтроны, а не тепловые) оказывается подчинённым закономерности:
 
 Ф(Е) = q_f/(ξΣ_sE)        (5.6.1)
 
Это выражение справедливо как для простой однородной среды, так и для сложных гомогенных сред, состоящих их нескольких сортов замедляю­щих ядер. В этом случае в формулу (5.6.1) подставляется сумма значений замедляющей способности k компонентов сложной среды:
                                                                       _k
ξΣ_s = ξ₁Σ_s1 + ξ₂Σ_s2+ ξ₃Σ_s3 + ... + ξ_kΣ_sk = Σ(ξ_iΣ_si)                    (5.6.2)
                                                                      ⁱ⁼¹

Учитывая классическую зависимость кинетической энергии нейтрона от его скорости (Е = mv²/2) и связь плотности потока и плотности нейт­ронов одинаковой скорости
 
Ф(Е) = n(E) v(E) = n(E) √(2E/m) = √(2/m)  n(E)E^1/2,


выражение для спектра замедляющихся нейтронов можно записать так:
                   
 n(E) = q_f √(m/2) /(ξΣ_s E^3/2)                                        (5.6.3)


Таким образом, величина плотности замедляющихся нейтронов по энер­гиям в непоглощающей среде распределяется по закону "Е^-3/2", тоесть плавно возрастает с уменьшением энергии нейтронов в процессе их замедления, и столь же плавно (без скачков и изломов) переходит при Е = Е_с в максвелловский спектр тепловых нейтронов (рис.5.9).

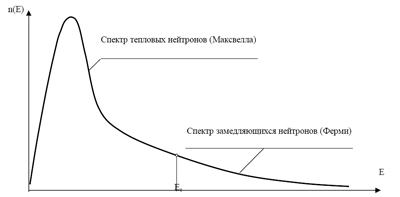Рис.5.9. Граница тепловых и замедляющихся нейтронов - энергия сшивки энергетических спектров Максвелла и Ферми (Е_с).

Уже отмечалось, что об энергетическом спектре нейтронов в реакто­ре имеет смысл говорить только для критического реактора, так как лю­бой энергетический спектр в поглощающей среде имеет динамически-равновесный характер:плотность нейтронов любой энергии Е поддерживается неизменной во времени в любом единичном объёме за счёт неизменной разни­цы скоростей:
 
- прихода замедляющихся нейтронов на уровень энергии Е из области более высоких энергий;
- ухода замедляющихся нейтронов с уровня энергии Е в область бо­лее низких энергий;
- появления в единичном объёме новых нейтронов энергии Е за счёт делений ядер (если таковые имеются в рассматриваемом единичном объёме);
- поглощения нейтронов при энергии Е (если в единичном объёме на­личествуют резонансные поглотители) и
- утечки нейтронов энергии Е из рассматриваемого единичного объё­ма (понимая под утечкой разницу скоростей ухода и прихода нейт­ронов с энергией Е в этом единичном объёме).

В рамках одногруппового возрастного приближения договорились счи­тать, что поглощение в диапазоне энергий замедления отсутствует, а за­метное поглощение замедляющихся нейтронов в реальных средах учитывать с помощью вероятности избежания резонансного захвата (φ). В этом приб­лижении среда активной зоны поглощает только тепловые нейтроны. И если предполагать, что энергетический спектр тепловых нейтронов - максвел­ловского типа, величина и положение максимума на шкале энергий в нём явно должны зависеть от поглощающей характеристики среды (Σ_a) и замед­ляющей способности среды (ξΣ_s) в области энергий перехода от замедляю­щихся нейтронов к тепловым (то есть в области энергии сшивки Е_с) и ни­же (то есть в пределах самого спектра тепловых нейтронов).
 
Действительно, поскольку в тепловой области энергий микросечения поглощения изменяются по закону "1/v" (или"Е^1/2"), то основное погло­щение тепловых нейтронов происходит при более низких энергиях левого крыла спектра Максвелла; чем выше величина микросечения поглощения ак­тивной зоны sa (а значит - и Σ_a), тем больше тепловых нейтронов погло­щается при Е < E_нв, тем больше "выедание" левого крыла спектра, а это значит, что положение максимума спектра (характеризуемое Е_нв - наиболее вероятной энергией тепловых нейтронов) с увеличением поглощающей спо­собности среды должно смещаться вправо, в область более высоких энер­гий; иначе говоря, с увеличением поглощающих свойств среды энергетический спектр тепловых нейтронов ужестчается. Но, т.к. положение макси­мума в спектре тепловых нейтронов определяет температуру нейтронов Т_н (ведь Е_нв= kT_н), то можно выразиться иначе: с увеличением поглощающих свойств среды повышается температура нейтронов в ней. И чем больше величина макросечения поглощения среды (Σa) - тем больше величина температуры нейтронов в ней (Т_н) отклоняется от её термодинамической темпе­ратуры (Т) в сторону увеличения.
 
С другой стороны, чем выше величина замедляющей способности среды (ξΣ_s), тем с большей скоростью пополняется за счёт замедления нейтро­нов весь спектр тепловых нейтронов (в том числе и его левое крыло), и поэтому положение его максимума, наоборот, смещается влево, в область более низких энергий, т.е. с уве­личением замедляющей способности среды спектр тепловых нейтронов умягчается, и температура тепловых нейтронов в среде с лучшими замедляющими свойствами меньше отличается от термодинамической температуры этой среды по сравнению со средой с более слабыми замедляющими свойствами.

Таким образом получается, что температура нейтронов Т_н находится в прямой зависимости от величины Σ_a среды активной зоны и в обратной за­висимости - от ξΣ_s.
 
Это дало повод к предположению, что обе зависимости являются про­порциональными, что дает лёгкую возможность построить полуэмпирические зависимости для расчёта температуры нейтронов в тепловом реакторе:
 
Т_н = Т_з[1 + 1.8 (Σ_a/ξΣ_s)] - для уран-водных гомогенных сред,      и       (5.6.4)
Т_н = Т_з[1 + 0.91(AΣ_a/Σ_s)] - для случаев использованиядругих замедлителей   (с массовым числом A) (5.6.5)
 
Таким образом, температура нейтронов в тепловом реакторе - величи­на, прямо-пропорциональная термодинамической температуре активной зоны и величине, обратной коэффициенту замедления среды в ней.
 
Приведённые формулы получены, строго говоря, для гомогенных смесей топлива и замедлителя, однако, с достаточной точностью могут служить и для оценки температуры нейтронов в гетерогенных активных зонах реакто­ров соответствующих типов, для чего в них должны подставляться средняя термодинамическая температура замедлителя Т_з и величины  гомогенизированных макросечений активной зоны Σ_a и Σ_s.
 
*) Гипотеза насчет пропорциональности Т_н,Т_з и обратного коэффици­ента замедления являлась бы строго-доказательной только в том случае, если бы было строго доказано, что энергетический спектр тепловых нейтронов, как бы ни деформировала его среда своими поглощающими и замедляющими свойствами, всегда сохраняет макс­велловскую форму.

Разговор был посвящен фермиевскому спектру замедляющихся нейтронов, но был смещен к спектру тепловых нейтронов, чтобы подчеркнуть два важ­ных момента:
 
- во-первых, между двумя этими энергетическими спектрами в крити­ческом тепловом реакторе существует какая-то неясная пока взимосвязь: любое, самое малейшее, изменение в спектре тепловых нейтронов обязате­льно должно повлечь за собой изменение и в спектре замедляющихся нейт­ронов, и, наоборот, изменение в фермиевском спектре должно отразиться и на максвелловском распределении тепловых нейтронов;  эту взаимосвязь можно было бы предсказать и без углубленного экскурса в спектры, если просто по-материалистически уверовать в то, что всем поведением замед­ляющихся и тепловых нейтронов управляет одна Среда, только Среда и исключительно Среда; это Она, благодаря присущим ей природным свойствам, единым образом, с единой закономерностью рождает с определенной скоро­стью быстрые нейтроны деления, замедляет их с определенной (связанной со скоростью генерации быстрых нейтронов) интенсивностью, поглощает их с определенной (связанной со скоростями генерации и замедления) скоро­стью, и определяет скорость утечки нейтронов из любого микрообъёма,- и все это природное предопределение свойственно нейтронам любой энергии; иначе говоря, Среда, в силу своих природных свойств, и расставляет все нейтроны по энергиям в единый энергетический спектр, не являющийсяся ни спектром Уатта, ни спектром Ферми и ни спектром Максвелла;
 
- во-вторых, хотя спектры Уатта, Ферми и Максвелла и отражают за­кономерности рождения, замедления и поглощения нейтронов, связать их в единое аналитическое выражение для единого энергетического спектра ре­актора не удаётся, так как спектры Уатта и Максвелла нормированы соот­ветственно на один нейтрон деления и тепловой нейтрон, а спектр Ферми - вообще не является нормированным.
 
Не стоит воспринимать сказанное как критику существующей физичес­кой теории реакторов: скорее, это её очередная проблема, с которой лю­бому человеку, связанному с ядерной энергетикой, следует быть знакомым. Потому что её разрешение радикальным образом изменит не только систему теоретических представлений и облегчит их восприятие: должны открыться новые возможности для быстрых инженерных расчётов и анализа эксплуата­ционной безопасности любых реакторов.
 
Пока же мы вынуждены довольствоваться упомянутой триадой энерге­тических спектров и для расчётов критических свойств реакторов пользо­ваться громоздкими (хотя и приближёнными) вычислениями с помощью ЭВМ.

СМОТРИТЕ ТАКЖЕ: