Главная >> Лекции по ядерной физике 10.2. Условие устойчивости энергетического реактора.
С понятием устойчивости встречаются едва ли не в любой области знаний, особенно - в технических областях человеческой любознательности.
Например, устойчивость корабля (в морской профессиональной терминологии называемая остойчивостью):
Остойчивость корабля - это его способность плавать в прямом ненаклоненном положении, сопротивляться действию внешних сил, стремящихся вывести корабль из этого положения, и возвращаться вновь к этому положению после прекращения действия возмущающих сил.
Представьте себе стоящий на якоре корабль: при отсутствии действия возмущающих сил (при отсутствии дующего в борт ветра) он стоит прямо, без крена; подул слабый ветерок - корабль накренился на небольшой угол в направлении ветра и остался в этом положении, сопротивляясь кренящему моменту; ветер стал дуть сильнее - корабль накренился больше, вновь сохранив устойчивое наклоненное положение (:хорошая конструкция позволяет кораблю создать восстанавливающий момент, противоположный кренящему моменту от ветра и равный ему по величине); главное в этих ситуациях то, что корабль не теряет остойчивости (не опрокидывается); когда же возмущающее внешнее воздействие снимается (ветер стих), - корабль снова приходит в прямое ненаклоненное положение.
Аналогичным свойством обладает и хорошо спроектированный реактор: ему тоже присуща способность длительно работать в критическом режиме (на постоянной мощности) при отсутствии возмущений реактивности, удерживаться в критическом состоянии на новом уровне мощности при возмущениях по реактивности и возвращаться к критическому состоянию на старом уровне мощности после прекращения действия возмущений.
Устойчивостью энергетического реактора называется его способность при случайных возмущениях реактивности постоянной величины переходить в критическое состояние на новом уровне мощности, а после снятия возмущения - возвращаться к исходному критическому состояию на старом уровне мощности.
Рассмотрим, какие процессы происходят в реакторе при нанесении ему возмущения по реактивности постоянной величины, и за счёт чего обеспечивается свойство его устойчивости.
Возьмем для наших рассуждений любой конкретный реактор, характеризуемый определенной кривой ТЭР, например, кривой 3-го типа. Представим себе, что он разогрет до номинальной средней температуры теплоносителя и работает на небольшом постоянном уровне мощности Npo в стационарном (= критическом) режиме, то есть у него kэ = 1, а ρ = 0.
Допустим, что такой реактор получает случайное возмущение по реактивности величиной ρ* (для определённости - положительного знака), которое в дальнейшем не снимается, остается сообщенным реактору. Сообщение реактору ρ* > 0 делает реактор надкритическим, а это значит, что тепловая мощность реактора начинает расти (рис.10.2).
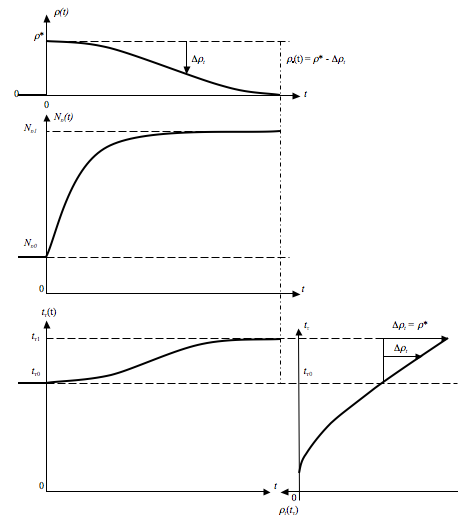
Рис.10.2.Переходные процессы изменений реактивности, мощности и средней температуры теплоносителя при сообщении первоначально критическому реактору положительного возмущения по реактивности.
*) Расположенная в правом нижнем углу кривая ТЭР реактора ради более наглядной согласованности с графиком (в) повернута под 90 градусов. С ростом тепловой мощности реактора при неизменной величине расхода теплоносителя через его активную зону начинает возрастать средняя температура теплоносителя tт (рис.10.2в), что приводит к немедленному появлению температурного изменения реактивности отрицательного знака. По мере роста мощности и средней температуры теплоносителя абсолютная величина отрицательного температурного изменения реактивности нарастает все более и более (рис.10.2г).
Таким образом, в любой момент времени на реактор воздействуют две реактивности разных знаков: ρ* - постоянная во времени сообщенного реактору положительного возмущения и Δρt(tт) - растущая с ростом средней температуры теплоносителя величина отрицательного температурного изменения реактивности, обусловленная ростом с температурой отрицательной величины температурного эффекта реактивности реактора. Реактору безразлично происхождение воздействующей на него реактивности, он подчиняется только суммарной величине воздействующей на него реактивности, которая в данном случае в любой момент времени t с учётом разницы знаков будет равна :
ρΣ(t) = ρ* - Δρt(t)
Следовательно, первоначально положительная величина ρΣ(tо) (равная ρ*) c ростом мощности и средней температуры теплоносителя будет непрерывно уменьшаться, из-за чего скорость нарастания мощности и средней температуры теплоносителя будут также уменьшаться, и в конце-концов настанет такой момент, когда абсолютная величина |Δρt| отрицательного температурного изменения реактивности реактора сравняется с величиной положительного возмущения ρ*, отчего суммарная величина реактивности реактора ρΣ cтанет равной нулю, т.е. реактор вновь станет критическим на достигнутом к этому моменту уровне мощности Np1 при достигнутой к этому моменту средней температуре теплоносителя tт1. Дальнейший рост мощности и средней температуры теплоносителя поэтому прекратится, и режим работы реактора стабилизируется.
Сказанное кратко записывается в виде следующей схемы:

Если в этот момент снять первоначально сообщенное реактору положительное возмущение реактивности ρ*, это равнозначно тому, что критическому (на мощности Np1) реактору сообщается отрицательное возмущение равной величины |-ρ*|, и процессы в реакторе пойдут в обратном порядке: реактор становится подкритическим, его мощность начинает падать, а вместе с ней при постоянном расходе теплоносителя уменьшается средняя температура теплоносителя, из-за чего появляется все более нарастающая величина положительного температурного изменения реактивности; первоначально отрицательная суммарная воздействующая на реактор реактивность увеличивается (или уменьшается по абсолютной величине), и когда нарастающее положительное температурное высвобождение реактивности сравняется с абсолютной величиной |-ρ*|, реактор вновь станет критичным на исходном уровне мощности Npo, а средняя температура теплоносителя в его активной зоне к этому моменту опустится до исходной величины tто.
Теперь вернемся к условию устойчивости реактора. Для приведенных выше рассуждений была взята реальная кривая температурного эффекта реактивности, для которой характерным является ее падающий характер при рабочих средних температурах теплоносителя.
А если бы было по-другому? Если бы кривая ТЭР в зоне рабочих средних температур имела восходящий характер?
- При сообщении реактору положительного возмущения по реактивности рост мощности и связанный с ним рост средней температуры теплоносителя приводил бы к высвобождению за счёт температурных изменений реактивности не отрицательную, а положительную величину реактивности, которая, суммируясь с положительным возмущением ρ*, давала бы ещё большую величину воздействующей на реактор суммарной положительной реактивности, приводя к ещё большей скорости разгона мощности реактора и к ещё большему росту температуры теплоносителя, который вызывал бы еще большее температурное высвобождение положительной реактивности, и т.д., до тех пор, пока активная зона (без вмешательства человека) не разрушится от большого перегрева твэлов реактора. Реактор с такой кривой ТЭР, конечно же, не будет устойчивым реактором.
Следовательно:
Условием устойчивости энергетического реактора является падающий характер его кривой ТЭР в зоне рабочих средних температур тепло- носителя, или (выражаясь теперь более профессионально) – отрица- тельность температурного коэффициента реактивности в этой зоне.
Вот почему, рассматривая формы кривых ТЭР, свойственные энергетическим реакторам, мы не брали в расчёт четвертый (к сожалению, возможный!) тип кривой ТЭР: энергетический реактор с чисто восходящей кривой температурного эффекта реактивности просто не имеет право на существование, поскольку он неустойчив.
Более того, даже реактор с отрицательным ТКР в зоне рабочих температур, будучи принципиально устойчивым, далеко не всегда обеспечивает нужную для дела практическую устойчивость: это зависит, во-первых, от величины отрицательного ТКР, а, во-вторых, от величины возмущающего воздействия ρ*. Какой смысл, к примеру, говорить о принципиальной устойчивости реактора, который при возмущении ρ* = + 0.0015 (или + 0.15%) прекратит увеличение мощности лишь тогда, когда она достигнет 200% от номинальной, а средняя температура теплоносителя вырастет выше 350оС ?! Такой реактор без внешнего вмешательства в его работу (со стороны оператора или системы автоматического регулирования) так же сгорит, как и реактор с положительным ТКР. Следовательно, малый по абсолютной величине отрицательный ТКР явно недостаточен для обеспечения практической устойчивости реактора.
Ладно, предположим, что нам удалось создать реактор с большим по абсолютной величине отрицательным ТКР в зоне рабочих средних температур. В этом случае увеличение средней температуры даже на 2 - 3оС сопряжено с появлением большой температурной отрицательной реактивности, и даже для небольшого увеличения мощности реактора требуется затрачивать для компенсации этой отрицательной реактивности большие величины оперативного запаса реактивности реактора. Значит, и большая абсолютная величина отрицательного ТКР - нехороший фактор, ограничивающий маневренные свойства реакторной установки.
Но и это ещё - полбеды: большой отрицательный ТКР может в определенных обстоятельствах стать источником ядерной опасности. Достаточно представить себе ситуацию, связанную с резким охлаждением активной зоны (обусловленным, например, резким увеличением отбора тепла в парогенераторе, или "забросом" относительно холодной воды в активную зону реактора): в результате резкого снижения средней температуры активной зоны на несколько градусов при большом отрицательном ТКР в реакторе будет высвобождена большая величина положительной реактивности, причём в течение такого малого промежутка времени, за который вводимые в активную зону органы СУЗ (имеющие ограниченную скорость перемещения) не сумеют скомпенсировать высвобождаемую большую положительную реактивность, что может привести к неконтролируемому разгону мощности реактора.
Следовательно, абсолютная величина отрицательного ТКР в рабочей зоне температур должна быть не большой и не малой, она должна быть оптимальной для данного реактора с учётом оперативных возможностей его органов СУЗ, требующейся для практических целей маневренности реакторной установки, располагаемого оперативного запаса реактивности и некоторых других факторов.
И ещё раз стоит подчеркнуть то главное, о чём ни при каких обстоятельства не имеет права забывать оператор РУ: несмотря на обеспечиваемый конструкторами отрицательный ТКР самой оптимальной величины, возможности по обеспечению устойчивости реактора имеют свои ограниченые пределы. Реактор - не ванька-встанька, который способен подняться вертикально после толчка любой силы, поэтому одна из главных задач оператора РУ - в любых обстоятельствах работы реактора исключить толчки реактора большими возмущениями положительной реактивности. В том числе и реактивности, получаемой за счёт быстрых изменений температурного эффекта, поскольку последняя, как мы уже убедились, может иметь большую величину.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|





