Главная >> Лекции по ядерной физике

11.3. Период реактора, период удвоения мощности и их взаимосвязь

Величина   l /δk_э =  Т , обратная величине показателя экспоненциала в решении элементарного уравнения кинетики реактора n(t) = n_o exp (δk_э t / l), называется периодом реактора при заданной величине реактивности.
 
Подобное название обусловлено тем, что, во-первых, эта величина имеет размерность времени, а, во-вторых,  само это название заимствовано из математики, где период экспоненциальной функции является наиболее наглядной её характеристикой. Смысл этой величины применительно к рассматриваемому случаю  можно пояснить следующим образом. Решение элементарного уравнения кинетики реактора  с учётом принятого обозначения периода имеет вид:
 
                                            n(t) / n_o =  exp ( t / T ) ,            (11.17)
 
из которого следует, что за время  t = T  величина плотности  нейтронов в реакторе изменяется в  е = 2.718281... раз  ( при определённой постоянной величине сообщённой реактору реактивности, или, что то же, при постоянной величине избыточного коэффициента размножения δk_э ).
При положительной величине реактивности (ρ > 0) величина периода реактора также имеет положительный знак, при отрицательной величине реактивности  (ρ < 0)  величина периода реактора  отрицательна.

Период реактора является единственной характеристикой для чисто экспоненциального переходного процесса n(t) в реакторе, позволяющей оценивать интенсивность изменения плотности нейтронов или мощности реактора, и при этом является легко воспринимаемой и легко измеряемой величиной. Чем выше величина периода Т, тем менее круто (более плавно) происходит изменение мощности при сообщении критическому реактору реактивности того или иного знака.

Из определения периода следует, что его величина определяется величиной сообщённой реактору реактивности ( или величиной δk_э ). Из этого следует, что при относительно малых значениях реактивности величина периода обратно пропорциональна величине реактивности, причём коэффициентом  пропорциональности
                                                Т ≈ l / ρ                         (11.18)
служит величина среднего времени жизни поколения нейтронов в реакторе l.

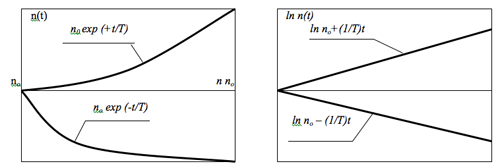
Рис. 11.6. Изображения переходных процессов, вытекающих из решения элементарного уравнения кинетики реактора, в натуральной и полулогарифмической системах координат. Из правого графика следует, что величина, обратная периоду реактора, интерпретируется тангенсом угла наклона к оси абсцисс прямой переходного процесса в полулогарифмических координатах. 

В переходных процессах n(t), которые в соответствии с решением  элементарного уравнения кинетики имеют чисто экспоненциальный вид, величина  Т при  постоянной величине сообщённой критическому реактору реактивности - есть величина постоянная в течение всего времени переходного процесса n(t), а это говорит о том, что и величина среднего времени жизни  поколения  нейтронов (l) - тоже предполагается величиной постоянной в любой момент времени переходного процесса.
Если построить любую из экспонент, даваемых решением ЭУКР,  в полулогарифмической системе координат  ln n(t) = f(t), то экспоненциальный процесс в такой системе координат изобразится прямыми линиями с угловыми  коэффициентами, равными величине обратного периода (1 / T) при любом  знаке  реактивности.    Пара таких экспонент  (возрастающая - при ρ > 0  и  убывающая - при ρ <  0) показаны на рис.11.5.

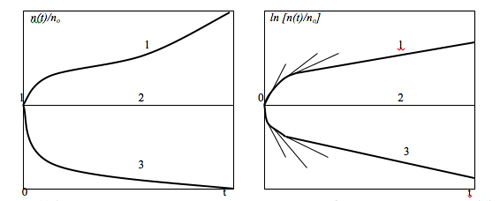
Рис.11.5. Экспоненциальные переходные процессы  n(t)  в натуральной  и полулогарифмической  системах координат (линии 1 соответствуют положительной, линии 2 - нулевой, линии 3 - отрицательной реактивности).

Угловой коэффициент прямой линии (если вспоминать аналитическую геометрию) - это тангенс угла наклона её к оси абсцисс. В более общем случае, применительно к кривым линиям, тангенс угла наклона касательной в точке кривой линии - интерпретируется как значение первой производной функции,  описывающей эту линию, в этой точке.
Поэтому, если прологарифмировать по точкам график переходного процесса в реальном реакторе (о котором говорилось в п.11.1.1), становится ясным, что величина периода реактора будет примерно постоянной только в развитой  части переходного процесса, а на стадии начального скачка величина периода   реактора - переменна.

Приходится признать, что на первой стадии переходного процесса n(t), то есть на стадии начального скачка, при постоянной величине реактивности  (или δk_э)  переменной величиной является величина среднего времени жизни поколения нейтронов.  За счёт  чего? - Очевидно, за счёт того, что в течение начального скачка переменной величиной является соотношение  скоростей генерации мгновенных и запаздывающих нейтронов.
 
Величина периода реактора Т, являясь удобной аналитической характеристикой интенсивности переходного процесса n(t) в реакторе,   для практика-оператора реакторной установки не очень удобна с точки зрения её практического измерения.   Представим себе,  как это делается:  в определённый момент переходного процесса, когда стрелка измерителя нейтронной мощности проходит определённое деление на его шкале, включается секундомер, который должен быть остановлен в тот момент, когда стрелка прибора будет показывать значение нейтронной мощности, в 2.71828...раза превосходящее значение при включении секундомера; в этом случае секундомер как раз и покажет величину периода реактора Т. Оператору для измерения величины периода необходимо знать, на каком делении следует остановить секундомер, для чего он должен выполнить быстрое вычисление: величину начальной нейтронной мощности умножить на число е = 2.7182818.., что, конечно, можно проделать при наличии калькулятора, но “в уме” такое вычисление явно затруднительно.
Поэтому операторы пользуются более практичной характеристикой,  пропорциональной величине периода реактора Т  и называемой периодом удвоения мощности реактора ( Т₂), которая, как следует из её названия, представляет собой время изменения нейтронной  мощности реактора в два раза.  Взаимосвязь величин Т₂  и Т (при одной и той же величине сообщаемой реактору реактивности ρ) вытекает из того же решения ЭУКР. Если в него подставить значение  t = T₂ , то отношение  n(T₂) / n_o = 2  (как следует из определения ), и, следовательно
               2 = exp ( T₂ / T ),   или  Т₂ / T = ln 2 ≈ 0.693, откуда следует, что
 
                 Т₂ ≈ 0.693 Т,  или, наоборот,  Т ≈ 1.44 Т₂             (11.19)
 
И последнее. Элементарное уравнение кинетики реактора и его решение, несмотря на простоту, неплохо служит в прикладном плане, давая возможность непосредственно измерять мгновенное значение периода реактора или периода удвоения его мощности, а, точнее, указывает путь к реализации периодомера - прибора для измерения величины периода. Если в  выражение элементарного уравнения кинетики подставить величину периода реактора  Т = l / δk_э, то получается
      dn /dt = n / T,    откуда следует,   что   Т = (dn / dt) / n(t),             (11.20)    
                                                  то есть:
Мгновенное значение величины периода реактора есть отношение производной изменения плотности нейтронов в реакторе  к  мгновенному значению самой величины плотности нейтронов.

Нейтронная  мощность реактора измеряется, как известно, с помощью нейтронных камер, по величине  электрического тока камер, пропорциональной величине измеряемой нейтронной мощности реактора. Из последней формулы для Т вытекает, что для измерения мгновенного значения величины периода реактора Т(t) следует выходной сигнал ионизационных камер:
- продифференцировать (в дифференцирующем блоке);
- получить его обратную величину (в конвертирующем блоке);
- подать выходные сигналы с этих двух блоков на блок перемножения, в котором получается сигнал, пропорциональный их произведению (и пропорциональный величине периода реактора Т);
- пропустить этот сигнал через масштабирующий блок с коэффициентом 0.693 для получения электрического сигнала, пропорционального величине периода удвоения мощности реактора Т₂ и подать полученный сигнал на показывающий электроизмерительный прибор.

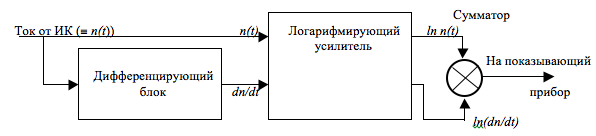
Рис. 11.6. Принципиальная  блок-схема измерителя периода удвоения мощности реактора.

Краткие выводы 
Кинетика реактора - раздел теории, изучающий и описывающий закономерности изменения во времени плотности нейтронов в реакторе при ненулевых реактивностях.
 
В кинетическом описании переходных процессов существенную роль играет величина  времени жизни поколения нейтронов в реакторе.
 
Элементарное уравнение кинетики реактора ,  которое не учитывает различий между мгновенными и запаздывающими нейтронами, не даёт полного объяснения закономерного характера переходных процессов n(t) в реальных реакторах при сообщении им реактивности. Его решение объясняет лишь экспоненциальную стадию в развитой части переходных процессов, но не даёт объяснения наличию в реальных переходных процессах стадии начального скачка плотности нейтронов, с которой начинается переходный процесс n(t).    Это вынуждает заниматься более детальным изучением закономерностей генерации нейтронов в реакторе и выделять среди них запаздывающие нейтроны.
 
Запаздывающие нейтроны  получаются за счёт выхода при делении ядер топлива тринадцати основных  типов потенциально нейтроноактивных осколков  деления, называемых предшественниками запаздывающих нейтронов.  Предшественники, испытывая первым β-распад, в качестве дочерних продуктов этого распада дают нейтроноактивные  излучатели запаздывающих нейтронов, из которых и испускаются запаздывающие нейтроны.
 
Отличия запаздывающих нейтронов, испускаемых различными излучателями, заключаются в различных величинах их начальной кинетической энергии и их абсолютными долями выхода, а также величинами времени запаздывания.  Для более компактного описания тринадцать типов запаздывающих нейтронов объединены в шесть групп по принципу близости их основных характеристик. Эти шесть групп характеризуются усреднёнными значениями долей выхода, постоянных β-распада и начальной энергии.  Средняя начальная кинетическая энергия запаздывающих нейтронов всех шести групп равна 0.49 МэВ, а суммарная доля выхода в общем балансе генерации нейтронов для запаздывающих нейтронов в критическом реакторе бесконечных размеров равна 0.0064 (для ²³⁵U) и 0.0021 (для ²³⁹Pu).  В реальном уран-плутониевом топливе энергетических реакторов усреднённая величина доли выхода запаздывающих нейтронов в процессе кампании активной зоны снижается пропорционально уменьшению содержания ²³⁵U  в топливе. В реакторах АЭС величина эффективной доли выхода запаздывающих нейтронов  уменьшается от 0.0064  (для свежего топлива в начале кампании) до 0.0045 - 0.0050 (в конце кампании). В реакторах больших размеров (реакторах АЭС) величины теоретической и эффективной долей выхода запаздывающих нейтронов приблизительно равны (величина ценности запаздывающих нейтронов в этих реакторах близка к единице).
 
Роль запаздывающих нейтронов состоит в том, что относительно небольшое их количество в реакторе увеличивает  значение  среднего  времени жизни поколения нейтронов как минимум на три порядка величины (от  ~10 ^-4 до ~ 10 ^-1 с), благодаря чему  и реализуется возможность безопасного управления реактором.
 
Характеристиками интенсивности развития  экспоненциальных переходных  процессов  n(t)  в реакторах являются период реактора и период удвоения мощности. Последняя характеристика для практика более удобна из-за простоты её “безоружного” измерения. Эти две характеристики пропорционально взаимосвязаны друг с другом зависимостью:
                              T₂  ≈ 0.693 Т ,   или   Т ≈ 1.44 Т₂
Математической интерпретацией мгновенного значения изменяющегося  периода Т  является отношение мгновенных значений производной плотности нейтронов  и самой величины плотности нейтронов в реакторе.

СМОТРИТЕ ТАКЖЕ: