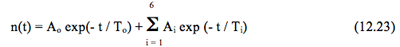Главная >> Лекции по ядерной физике >> Переходные процессы при сообщении реактору отрицательной реактивности

12.2.1. Характер переходных процессов n(t) при ρ < 0.

Так как при сообщении реактору отрицательной реактивности все семь корней уравнения обратных часов отрицательны, это означает, что общее решение системы дифференциальных уравнений кинетики представляет собой алгебраическую сумму убывающих экспонент (любая экспонента с отрицательным показателем - убывающая). А поскольку (см. условие (12.22)) все без исключения постоянные интегрирования  А_i в случае отрицательной реактивности положительны, то можно выразиться более точно: при отрицательной реактивности решение системы дифференциальных уравнений кинетики есть арифметическая сумма семи убывающих экспонент, и если обозначать  через Т_i абсолютную величину корней уравнения обратных часов, то:

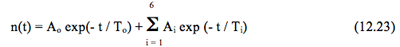
Геометрическое суммирование семи убывающих экспонент показано на рис.12.2. Как видим, переходный процесс n(t) в “холодном” реакторе имеет уже не тот моноэкспоненциальный вид, который получался из решения элементарного уравнения кинетики: здесь хорошо просматриваются две стадии развития переходного процесса, свойственные реальным переходным процессам во всех реакторах, а именно, - стадия  начального скачка, продолжительность которой определяется временем, в течение которого шесть младших экспонент спадают до практического нуля, и стадия чисто экспоненциального спада плотности нейтронов, определяемая старшей, экспонентой  А_о exp (- t / T_o), показатель которой обратно пропорционален наибольшему по абсолютной величине корню уравнения обратных часов.

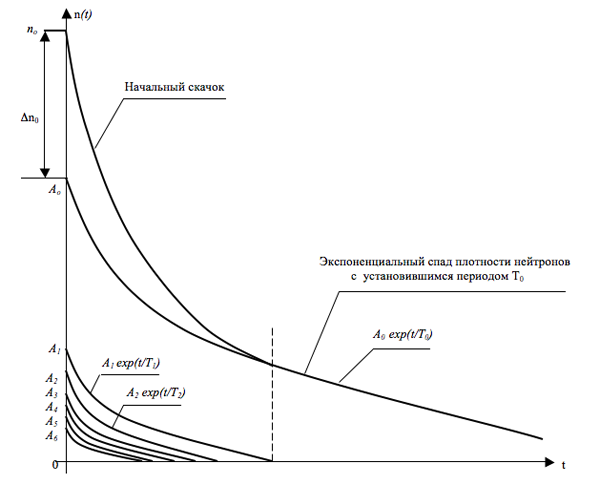
Рис.12.3. Экспоненциальные составляющие переходного процесса n(t) при скачкообразном сообщении критическому реактору отрицательной реактивности.

Теперь смысл названия установившегося периода Т_о должен быть окончательно ясен.

Зависимость любого (переходного) периода Т_i при отрицательной величине сообщаемой реактору реактивности имеет обратный характер: чем больше абсолютная величина сообщаемой реактору отрицательной реактивности, тем меньше абсолютная величина любого из корней уравнения обратных часов Т_i (что очень наглядно иллюстрирует график решения уравнения обратных часов). Следовательно, крутизна переходных процессов n(t) в реакторе определяется только величиной сообщаемой реактору отрицательной реактивности: чем больше абсолютная величина отрицательной реактивности, тем более круто идёт спад плотности нейтронов n(t), причём, и на стадии начального скачка, и на стадии последующего экспоненциального спада.

Можно сказать и иными словами: чем больше абсолютная величина сообщаемой реактору отрицательной реактивности, тем больше абсолютная величина начального скачка.

Нелинейный характер начальной стадии переходного процесса ещё более наглядно иллюстрируется  графиком зависимости, построенным в полулогарифмической системе координат для различных значений отрицательной реактивности.(рис.12.4):

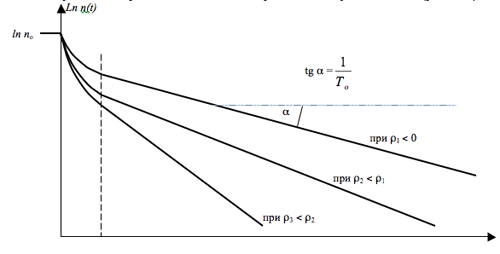
Логарифмирование экспоненциальной функции даёт, как известно, линейную зависимость, изображаемую прямой линией, угловой коэффициент которой численно равен постоянному сомножителю в показателе экспоненты, то есть, в данном случае, - величине (- 1 / Т_о). Поэтому в полулогарифмической системе координат прямой линией изображается только вторая, чисто экспоненциальная, стадия переходного процесса n(t), а на стадии начального скачка переходный процесс выглядит нелинейно.
Наличие стадии начального скачка в переходном процессе n(t) физически объясняется тем, что при скачкообразном сообщении критическому реактору отрицательной реактивности первыми всегда реагируют на это возмущение мгновенные нейтроны: резко уменьшается скорость генерации и резко возрастает скорость их поглощения. И если бы к моменту введения отрицательной реактивности в реакторе не были бы накоплены достаточно большие стационарные концентрации предшественников запаздывающих нейтронов всех групп, процесс начального спада n(t) происходил бы во много раз быстрее (поскольку время жизни мгновенных нейтронов во много раз меньше времени жизни запаздывающих нейтронов любой группы), то есть это был бы практически безынерционный бросок n(t) вниз, почти синхронно отслеживающий уменьшение величины коэффициента размножения на мгновенных нейтронах. Но предшественники запаздывающих нейтронов в реакторе есть, и их стационарные концентрации в критическом реакторе достаточно высоки, а это значит, что в первые секунды начального скачка достаточно высоки и скорости их β-распада (вспомните: dC_i/dt = - λ_iC_i), а, значит, вначале  высоки и скорости генерации запаздывающих нейтронов всех групп, и получается, что эти добавки запаздывающих нейтронов в общий цикл размножения тормозят общее падение плотности нейтронов n(t), которое без них было бы очень резким.
Но поскольку с уменьшением n(t) синхронно уменьшается и скорость деления ядер топлива, то с той же синхронностью уменьшается и скорость генерации предшественников запаздывающих нейтронов всех групп, а с некоторым запаздыванием - и скорость генерации излучателей запаздывающих нейтронов. Скорость уменьшения концентраций ядер-предшественников запаздывающих нейтронов не может стать ниже скорости их β-распада (равной λ_iC_i(t)). Следовательно, экспоненциальный процесс снижения концентрации предшественников каждой группы (надеюсь, вы не сомневаетесь, что он чисто экспоненциальный: ведь решения 6 уравнений для концентраций были найдены в виде C_i(t) = C_oi exp(-t / T_i) ) не может идти с периодом, меньшим, чем период распада предшественников каждой группы (равным 1 / λ_i). Поэтому понятным становится и физический смысл величины переходного периода Т_i: это - периоды экспоненциальных процессов С_i(t), описывающих переходы величин концентраций предшественников запаздывающих нейтронов от одного стационарного значения (С_оi) до другого (соответствующего концу переходного процесса n(t). В частности, судя по виду решения, конечной концентрацией предшественников запаздывающих нейтронов может быть и нулевая их концентрация.
 
Примечание. Обратим внимание с самого начала на эту “несуразицу”: при любом значении сообщаемой реактору отрицательной реактивности концентрации предшественников запаздывающих нейтронов устремляются к нулю, то есть, в соответствии с известным правилом, через (4 ÷ 5) периодов Т_i величины концентраций С_i должны обратиться в практический ноль. Объяснение этому будет дано при рассмотрении кинетики подкритического реактора с независимым источником нейтронов.
 
И лишь тогда, когда скорость снижения n(t) ”вплотную” снизится до скорости β-распада предшественников самой долгоживущей (первой) группы, переходный процесс n(t) плавно переходит во вторую (чисто экспоненциальную) стадию уменьшения плотности нейтронов с установившимся периодом Т_о.

СМОТРИТЕ ТАКЖЕ: