Главная >> Лекции по ядерной физике

13.3. Переходные процессы при изменениях степени подкритичности реактора

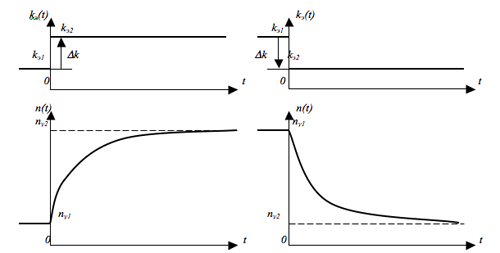
Принципиально нам уже понятно, что переходный процесс в подкритическом реакторе при изменении степени подкритичности реактора от одного значения до другого должен быть процессом перехода  величины плотности нейтронов n(t) от одного установившегося значения n_у1, соответствующего величине начальной степени подкритичности δk_п1, до другого установившегося значения n_у2, соответствующего другому значению степени подкритичности δk_п2.  Поэтому единственное, что нас интересует сейчас, это характер этого переходного процесса, то есть математическая закономерность, которой подчиняется переходный процесс.

Пусть вначале реактор был подкритичен при степени подкритичности δk_п1, в результате чего в нём установилась плотность нейтронов n_у1 = s l / δk_п1. При скачкообразном увеличении степени подкритичности от δk_п1 до δk_п2 на величину Δδk_п = δk_п2 - δk_п1 (что равносильно уменьшению величины эффективного  коэффициента размножения нейтронов на ту же величину: Δδk_п = (1 - k_э2) - ( 1 - k_э1) = - (k_э2 - k_э1) = - Δk) переходный процесс n(t) будет происходить уже при постоянной величине степени подкритичности δk_п2 = δk_п1 + Δδk_п = δk_п1 - Δk, поэтому элементарное уравнение кинетики для этого переходного процесса будет выглядеть как
dn / dt = - ( δk_п2 / l) [ n(t) - (sl /δk_п2)] ,  или  dn / dt = - (δk_п2 / l) [n(t) - n_у2]          (13.9)
Уравнение (13.9) - уравнение с разделяющимися переменными:
                             dn / [n(t) - n_у2] = - (δk_п2 / l ) dt                                                   (13.10)
Решение его следует выполнять при очевидном начальном условии:
                                 при t = 0     n(t=0) = n_у1                                                         (13.11)
Интегрирование даёт следующее:
ln [n(t) - n_у2] = - (δk_п2 / l) t,  а подстановка начального условия в это выражение:
 
  ln {[n(t) - n_у2] /(n_у1 - n_у2)} = - (δk_п2 / l) t,    или [n(t) - n_у2] / (n_у1 - n_у2) = exp [- (δk_п2 / l) t ], откуда:
                                n(t) = n_у2 - (n_у2  - n_у1) exp [- (δk_п2 / l) t ],  или:
                              n(t) = n_у2{l - [1 - (n_у1/ n_у2)] exp [- (δk_п2 / l) t] }                       (13.12)

Учитывая, что отношение начальной и конечной плотностей нейтронов n_у1 / n_у2 = (sl /δk_п1) / (sl / δk_п2) = δk_п2 / δk_п1 = (δk_п1+ Δδk_п) / δk_п1 = 1 - Δk/δk_п1,
 (13.12) можно преобразовать к виду, в котором в правой части фигурируют только исходные данные (n_у1) и величина вносимого изменения степени подкритичности или, лучше, величина изменения эффективного коэффициента размножения Δk = k_э2 - k_э1, соответствующая задаваемому изменению степени подкритичности ( Δk = - Δδk_п):
 
            n(t) =  [n_у1 /(1 - Δk/δk_п1)] {1 + (Δk/ δk_п1) exp [- (δk_п1- Δk) t /l]}.             (13.13)
 
Наконец, выражение для переходного процесса станет ещё прозрачнее, если выразить величины степени подкритичности δk_п1 через величину эффективного коэффициента размножения k_э1:
 
      n(t) = {n_у1 /{1 – [Δk /(1 - k_э1)] }} {1 + [Δk /(1 - k_э1)] exp [(k_э1 - 1 + Δk) t / l]}.      (13.14)
 
Выражение (13.14) однозначно свидетельствует о том, что переходный процесс в подкритическом реакторе при изменении величины эффективного коэффициента размножения на величину Δk (или, что то же, - при изменении степени подкритичности реактора) имеет чисто экспоненциальный характер - возрастающий при увеличении эффективного коэффициента размножения на Δk (или уменьшении степени подкритичности на Δk) и убывающий с уменьшении величины эффективного коэффициента размножения  на Δk (или увеличении степени подкритичности на Δk).
Качественный вид переходных процессов при скачкообразном (ступенчатом) изменении величины эффективного коэффициента размножения  в положительную и отрицательную стороны показан на рис.13.2.

Рис.13.2. Экспоненциальный характер переходных процессов n(t) в подкритическом реакторе: а) при скачкообразном  уменьшении степени подкритичности реактора (или увеличении эффективного коэффициента размножения  на ту же величину)  и  б) при скачкообразном увеличении степени подкритичности реактора (или соответствующем уменьшении величины k_э на ту же величину).

СМОТРИТЕ ТАКЖЕ: