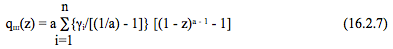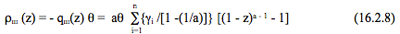Главная >> Лекции по ядерной физике

16.2. Кинетика роста потерь реактивности за счёт шлакования.

Общий вид дифференциального уравнения шлакования реактора одиночным (i-м) шлаком определяется логикой скорости изменения концентрации этого шлака: скорость изменения концентрации любого  шлака - есть разница скоростей его образования (как непосредственного осколка деления ядер топлива) и исчезновения (в результате поглощения нейтронов):
                    dN_i /dt = γ_i σ_f⁵ N₅(t) Ф(t) - σ_aⁱ N_i(t) Ф(t)                                      (16.2.1)
 
Нам интересен наиболее близкий к практике эксплуатации случай работы реактора на постоянном уровне мощности  N_p(t) = idem , условие которого в соответствии с формулой (15.1.3):
                        N₅(t) Ф(t) = idem = N_p / C_N                                                       (16.2.2)                     

Более того, нам уже известен характер изменения плотности потока нейтронов при постоянном уровне мощности реактора Ф(t) = N_p / C_N N₅(t) и характер спада концентрации ²³⁵U в процессе кампании  N₅(W) = N_5o - (σ_a⁵/C_N) N_pt = N_5o - (σ_a⁵/C_N)W (через энерговыработку W), или  N₅(z) = N_5o(1 - z) (через величину степени выгорания z), поэтому выражение для изменяющейся в процессе кампании плотности потока нейтронов в наиболее удобном и общем виде при постоянстве мощности реактора будет:
                                   Ф(t) = N_p / C_NN_5o(1 - z)                                                   (16.2.3)

Для эксплуатационника дифференциальное уравнения шлакования (16.2.1)  нагляднее во всех отношениях решать в эксплуатационных величинах (мощность, степень выгорания топлива), а не в величинах (плотность потока нейтронов, время). Для этого производную по времени dN_i/dt следует заменить производной по степени выгорания dN_i/dz, пользуясь известной взаимосвязью величин.
Так как z = (σ_a⁵/N_5oC_N)N_pt, то dz/dt = (σ_a⁵/N_5oC_N)N_p (величины перед t при постоянном уровне мощности реактора - постоянны), и производная dN_i/dt очевидно будет равна:
              dN_i/dt = (dN_i/dz)(dz/dt) = (σ_a⁵/N_5oC_N) N_p (dNi/dz)                          (16.2.4)
 
Подстановка выражений (16.2.1), (16.2.2) и (16.2.3) в уравнение (16.2.4) даёт следующее:
          dN_i/dz = γ_i f₅N_5o -  [(σ_aⁱ/σ_a⁵) /(1 - z)] N_i(z) .                         (16.2.5)

Примечание.  В процессе подстановки величина сечения деления  урана-235 заменена через сечение поглощения урана-235:  σ_f⁵ = f₅ σ_a⁵ . (Величина доли делящихся ядер урана-235 среди всех поглощающих тепловые нейтроны f₅ ≈ 0.857, если не учитывать различную степень отклонения этих сечений от закона «1/v»).
 
Обозначая для краткости γ_i f₅ N_5o = A, а f₅ = a, получаем дифференциальное уравнение типичного линейного вида:
                       Ni`(z) + [a /(1 -z)] Ni(z) - A = 0
 
Его решение при нулевых начальных условиях (при t = 0 и z =0  N_i(z) = 0, так как в начале кампании концентрация любого шлака в реакторе равна нулю) имеет вид:
 
                        N_i(z) = [(γ_i a N_5o)/(1 – a)](1 - z) [(1 - z) ^{a - 1} - 1]                      (16.2.6)
 

То есть, переходный процесс нарастания концентрации любого (i-го) шлака в реакторе в процессе кампании в зависимости от степени выгорания имеет сложный степенной характер, крутизна которого определяется только величиной начальной концентрацией урана-235 (N_5o).
 
Переходя к другой характеристике процесса шлакования i-м шлаком - доле поглощения нейтронов i-м шлаком - по формуле  q_шi(z) = [(σ_aⁱ/σ_a⁵N₅(z)] N_i(z), - имеем:
q_шi(z) = [a γ_i N_5oσ_aⁱ/σ_a⁵(1 – a)N₅(z)] (1 - z) [(1 -z)^{a - 1} - 1] ,  а так как N₅(z)/N_5o = 1 - z, то:
q_шi(z) = [aγ_iσ_aⁱ/σ_a⁵(1 – a)] [(1 - z) ^{a - 1} - 1] ,  или
q_шi(z) = [aγ_iσ_aⁱ /(σ_a⁵ - σ_aⁱ)] [(1 - z)^{a - 1} - 1] , или, наконец,
q_шi(z) = {aγ_i/[(1/a) - 1]} [(1 - z)^{a - 1} - 1]                              (16.2.6)
 
Это касается только одиночного (i-го) шлака. Для всех же шлаков, взятых вместе, относительная доля поглощаемых ими нейтронов, в соответствии с (16.2):

Но эксплуатационника интересует даже не эта теоретическая величина, а в большей степени - потери реактивности за счёт шлакования, которые, как упоминалось ранее, находятся по формуле (16.3):

Из (16.2.8) следует, что переходный процесс нарастания потерь реактивности в процессе кампании в зависимости от степени выгорания ( z ) представляет собой      сумму n степенных функций (n - число типов шлаков), каждая из которых имеет свою крутизну, определяемую только типом шлака, поскольку величины γ_i и σ_aⁱ (входящие в отношение a = σ_aⁱ/σ_a⁵ - присущи каждому конкретному шлаку, - то есть, иначе говоря, определяемую соотношением микросечений поглощения каждого шлака и урана-235.

По предложению Иоффе и Окуня (1945 г.) вся компания из более чем 60 образующихся при делении шлаков была заменена суммой трёх групп шлаков, каждая из которых имеет усреднённые характеристики.

Если  группа состоит из m шлаков, имеющих достаточно близкие величины физических характеристик (γ_i и σ_аⁱ), то эти характеристики для группы могут быть усреднены по принципу:

а) Удельный выход группы шлаков - есть сумма удельных выходов каждого из шлаков, составляющих группу, то есть:     

б) Средняя величина микросечения поглощения группы - есть средневзвешенное значение микросечений поглощения шлаков, составляющих группу:

Почему именно три группы шлаков? -  Для ответа на этот вопрос надо понять, какие это группы шлаков и чем они качественно отличаются друг от друга.
 
а) Первая группа шлаков (так называемые сильные шлаки)  характеризуется величиной микросечения поглощения составляющих группу шлаков, существенно большей величины микросечения поглощения ²³⁵U:
                                                     (σ_aⁱ)_1гр >> σ_a⁵
Понятно, что величина показателя степенной функции такого шлака - большая величина, и (с точки зрения математика) степенная функция с очень большим по абсолютной величине отрицательным показателем быстро достигает своего асимптотического (в данном случае, нулевого) значения, а  величина [(1- (1/a))((1 – z)^{a –1} – 1)] быстро достигает своего стационарного значения. Физически это означает, что концентрация каждого из шлаков первой группы быстро достигает своего стационарного значения и в дальнейшем не изменяется. Поэтому в основное время кампании активной зоны ( при z ≥ 0.03) можно считать потери реактивности от шлакования реактора шлаками первой групп постоянными и равными приблизительно
 
                                           ρ_ш1гр ≈ - 0.0151 θ.                                            (16.2.11)
 
б) Вторая группа шлаков, характеризуемых величиной микросечения поглощения, по порядку величины совпадающего с сечением поглощения урана-235:
                                                  σ_aⁱ ~ σ_a⁵                                                    
Концентрации шлаков этой группы, растущие в процессе кампании, строго говоря, по степенному закону, в пределах имеющих физический смысл величин степеней выгорания (z < 1) растут настолько медленно, что при реальных величинах степени выгорания урана-235 характер роста потерь запаса реактивности от шлакования реактора шлаками этой группы без особого ущерба для точности можно считать не степенным, а линейным относительно z:
 
                                        ρ_ш2гр ≈ - 0.0414 z θ                                                (16.2.12)
причём, в течение всей кампании.

_σaⁱ  <<  σ_a⁵
Шлаки третьей группы имеют в подавляющем большинстве очень небольшие величины удельного выхода (γ_i), но это - самая многочисленная группа шлаков, и этим объясняется их влияние на общую величину потерь реактивности от суммарного шлакования. Степенные функции нарастания концентраций этих шлаков (и потерь реактивности за счёт шлакования реактора этими шлаками) возрастают гораздо медленнее, чем экспоненты шлаков второй группы, они практически неотличимы от прямых линий, и поэтому с приемлемой  точностью описываются линейной зависимостью:
 
                                        ρ_ш3гр ≈ - 0.0114 z θ                                               (16.2.13)

Качественный характер изменения потерь запаса реактивности от шлакования реактора шлаками каждой из групп, а также суммарная кривая потерь запаса реактивности от шлакования реактора всеми шлаками этих групп показаны на рис.16.1.

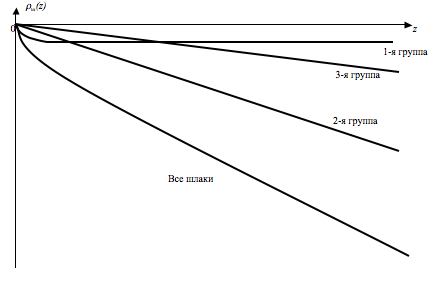
Рис. 16.1. Качественный характер нарастания потерь запаса реактивности за счёт раздельного шлакования реактора шлаками трёх групп и кривая суммарных потерь запаса реактивности от шлакования реактора всеми шлаками.

Эта кривая потерь запаса реактивности от шлакования для любого конкретного реактора может быть пересчитана в кривую зависимости от энерговыработки реактора W, которая, понятно, в рассмотренном случае является величиной, пропорциональной степени выгорания.
Таким образом, главный практический вывод из всего рассмотренного по вопросу шлакования  реактора, который будущему оператору нелишне запомнить, таков:
Потери запаса реактивности реактора от шлакования в процессе кампании в зависимости от энерговыработки (или степени выгорания урана-235) лишь в самый начальный период кампании (< 5% от номинальной энерговыработки реактора) нарастают нелинейно, что объясняется относительно быстрым ростом концентрации каждого из сильных шлаков до их стационарных концентраций. В оставшийся период кампании они растут практически по линейному закону от энерговыработки, степени выгорания, а при постоянном уровне мощности реактора - и во времени.
 
Этот вывод имеет практическое значение при выполнении некоторых эксплуатационных расчётов, в чём нам предстоит убедиться в будущем.
 

СМОТРИТЕ ТАКЖЕ: