| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
19.2.4. Характер роста потерь запаса реактивности из-за отравления 135Xe первоначально разотравленного реактора в первый период
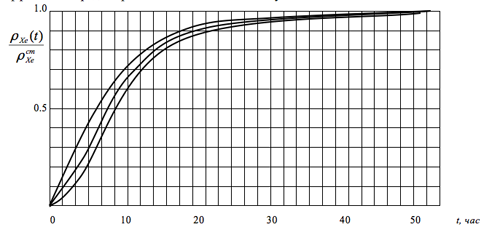
Если реактор запускается после достаточно длительной стоянки и работает на постоянном уровне мощности, то величина потерь реактивности с момента начала работы на мощности от нуля через некоторый отрезок времени в соответствии со всем сказанным ранее должна достигнуть стационарного уровня. Практика должны заинтересовать, по крайней мере, два вопроса: каков характер роста потерь реактивности до достижения уровня стационарного отравления и за какое время работающий на постоянном уровне мощности реактор достигает стационарного отравления? ρXe(t)/ρXeст = 1 + [1/(γI+γXe)] {[λIγI/(λXe+σaXeФо - λI)] - γI} exp[-(λXe + σaXeФо) t] - Формула (19.2.8), если мысленно подставить в неё все нейтронно-физические константы, обретает существенно более простой вид, который подсказывает, что текущие величины отравлений реактора ксеноном нелинейно зависят от уровня мощности реактора (или Фо). Расчёт по этой формуле для различных величин Фо (в том числе и для Фо = ∞)) качественно иллюстрируется графиком, представленным на рис.19.5. Из него следует, что при малых значениях плотности потока тепловых нейтронов (или на малых уровнях мощности реактора) переходный процесс ρXe(t) протекает в несколько более замедленном темпе, чем при больших значениях Фо (на больших уровнях мощности). Предельный случай этих переходных процессов (при Фо → ∞) вырождается в одну экспоненту:
Рис.19.5. Переходные процессы нестационарного выхода первоначально разотравленного реактора на стационарный уровень отравления. Факт не очень существенной зависимости переходных процессов ρXe(t) от плотности потока нейтронов (практически - от мощности реактора) даёт возможность с достаточной для практических целей точностью приближенно оценивать величины текущих значений отравления реактора ксеноном по формуле (19.2.9): СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.