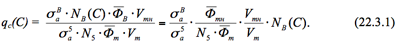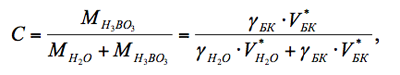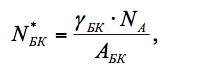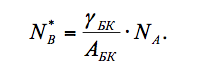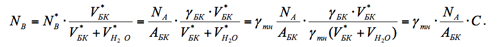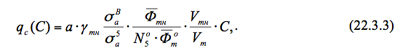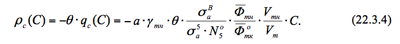Главная >> Лекции по ядерной физике

22.3. Эффективность борной кислоты

Как и подвижные поглотители, эффективность борной кислоты принято оценивать двумя характеристиками, называемыми интегральной и дифференциальной эффективностью борной кислоты.

Интегральной эффективностью борной кислоты при заданной её концентрации в первом контуре С называется величина положительной реактивности, теряемой реактором, при повышении концентрации борной кислоты в его теплоносителе от нуля до этой концентрации С.

Можно выразиться и «наоборот»: интегральная эффективность борной кислоты при текущем значении её концентрации С – есть величина положительной реактивности, высвобождаемой при полном удалении борной кислоты из теплоносителя первого контура РУ.

Интегральная эффективность борной кислоты обозначается символом ρ_с(С) и измеряется в единицах реактивности (а.е.р., проценты, доли β_э и др.).

В соответствии с определением очевидно, что интегральная эффективность борной кислоты при нулевой концентрации борной кислоты равна нулю; по смыслу этого определения можно понять, что интегральная эффективность борной кислоты – величина принципиально отрицательная (: при повышении концентрации борной кислоты запас реактивности реактора только теряется).

Мерой эффекта повышения поглощающей способности активной зоны за счёт введения в неё борной кислоты аналогична по смыслу мерам других подобных эффектов реактивности реактора (отравления, шлакования, воспроизводства и др.) и называется относительным поглощением тепловых нейтронов борной кислотой (или просто бором, поскольку поглощающая способность борной кислоты более чем на 99 % определяется одним компонентом – бором):

Здесь N_B(C), см^-3 – ядерная концентрация бора в теплоносителе;
__    __
Ф_В = Ф_тн, см^-2с^-1 – среднее значение плотности потока тепловых нейтронов, пронизывающего бор в теплоносителе активной зоны реактора;
__
Ф_т, см^-2с^-1 - среднее значение плотности потока тепловых нейтронов, пронизывающего топливо в твэлах активной зоны реактора;
V_тн и V_т, см³ – соответственно объёмы теплоносителя и топливной композиции в активной зоне реактора.

Если предположить, что реактор всю кампанию работает на постоянном уровне мощности, то величина произведения в знаменателе N₅(t)Ф_т(t) = idem = N₅^oФ_т^о, то есть в любой момент кампании определяется произведением этих величин в начале кампании. Ядерная концентрация бора (N_B)  всегда пропорциональна молекулярной концентрации борной кислоты , которая, в свою очередь, всегда пропорциональна массовой концентрации борной кислоты в теплоносителе первого контура (С). Следовательно, первая и последняя из трёх упомянутых величин всегда связаны между собой прямой пропорциональной зависимостью (N_B(C) º C. где a - некоторый постоянный коэффициент пропорциональности).
Небольшой экскурс в химию. Массовая концентрация С, которая используется на АЭС для оценки степени насыщенности теплоносителя борной кислотой, - это доля массы борной кислоты в единичной массе её водного раствора:

где V^*_БК и V_H2O^* - парциальные объёмы борной кислоты и воды в растворе, а γ_БК и γ_H2O - плотности борной кислоты и воды соответственно.
Выражение для массы раствора борной кислоты в воде, стоящее в знаменателе, можно выразить через среднюю величину плотности раствора (обозначим её γ_ТН), умноженную на общий объём раствора  V_тн = V^*_БК + V_H2O^* , то есть:

Молекулярная концентрация борной кислоты в кристаллическом её виде может быть найдена по традиционной формуле через плотность её и число Авогадро:

и эта величина будет равна ядерной концентрации бора в кристаллической борной кислоте (: в каждой молекуле Н₃ВО₃ содержится один атом бора, а, следовательно, и одно ядро бора):

При разбавлении в воде эта концентрация, очевидно, будет уменьшаться пропорционально доле объёма, который занимает борная кислота в растворе:

Итак, ядерная концентрация бора N_B  во всех случаях жизни пропорциональна реальной плотности теплоносителя γ_тн и величине принятой в расчётах массовой концентрации С:

N_B = a·γ_тн·C                                        (22.3.2)
где символом а для краткости обозначена комбинация двух констант (N_A/A_БК).
С учётом этих замечаний, выражение (22.3.1) приобретает вид:

Потери реактивности от введения в теплоноситель в реакторе бора (то есть величина интегральной эффективности борной кислоты) связаны с величиной q_c(C) пропорциональной связью, причём, как и в других эффектах реактивности коэффициентом пропорциональности служит коэффициент использования тепловых нейтронов в реакторе без борной кислоты:

Из (22.3.4) можно заключить, что величина интегральной эффективности борной кислоты изменяется пропорционально текущему значению концентрации её в воде первого контура. Это означает, что в процессе кампании с уменьшением С величина интегральной эффективности борной кислоты уменьшается во времени по линейному закону. На деле имеет место заметное отклонение от линейности, которое объясняется тем, что, во-первых, снижение концентрации Н₃ВО₃ в процессе кампании и выполняется как раз ровно настолько, насколько необходимо для поддержания величины θ, снижающейся за счёт выгорания и шлакования основного топлива. Во-вторых, в процессе кампании изменяется (в сторону уменьшения) величина отношения Ф_В/Ф°_тк, являющегося коэффициентом проигрыша в использовании тепловых нейтронов.

Дифференциальной эффективностью борной кислоты α_с(С) при заданной её концентрации в воде 1 контура С называется изменение реактивности реактора при единичном (на 1 г/кг) её увеличении сверх этой концентрации.

Как следует из определения, дифференциальная эффективность борной кислоты является логическим аналогом дифференциальной эффективности подвижных поглотителей, и называется она так потому, что представляет собой производную интегральной эффективности борной кислоты при рассматриваемой её концентрации С в контуре:

Следовательно, величина интегральной эффективности кислоты при данной её концентрации связана с дифференциальной эффективностью интегральной зависимостью:

Поскольку концентрацию борной кислоты принято измерять в г/кг, наиболее употребительной размерностью дифференциальной эффективности борной кислоты является %/г/кг.
При больших (> 10 г/кг) изменениях концентрации борной кислоты изменения реактивности, обусловленные изменением её концентрации, учитывая нелинейность зависимости ρ_с(С), должны находиться как разница интегральных эффективностей борной кислоты при конечной и начальной её концентрациях:

При относительно небольших изменениях концентрации борной кислоты (< 6 г/кг, что чаще всего и имеет место в эксплуатационной практике) нелинейностью зависимости ρ_с(С) можно пренебречь и находить изменение реактивности вследствие изменения концентрации борной кислоты по формуле:

в которой знак приблизительности равенства указывает на тот факт, что в небольших интервалах изменения концентрации ΔС = С₁ - С₂ зависимость ρ_с(С) можно считать приблизительно линейной, а, следовательно, величину дифференциальной эффективности кислоты α_с – постоянной.

Дифференциальная эффективность борной кислоты  α_с, как и интегральная её эффективность, - величина принципиально отрицательная (: единичное увеличение концентрации кислоты в воде контура всегда приводит к потере оперативного запаса реактивности). Поэтому знак изменений запаса реактивности реактора вследствие изменений концентрации кислоты в теплоносителе при расчёте по формуле (22.3.7) учитывается автоматически: если С₂ > С₁ (то есть имеет место увеличение концентрации кислоты в контуре), то величина Δρ_с получается отрицательной (запас реактивности реактора теряется); если же С₂ < С₁ (концентрация снижается), то величина Δρ_с получается положительной, что свидетельствует о высвобождении запаса реактивности.

Сказанное позволяет оператору РУ легко рассчитывать любые изменения запаса реактивности вследствие изменений концентрации борной кислоты при одном условии: величина дифференциальной эффективности борной кислоты в момент выполнения этих изменений достоверно известна.

СМОТРИТЕ ТАКЖЕ: