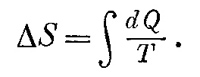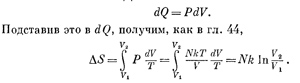Главная >> Фейнмановские лекции по физике >> Том 4 >> Глава 46. Храповик и собачка

Необратимость

Все ли законы физики обратимы? Конечно, нет! Попробуйте-ка, например, из яичницы слепить обратно яйцо! Или пустите фильм в обратную сторону — публика в зале тотчас же начнет смеяться.  Необратимость — самая яркая черта всех событий.
 
Откуда же она появляется? Ведь ее нет в законах Ньютона. Если мы считаем, что любое явление может быть в конечном счете объяснено законами физики, и если также оказывается, что все уравнения обладают фантастическим свойством давать при t→ — t другое решение, то ведь тогда обратимо любое явление. Но как же тогда получается, что в природе, в явлениях большого масштаба, все необратимо? Видимо, значит, есть какие-то законы, какие-то неизвестные нам, но важные уравнения, быть может, в электричестве, а может, в нейтринной физике, для которых уже существенно, куда идет время.
 
Рассмотрим теперь этот вопрос. Один закон такого рода мы уже знаем — он утверждает, что энтропия только растет. Когда одно тело теплое, а другое холодное, тепло переходит от теплого к холодному. Это утверждение нам подошло бы. Но хорошо бы и этот закон понять с точки зрения механики. Нам уже удалось получить при помощи чисто механических соображений все следствия из постулата о том, что тепло не может течь в обратную сторону; это помогло нам понять второй закон. Значит, необратимость из обратимых уравнений получать мы способны. Но использовали ли мы при этом только 8аконы механики? Разберемся в этом глубже.
 
Так как речь зашла об энтропии, то нам придется найти ее микроскопическое описание. Когда мы говорим, что в чем-то (например, в газе) содержится определенное количество энергии, то мы можем обратиться к микроскопической картине этого явления и сказать, что каждый атом имеет определенную энергию. Полная энергия есть сумма энергий атомов. Равным образом, у каждого атома есть своя определенная энтропия. Суммируя, получим полную энтропию. На самом деле здесь все обстоит не так уж гладко, но все же давайте посмотрим, что получится.
 
В виде примера подсчитаем разницу энтропии газа при одной температуре, но в разных объемах. В гл. 44 для изменения энтропии мы получили

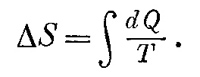В нашем случае энергия газа до и после расширения одна и та же, потому что температура не менялась. Значит, чтобы восполнить работу, проделанную газом, нужно придать ему какое-то количество тепла. Для малых изменений объема

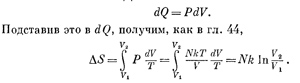Например, при удвоении объема энтропия меняется на Nkln 2.


Рассмотрим теперь другой интересный пример. Пусть имеется цилиндр с перегородкой посредине. По одну ее сторону — неон («черные» молекулы), а по другую — аргон («белые» молекулы). Уберем перегородку и позволим газам перемешаться. Как изменится энтропия? Можно представить себе, что вместо перегородки между газами стоит поршень с отверстиями, в которые проходят белые молекулы и не проходят черные, и другой поршень с обратными свойствами. Сдвигая поршень к основанию цилиндра, легко понять, что для каждого газа задача сводится к только что решенной. Энтропия, таким образом, меняется на Nkln 2; это значит, что энтропия на одну молекулу возрастает на kln 2. Цифра 2 появилась оттого, что вдвое увеличился объем, приходящийся на одну молекулу. Странное обстоятельство! В нем проявилось свойство не самой молекулы, а свободного места вокруг нее. Выходит, что энтропия увеличивается, когда температура и энергия не меняются, а изменилось только распределение молекул!
 
Мы знаем, что стоит убрать перегородку, и газы через некоторое время перемешаются из-за столкновений, колебаний, ударов молекул и т. д. Стоит убрать перегородку, и какая-то белая молекула начнет приближаться к черной, а черная — к белой, они проскочат мимо друг друга и т. д. Постепенно какие-то из белых молекул проникнут случайно в объем, занятый черными, а черные —в область белых. Через какое-то время получится смесь. В общем это необратимый процесс реального мира, он должен привести к росту энтропии.
 
Перед нами простой пример необратимого процесса, полностью состоящего из обратимых событий. Каждый раз, когда происходит столкновение двух молекул, они разлетаются в определенных направлениях. Если запустить киноленту, на которой засняты столкновения, в обратную сторону, то ничего неправильного на экране не появится. Ведь один вид столкновений столь же вероятен, как и другой. Поэтому перемешивание полностью обратимо, и тем не менее оно необратимо. Каждому известно, что, взяв отдельно белое и отдельно черное и перемешав их, мы через несколько минут получим смесь. Подождем еще сколько-то там минут — они не отделятся, смесь останется смесью. Значит, бывает необратимость, основанная на обратимых ситуациях. Но теперь нам ясна и причина. Мы начали с расположения, которое в каком-то смысле упорядочено. В хаосе столкновений оно стало неупорядоченным. Переход от упорядоченного расположения к беспорядочному является источником необратимости.


Конечно, если бы мы сняли на киноленту это движение и пустили бы потом пленку назад, то увидели бы, как постепенно устанавливается порядок. Кто-нибудь мог бы возразить: «Но это — против всех законов физики!» Тогда мы бы прокрутили фильм еще раз и просмотрели бы каждое столкновение. Все они были бы безупречны, каждое подчинялось бы законам физики. Все дело, конечно, в том, что скорости каждой молекулы были бы выдержаны в точности, так что, если проследить их пути вспять, мы возвратимся к начальным условиям. Но такая ситуация крайне маловероятна. Если иметь дело не со специально приготовленным газом, а просто с белыми и черными молекулами, их никогда не удалось бы вернуть назад.

СМОТРИТЕ ТАКЖЕ: