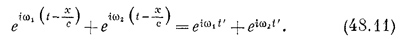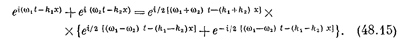| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Локализованный волновой пакет
Следующий вопрос, который мы хотим обсудить,— это интерференция волн как в пространстве, так и во времени. Предположим, что в пространстве распространяются две волны. Вы, конечно, знаете, что распространение волны в пространстве, например звуковой, можно описать с помощью экспоненты exp[i (ωt - kx)]. Такая экспонента удовлетворяет волновому уравнению при условии, что ω2=k2с2, где с — скорость распространения волны. В этом случае экспоненту можно записать в виде exp[ik(z—ct)], что является частным случаем общего решения f(x—ct). Такая экспонента должна описывать волну, распространяющуюся со скоростью ω/k, равной с, и поэтому здесь все в порядке.
При этом, естественно, мы получаем точно такие же модуляции, как и раньше, которые, однако, движутся вместе с волной. Другими словами, если сложить две волны, которые не просто осциллируют, но и перемещаются в пространстве, то получившаяся волна также будет двигаться с той же скоростью.
На самом деле в гл. 31 мы получали и более сложные формулы, однако эта ничуть не хуже, так почему бы нам не взять ее в качестве примера.
Интересно, что, например, для случая распространения рентгеновских лучей в стекле эта фазовая скорость больше скорости света в пустоте [поскольку n, согласно (48.12), меньше единицы], а это несколько неприятно, ведь не думаем же мы, что можно посылать сигналы быстрее скорости света!
где a=Nq2e/2ε0m — постоянная. Во всяком случае, мы хотим сложить такие две волны, у которых для каждой частоты существует определенное волновое число.
Таким образом, снова получается модулированная волна, распространяющаяся со средней частотой и средним волновым числом, однако сила ее меняется в соответствии с выражением, зависящим от разности частот и разности волновых чисел.
Скорость движения модуляций иногда называют групповой скоростью. Если мы возьмем случай относительно малой разности между частотами и соответственно относительно малой разности между волновыми числами, то это выражение переходит в пределе в
Другими словами, чем медленнее модуляции, тем медленнее и биения, и вот что самое удивительное — существует определенная скорость их распространения, которая не равна фазовой скорости волны.
что меньше, чем с! Таким образом, хотя фазы могут бежать быстрее скорости света, модулирующие сигналы движутся медленнее, и в этом состоит разрешение кажущегося парадокса! Разумеется, в простейшем случае ω=kс групповая скорость dω/dk тоже равна с, т. е. когда все фазы движутся с одинаковой скоростью, естественно, и групповая скорость будет той же самой. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.