Главная >> Фейнмановские лекции по физике >> Том 4 >> Глава 51. Волны

Волны в твердом теле

Следующий тип волн, о которых нам следует поговорить,— это волны в твердом теле. Мы уже рассмотрели звуковые волны в жидкости и газе, а между ними и звуковыми волнами в твердом теле имеется непосредственная аналогия. Если резко толкнуть твердое тело, то оно сожмется. Оно сопротивляется сжатию и в нем возникнут волны, аналогичные звуковым. Однако в твердом теле могут быть волны и другого рода, которых не бывает в жидкости. Если мы возбудим колебания твердого тела с помощью бокового давления (это называется сдвигом), то тело стремится вернуться в начальное положение. Именно этим, по определению, твердое тело отличается от жидкого. Если искривить жидкость и подержать ее так немного, чтобы она успокоилась, а затем отпустить, то она останется в том же состоянии, но если мы возьмем твердое тело, похожее на дрожащий кусок желе, надавим на него и отпустим, то оно вернется назад, а в теле возникает волна сдвига, которая распространяется так же, как и волна сжатия. Во всех случаях скорость этих волн меньше скорости продольных волн. В каком-то отношении волны сдвига больше напоминают световые волны, ибо здесь мы тоже имеем дело с поляризацией. У звука нет никакой поляризации, это просто волна сжатия, а световые колебания имеют характерную ориентацию, перпендикулярную к направлению их  распространения.
 
Итак, в твердом теле могут быть волны обоих сортов. Во-первых, там распространяются волны сжатия, аналогичные звуку в воздухе, и, во-вторых, волны сдвига. Если наше твердое тело не кристалл, то волна сдвига может быть поляризована в любом направлении. (Конечно, все твердые тела — кристаллы, но если мы возьмем кусок, состоящий из микрокристаллов всех ориентации,   то   кристаллическая   анизотропия  усредняется.)
 
Есть еще один интересный вопрос, касающийся звуковых волн. Что получится, если длина волны в твердом теле становится все меньше и меньше? До каких пор может это продолжаться? Ясно, что она не может стать меньше расстояния между атомами, ибо если под волной мы понимаем такое явление, когда одна точка идет вниз, а следующая— вверх и т. д., то кратчайшая возможная длина волны при этом, очевидно, равна межатомному расстоянию. Вам известно, что колебания могут быть как продольные, так и поперечные, длинноволновые и коротковолновые.
 
Если мы рассматриваем длины волн, сравнимые с межатомным расстоянием, то скорость уже не будет постоянной; возникает дисперсионный эффект, когда скорость становится зависимой от волнового числа. А высшая гармоника поперечных волн все же должна характеризоваться именно тем, что каждые два соседних атома делают нечто противоположное друг другу.
 
С атомистической точки зрения ситуация здесь напоминает два связанных маятника, о которых мы уже говорили. У них могут быть два вида собственных колебаний: один — когда они качаются вместе, и другой — когда в противоположные стороны. Так что волны в твердом теле можно рассматривать и с иной точки зрения — как колебания связанных гармонических осцилляторов, подобных огромному числу связанных маятнич-ков, причем высшая гармоника получается, когда маятнички колеблются в противоположные стороны, и низшие — при других соотношениях фаз.
 
Эти кратчайшие волны настолько малы, что обычно их невозможно получить технически. Однако они очень интересны, поскольку свойства этих коротких звуковых волн помогают нам объяснить в термодинамической теории твердого тела его тепловые свойства, в частности удельную теплоемкость. Переход к предельно коротким звуковым волнам означает переход к индивидуальному движению атомов; это в конечном счете одно и то же.
 
Очень интересным примером звуковых волн в твердом теле являются волны, идущие по земному шару, как продольные, так и поперечные. Хотя нам и не известно почему, но внутри Земли время от времени происходят землетрясения. Одни породы сдвигаются относительно других, и это движение сходно с очень низким звуком. Из такого источника выходят и путешествуют по всей Земле волны, подобные звуковым, и хотя их длина значительно больше длины обычных звуковых волн, но все же это звуковые волны. Наша Земля не однородна: давление, плотность, сжимаемость и т. д. изменяются с изменением глубины, а поэтому изменяется и скорость. Возникает нечто похожее на показатель преломления, и волны идут не по прямому пути, а по некоторой кривой. Кроме того, картина осложняется тем, что продольные и поперечные волны распространяются с разной скоростью, а поэтому и решения для них будут разными. Если мы в каком-то месте поставим сейсмограф и будем наблюдать, как скачет его самописец после того, как где-то произошло землетрясение, то мы увидим не просто какие-то неправильные прыжки. Мы увидим, как самописец сначала запрыгает, затем успокоится, затем опять запрыгает. Более конкретные детали происходящего зависят от положения сейсмографа. Если он расположен достаточно близко к месту землетрясения, то сначала мы примем продольные волны от возмущения, а уж потом, несколько секунд спустя,— поперечные, ибо они идут медленней. Измеряя разницу времени между их приходами, можно сказать, насколько далеко произошло землетрясение, разумеется, если мы достаточно хорошо знаем скорости и состав внутренних областей.

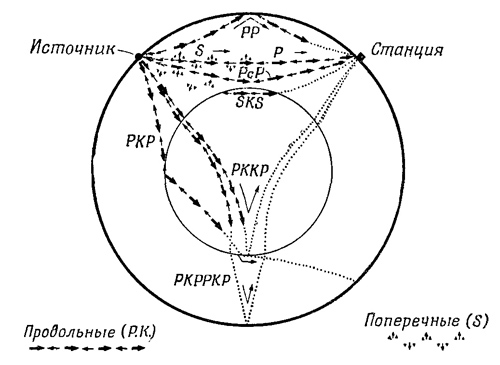На фиг. 51.6 показан пример поведения различных видов волн в Земле. Два сорта волн обозначены различными значками. Если в каком-то месте (назовем его «источник») произошло землетрясение, то поперечные и продольные волны, идущие по прямому пути, придут на станцию в разные моменты времени. Кроме того, возникнут отражения от границ неоднородности, дающие в результате другие пути и времена. Подобные исследования показали, что у Земли есть некое ядро, не проводящее поперечных волн. Однако даже если станция расположена диаметрально противоположно источнику, то поперечные волны все же приходят, но с неправильной фазой. Это получается оттого, что поперечные волны, падающие наклонно на поверхность, разделяющую два вещества, всегда рождают две новые волны: поперечную и продольную. Но внутри ядра Земли поперечные волны не распространяются (по крайней мере в отличие от продольных волн для них этого не обнаружено). Затем на границе ядра оба вида волн возникают вновь и попадают на станцию.
 
Именно по поведению волн, вызванных землетрясениями, было обнаружено, что поперечные волны не могут распространяться в некоторой сфере внутри Земли. Это означает, что центр Земли жидкий в том смысле, что он не проводит поперечных волн. Изучение землетрясений — это единственный источник наших сведений о внутреннем строении Земли. Таким образом, в результате большого числа наблюдений на различных станциях в период многих землетрясений были выяснены все детали; известно все: скорости, кривые и т. д. Мы знаем скорости различных сортов волн на любой глубине. А зная это, мы, следовательно, можем выяснить, каковы собственные гармоники Земли, ибо нам известна скорость распространения звуковых волн: другими словами, известны упругие свойства на любой глубине. Предположим, что мы приплюснули земной эллипсоид и затем отпустили его. Задача определения периода и формы свободных колебаний сводится просто к вопросу о суперпозиции волн, идущих по эллипсоиду. Мы уже выяснили, что при подобном возмущении возникает множество гармоник, начиная от низшей, которая для Земли эллипсоидальна, и вплоть до более высоких и более сложных.

Чилийское землетрясение в мае 1960 г. произвело такой «шум», что его эхо много раз обошло вокруг Земли. Как раз к этому времени были изготовлены новые высокочувствительные сейсмографы, с помощью которых определялись основные гармоники Земли и сравнивались с величинами, вычисленными из теории звука по известным скоростям, найденным из других независимых землетрясений. Результат этого эксперимента показан на фиг. 51.7, где отложена сила сигнала в зависимости от его частоты (фурье-анализ). Заметьте, что одни из принимаемых частот оказывались более сильными, чем другие; наблюдались очень четкие максимумы. Это и есть собственные частоты Земли, поскольку они являются главными частотами ее колебаний.

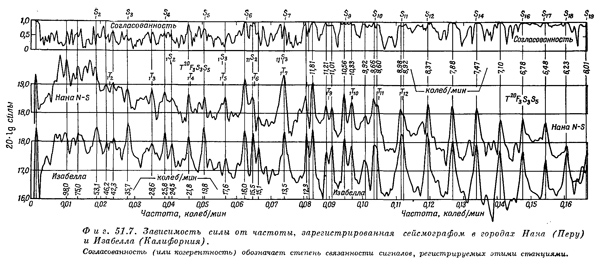
Иными словами, если все движение Земли сводится к суперпозиции множества различных гармоник, то можно надеяться, что запись нерегулярных толчков на любой станции даст одну и ту же суперпозицию многих частот. Если проанализировать это в терминах частот, то мы сможем определить характеристические частоты Земли. Тонкие вертикальные линии на рисунке изображают рассчитанные частоты, и мы видим замечательное согласие, убеждающее нас, что теория звука вполне работает и внутри Земли.

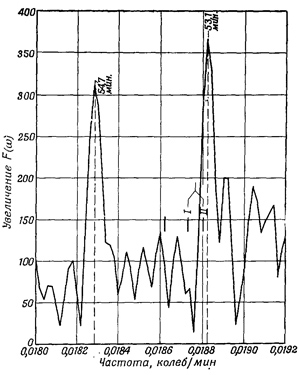Очень интересный факт обнаруживается на фиг. 51.8, где представлены очень точные измерения (с еще большим разрешением) низшей эллипсоидальной гармоники. Заметьте, что здесь не один, а два немного отличающихся максимума: первый — с периодом 54,7 мин и второй — 53,1 мин. Природа этих двух максимумов не была известна, когда они были обнаружены, хотя с тех пор ее могли найти. Существуют по крайней мере два правдоподобных объяснения. Одно из них — это возможная асимметрия в распределении вещества Земли, которая может дать два подобных максимума. Другое, еще более интересное объяснение состоит в следующем. Вообразите волны, идущие от источника вокруг Земли в двух направлениях. Если мы в уравнениях движения учтем эффект вращения Земли, которым обычно пренебрегали при анализе, то скорости этих волн окажутся разными. Движение во вращающейся системе из-за действия кориолисовой силы изменяется, и это может вызвать наблюдаемое расщепление.
 
Коротко о методе получения этих кривых. На сейсмографе мы записываем не зависимость амплитуды от частоты, а перемещение как функцию времени, причем всегда какой-то очень неправильной и причудливой формы.
 
Чтобы найти из нее долю различных синусообразных волн для всех частот, мы уже знаем, что нужно делать. Фокус состоит в умножении полученных данных на синусообразную волну данной частоты и интегрировании, т. е. усреднении; при этом усреднении все другие частоты исчезают.
 
Таким образом, на рисунках фактически показаны графики интегралов от произведения полученных данных на синусообразные волны с различным числом периодов в минуту.

СМОТРИТЕ ТАКЖЕ: