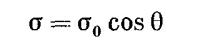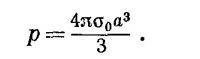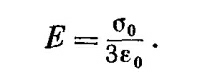| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Дипольный потенциал как градиент
Мы хотели бы теперь отметить любопытное свойство формулы диполя (6.13). Потенциал можно записать также в виде
Действительно, вычислив градиент 1/r, вы получите
и (6.16) совпадет с (6.13).
где Δz означает то же, что и d/2. Беря φ0= q/r, мы получаем для потенциала положительного заряда
Повторяя те же рассуждения с потенциалом отрицательного заряда, можно написать
А общий потенциал—просто сумма (6.17) и (6.18):
При других расположениях диполя смещение положительного заряда можно изобразить вектором Δr+, а уравнение (6.17) представить в виде
где Δr впоследствии надо будет заменить на d/2. Завершая доказательство так, как это было сделано выше, мы приведем уравнение (6.19) к виду
Это то же уравнение, что и (6.16). Надо только заменить qd на р и вставить потерянный по дороге множитель 1/4πε0. Взглянув на это уравнение по-иному, видим, что дипольный потенциал (6.13) можно толковать как
где Фо=1/4πε0r — потенциал единичного точечного заряда.
Когда же нам понадобится потенциал этого распределения, то брать интегралы не нужно. Мы знаем, что потенциал каждого заряженного шара — в точках вне его — совпадает с потенциалом точечного заряда. А два смещенных шара — все равно, что два точечных заряда; значит, искомый потенциал и есть как раз потенциал диполя.
такое же поле, как и диполь с моментом
Можно также показать, что внутри сферы поле постоянно и равно
Если θ — угол с положительной осью z, то электрическое поле внутри сферы направлено по отрицательной оси z. Рассмотренный нами пример отнюдь не досужая выдумка составителя задач; он нам встретится еще в теории диэлектриков. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

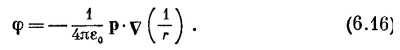
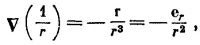
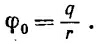
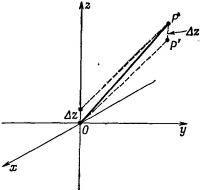 (Множитель 1/4πε0 опустим, а в конце мы его можем снова вставить.) Если заряд +q мы сдвинем на расстояние Δz, то потенциал в точке Р чуть изменится, скажем на Δφ+. На сколько же именно? Как раз на столько, на сколько изменился бы потенциал, если б заряд оставили в покое, а Р сместили на столько же вниз (фиг. 6.5). Иначе говоря,
(Множитель 1/4πε0 опустим, а в конце мы его можем снова вставить.) Если заряд +q мы сдвинем на расстояние Δz, то потенциал в точке Р чуть изменится, скажем на Δφ+. На сколько же именно? Как раз на столько, на сколько изменился бы потенциал, если б заряд оставили в покое, а Р сместили на столько же вниз (фиг. 6.5). Иначе говоря,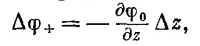
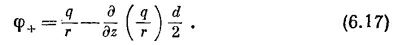
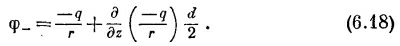
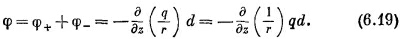
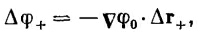
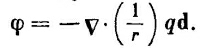

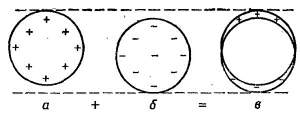 А вот и другой. Пусть имеется сферическая поверхность, на которой поверхностный заряд распределен пропорционально косинусу полярного угла. Интегрировать такое распределение— задача, откровенно говоря, не из приятных. Но как ни странно, на помощь приходит принцип наложения. Представьте себе шар с однородной объемной плотностью положительных зарядов и другой шар с такой же однородной объемной плотностью зарядов, но противоположного знака. Первоначально они вложены друг в друга, образуя нейтральный, т. е. незаряженный шар. Если затем положительный шар чуть сместить по отношению к отрицательному, то нутро незаряженного шара так и останется незаряженным, но на одной стороне возникнет небольшой положительный заряд, а на противоположной — такой же отрицательный (фиг. 6.6). И если относительное смещение двух шаров мало, то эти заряды эквивалентны существованию поверхностного заряда (на сферической поверхности) с плотностью, пропорциональной косинусу полярного угла.
А вот и другой. Пусть имеется сферическая поверхность, на которой поверхностный заряд распределен пропорционально косинусу полярного угла. Интегрировать такое распределение— задача, откровенно говоря, не из приятных. Но как ни странно, на помощь приходит принцип наложения. Представьте себе шар с однородной объемной плотностью положительных зарядов и другой шар с такой же однородной объемной плотностью зарядов, но противоположного знака. Первоначально они вложены друг в друга, образуя нейтральный, т. е. незаряженный шар. Если затем положительный шар чуть сместить по отношению к отрицательному, то нутро незаряженного шара так и останется незаряженным, но на одной стороне возникнет небольшой положительный заряд, а на противоположной — такой же отрицательный (фиг. 6.6). И если относительное смещение двух шаров мало, то эти заряды эквивалентны существованию поверхностного заряда (на сферической поверхности) с плотностью, пропорциональной косинусу полярного угла.