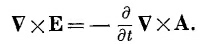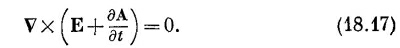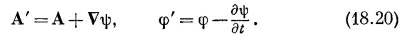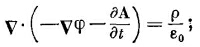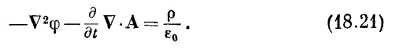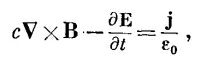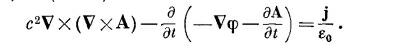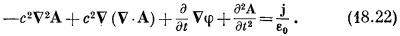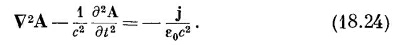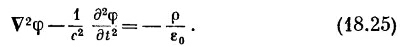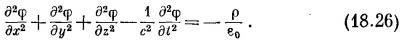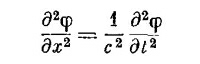| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Решение уравнений Максвелла; потенциалы и волновое уравнение
Теперь стоило бы заняться немного математикой; мы запишем уравнения Максвелла в более простой форме. Вы, пожалуй, сочтете, что мы усложняем их, но если вы наберетесь терпения, то внезапно обнаружите их большую простоту. Хотя вы уже вполне привыкли к каждому из уравнений Максвелла, имеется все же много частей, которые стоит соединить воедино. Вот как раз этим мы и займемся.
то считайте, что уже решили одно из уравнений Максвелла. (Между прочим, заметьте, что оно остается верно для другого вектора А′, если A′=A+ vψ), где ψ — любое скалярное поле, потому что ротор vψ — нуль и В — по-прежнему то же самое. Мы говорили об этом раньше.)
Поскольку мы можем дифференцировать сначала либо по времени, либо по координатам, то можно написать это уравнение также в виде
Мы видим, что E+∂A/∂t — это вектор, ротор которого ранен нулю. Поэтому такой вектор есть градиент чего-то. Когда мы занимались электростатикой, у нас было VxE=0, и мы тогда решили, что Е — само градиент чего-то. Пусть это градиент от –φ (минус для технических удобств). То же самое сделаем и для E+∂A/∂t; мы полагаем
Мы используем то же обозначение φ, так что в электростатическом случае, когда ничто не меняется со временем и ∂A/∂t исчезает, Е будет нашим старым –vφ. Итак, закон Фарадея можно представить в форме
Мы уже решили два из уравнений Максвелла и нашли, что для описания электромагнитных полей Е и В нужны четыре потенциальные функции: скалярный потенциал φ и векторный потенциал А, который, разумеется, представляет три функции.
Тогда ни В, ни Е, полученные из уравнения (18.19), не меняются.
это можно записать еще в виде
Таково первое уравнение, связывающее φ и А с источниками.
а затем выразим В и Е через потенциалы, используя уравнения (18.16) и (18.19):
Первый член можно переписать, используя алгебраическое тождество v x (vxA) = V (V·A) – v2A; мы получаем
Не очень-то оно простое!
Когда мы поступаем так, то второе и третье слагаемые в уравнении (18.22) погашаются, и оно становится много проще:
И наше уравнение (18.21) для φ принимает такую же форму:
Какие красивые уравнения! Они великолепны прежде всего потому, что хорошо разделились — с плотностью заряда стоит φ, а с током стоит А. Далее, хотя левая сторона выглядит немного нелепо — лапласиан вместе с (∂/∂t)2, когда мы раскроем ее, то обнаружим
Это уравнение имеет приятную симметрию по х, у, z, t; здесь (–1/с2) нужно, конечно, потому, что время и координаты различаются; у них разные единицы.
и видели, что оно описывает распространение волн в x-направлении со скоростью с. Уравнение (18.26) это соответствующее волновое уравнение для трех измерений. Поэтому в области, где больше нет зарядов и токов, решение этих уравнений не означает, что φ и А — нули. (Хотя на самом деле нулевое решение есть одно из возможных решений.) Имеются решения, представляющие некоторую совокупность φ и А, которые меняются со временем, но всегда движутся со скоростью с. Поля передвигаются вперед через свободное пространство, как в нашем примере в начале главы. СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.