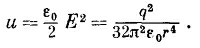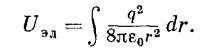Главная >> Фейнмановские лекции по физике >> Том 6 >> Глава 28. Электромагнитная масса

Энергия поля точечного заряда

Синтез теории относительности и уравнений Максвелла в основном завершает наше изучение теории электромагнетизма. Разумеется, по дороге мы перескочили через некоторые детали и оставили незатронутой довольно большую область, к которой, однако, мы еще вернемся в будущем, когда займемся взаимодействием электромагнитного поля с веществом. И все же, если еще задержаться на минуту и посмотреть на фасад этого удивительного сооружения, имевшего столь громадный успех в объяснении столь многих явлений, то можно обнаружить,что оно вот-вот завалится и рассыплется на куски. Если вы поглубже вгрызетесь почти в любую из наших физических теорий, то обнаружите, что в конце концов попадаете в какую-нибудь неприятную историю. Сейчас нам предстоит обсудить серьезную трудность — несостоятельность классической электромагнитной теории. Может показаться, что это нарушение, естественно, связано с падением всей классической теории под ударами квантовомеханических эффектов. Возьмите классическую механику. Математически это вполне самосогласованная теория, хотя она и отвергается опытом. Однако самое интересное, что классическая теория электромагнетизма неудовлетворительна сама по себе. В ней до сих пор есть трудности, которые связаны с самими идеями теории Максвелла и которые не имеют непосредственного отношения к квантовой механике. Вы можете подумать: «А зачем нам заранее беспокоиться об этих трудностях. Ведь квантовая механика все равно изменит законы электродинамики. Не лучше ли подождать   и   посмотреть,   во что превратятся эти трудности после изменений?» Однако трудности остаются и после соединения электродинамики с квантовой механикой, так что рассмотрение их сейчас не будет напрасной тратой времени; вдобавок они очень важны с исторической точки зрения. Кроме того, если вы в силах столь глубоко проникнуть в теорию, чтобы увидеть в ней все, не исключая и трудностей, то это дает вам известное чувство завершенности.
 
Трудность, о которой я собираюсь говорить, связана с приложением понятий электромагнитного импульса и энергии к электрону или другой заряженной частице. Понятия простых заряженных частиц и электромагнитного поля как-то не согласуются друг с другом. Описание этой трудности мы начнем с некоторых примеров вычисления энергии и импульса. Найдем сначала энергию заряженной частицы. Представьте, что мы взяли простейшую модель электрона, когда весь его заряд q равномерно распределен по поверхности сферы радиусом а. В специальном случае точечного заряда мы можем положить его равным нулю. Теперь вычислим энергию электромагнитного поля. Если заряд неподвижен, то никакого магнитного поля вокруг нет, и энергия в единице объема будет пропорциональна квадрату напряженности электрического поля. Величина же напряженности электрического поля равна q/4πε₀r², поэтому плотность энергии

Чтобы получить полную энергию, нужно эту плотность проинтегрировать по всему пространству. Используя элемент объема 4πr²dr, найдем полную энергию, которую мы обозначим через U_эл:

Это выражение интегрируется очень просто.  Нижний предел интегрирования равен а, а верхний — бесконечности, поэтому

Если вместо q подставить заряд электрона q_e и обозначить символом е² комбинацию q_e²/4πε₀, то получим

Все идет хорошо до тех пор, пока мы не переходим к точечному заряду, т. е. пока мы не положим а=0. Но как только мы переходим к точечному заряду, начинаются все наши беды. И все потому, что энергия поля изменяется обратно пропорционально четвертой степени расстояния, интеграл по объему становится расходящимся, а количество  энергии, окружающей   точечный заряд, оказывается бесконечным.
 
Но чем, собственно, плоха бесконечная энергия? Есть ли какая-то реальная трудность в том, что энергия никуда не может уйти от заряда и обречена навсегда оставаться около него? Досадно, конечно, что величина оказалась бесконечной, но главный вопрос в том — есть ли здесь какой-нибудь наблюдаемый физический эффект? Чтобы ответить на него, нужно обратиться не к энергии, а к чему-то другому. Нас может, скажем, заинтересовать, как изменяется энергия, когда заряд движется. Если при этом окажется бесконечным изменение, то дело совсем плохо.

СМОТРИТЕ ТАКЖЕ: