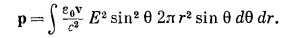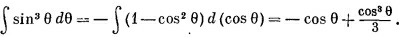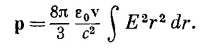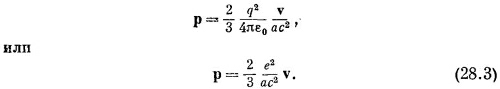| Обучение и материалы |
|---|
| Физический справочник |
| Формулы по физике |
| Шпаргалки по физике |
| Энциклопедия |
| Репетиторы по физике |
| Работа для физиков |
| Быстрый устный счет |
| Виртуальные лабораторные |
| Опыты по физике |
| ЕГЭ онлайн |
| Онлайн тестирование |
| Ученые физики |
| Необъяснимые явления |
| Ваша реклама на сайте |
| Разное |
| Контакты |
| Спецкурс |
|---|
| Фейнмановские лекции |
|
В мире больших скоростей |
Введение в теорию относительности |
|
Лекции по биофизике |
| Лекции по ядерной физике |
| Ускорение времени... |
| Лазеры |
| Нанотехнологии |
| Книги |
| полезное |
|---|
| Смешные анекдоты о физике
Готовые шпоры по физике Физика в жизни Ученые и деньги Нобелевские лауреаты Фото Видео Карта сайта |
| На заметку |
|---|
| Если вам понравился сайт, предлагаем разместить нашу кнопку |
| Дополнительно |
|---|
|
Компьютерные программы по физике 
Физика и юмор 
Онлайн тестирование по физике 
|
Импульс поля движущегося заряда
Она обязательно направлена по линии движения, как это видно из рисунка, и по величине равна
Поскольку Е не зависит от угла θ (для v«c) , то по углу можно немедленно проинтегрировать:
Интегрирование по θ ведется в пределах от 0 до π, так что этот интеграл дает просто множитель 4/3, т. е.
А такой интеграл (для v«c) мы только что вычисляли, чтобы найти энергию; он равен q2/16π2ε02а, так что
Импульс поля, т. е. электромагнитный импульс, оказался пропорциональным v. В частности, тоже самое выражение получилось бы для частицы с массой, равной коэффициенту пропорциональности при v. Вот почему этот коэффициент пропорциональности мы можем назвать электромагнитной массой тэм, т. е. положить
СМОТРИТЕ ТАКЖЕ:Социальные комментарии Cackle |
© All-Физика, 2009-2026
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.
При использовании материалов сайта ссылка на www.all-fizika.com обязательна.

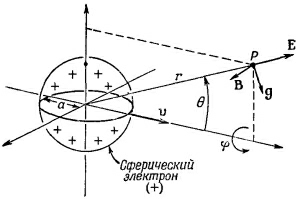 Возьмем равномерно движущийся электрон и предположим на минуту, что скорость его мала по сравнению со скоростью света. С таким движущимся электроном всегда связан какой-то импульс — даже если у электрона до того, как он был заряжен, не было никакой массы — это импульс электромагнитного поля. Мы покажем, что для малых скоростей он пропорционален скорости v и совпадает с ней по направлению. В точке Р, находящейся на расстоянии r от центра заряда и под углом θ к линии его движения (фиг. 28.1), электрическое поле радиально, а магнитное, как мы видели, равно vXE/c2. Плотность же импульса, в соответствии с формулой (27.21), будет
Возьмем равномерно движущийся электрон и предположим на минуту, что скорость его мала по сравнению со скоростью света. С таким движущимся электроном всегда связан какой-то импульс — даже если у электрона до того, как он был заряжен, не было никакой массы — это импульс электромагнитного поля. Мы покажем, что для малых скоростей он пропорционален скорости v и совпадает с ней по направлению. В точке Р, находящейся на расстоянии r от центра заряда и под углом θ к линии его движения (фиг. 28.1), электрическое поле радиально, а магнитное, как мы видели, равно vXE/c2. Плотность же импульса, в соответствии с формулой (27.21), будет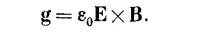
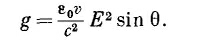
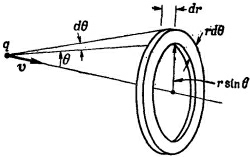 Поле симметрично относительно линии движения заряда, поэтому поперечные компоненты дадут в сумме нуль, и полученный в результате импульс будет параллелен скорости v. Величину составляющей вектора g в этом направлении, равную g sin θ, нужно проинтегрировать по всему пространству. В качестве элемента объема возьмем кольцо, плоскость которого перпендикулярна v (фиг. 28.2). Объем его равен 2πr2sin θ dθ dr. Полный импульс будет при этом
Поле симметрично относительно линии движения заряда, поэтому поперечные компоненты дадут в сумме нуль, и полученный в результате импульс будет параллелен скорости v. Величину составляющей вектора g в этом направлении, равную g sin θ, нужно проинтегрировать по всему пространству. В качестве элемента объема возьмем кольцо, плоскость которого перпендикулярна v (фиг. 28.2). Объем его равен 2πr2sin θ dθ dr. Полный импульс будет при этом