Главная >> Фейнмановские лекции по физике >> Том 6 >> Глава 28. Электромагнитная масса Попытки изменения теории Максвелла
Теперь мне бы хотелось обсудить, как можно изменить электродинамику Максвелла, но изменить так, чтобы сохранить понятие простого точечного заряда. В этом направлении было сделано немало попыток, а некоторые теории сумели даже так представить дело, что вся масса электрона оказалась полностью электромагнитной. Однако ни одной из этих теорий не суждено было выжить. И все же интересно обсудить некоторые из предложенных возможностей хотя бы для того, чтобы оценить борьбу человеческого разума.
Наша теория электромагнетизма началась с разговоров о взаимодействии одного заряда с другим. Затем мы построили теорию этих взаимодействующих зарядов и закончили наше изучение теорией поля. Мы настолько уверовали в нее, что пытались с ее помощью определить, как одна часть электрона действует на другую. Все трудности, возможно, происходят из-за того, что электрон не действует сам на себя; экстраполяция закона взаимодействия между отдельными электронами на взаимодействие электрона самого с собой, возможно, ничем не оправдана. Поэтому некоторые из предложенных теорий совсем исключают возможность самодействия электрона. Из-за этого в них уже не возникает бесконечностей. И никакой электромагнитной массы при этом у частиц нет, а ее масса снова полностью механическая. Однако в такой теории возникают новые трудности.
Нужно сразу же вам сказать, что такие теории требуют изменения и понятий электромагнитного поля. Как вы помните, мы говорили, что сила, действующая на частицу в любой точке, определяется просто двумя величинами: Е и В. Если мы отказываемся от идеи самодействия, то это утверждение становится уже несправедливым, ибо силы, действующие на электрон в некотором месте, больше не определяются полными Е и В, а только теми их частями, которые создаются другими зарядами. Так что мы всегда должны помнить о том, какие поля Е и В создает тот заряд, для которого вычисляется действующая сила, а какие — все остальные заряды. Это делает теорию гораздо более запутанной, хотя и позволяет избежать трудностей с бесконечностями.
Итак, если нам очень хочется, мы можем выбросить весь набор сил в уравнении (28.9), приговаривая при этом, что такое явление, как действие электрона на себя, отсутствует. Но вместе с водой мы выплескиваем и ребенка! Ведь второе-то слагаемое в (28.9), слагаемое с х, совершенно необходимо. Эта сила приводит к вполне определенному эффекту. Если вы ее выбросите — беды не миновать. Когда вы разгоняете заряд, он излучает электромагнитные волны, т. е. теряет энергию. Поэтому ускорение заряда требует большей силы, чем ускорение нейтрального объекта той же массы; в противном случае энергия не будет сохраняться. Скорость, с которой мы затрачиваем работу на ускорение заряда, должна быть равна скорости потери энергии на излучение. Мы уже говорили об этом эффекте; он был назван радиационным сопротивлением. Снова перед нами вопрос: откуда берутся те дополнительные силы, на преодоление которых затрачивается эта работа? Когда излучает большая антенна, то эти силы возникают под влиянием токов одной ее части на токи в другой. Но у отдельного ускоряющегося электрона, излучающего в пустое пространство, возможен только один источник таких сил — действие одной части электрона на другую.
В гл. 32 (вып. 3) мы обнаружили, что осциллирующий заряд излучает энергию со скоростью
 |
Давайте посмотрим, какая мощность необходима для преодоления силы самодействия (28.9). Мощность, как известно, равна силе, умноженной на скорость, т. е. Fx:
Первый член пропорционален dx2/dt и поэтому соответствует скорости изменения кинетической энергии 1/2mv2, связанной с электромагнитной массой. А второй соответствует излучению мощности (28.10). Однако он отличается от (28.10). Разница состоит в том, что (28.11) справедливо в общем случае, тогда как (28.10) верно только для осциллирующего заряда. Мы можем доказать, что эти два выражения для периодического движения заряда эквивалентны. Перепишем для этого второй член выражения (28.11) в виде
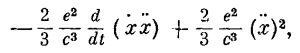 |
что будет просто алгебраическим преобразованием. Если движение электрона периодическое, то величина хх периодически возвращается к одному и тому же значению. Так что если мы возьмем среднее значение ее производной по времени, то получим нуль. Однако второй член всегда положителен (как квадрат величины), так что его производная тоже положительна. Соответствующая ему мощность как раз равна выражению (28.10).
Итак, слагаемое с x в выражении для силы самодействия необходимо для сохранения энергии излучающей системы и не может быть выброшено. Это было одним из триумфов теории Лоренца, доказавшего возникновение такого слагаемого в результате воздействия электрона самого на себя. Мы вынуждены поверить в идею самодействия и необходимость слагаемого с х. Проблема в том, как сохранить его, избавившись при этом от первого слагаемого в выражении (28.9), которое портит все дело. Этого мы не знаем. Как видите, классическая теория электрона сама себя завела в тупик.
Были предприняты и другие попытки выправить положение. Один путь был предложен Борном и Инфельдом. Состоит он в очень сложном изменении уравнений Максвелла, так что они перестают быть линейными. При этом можно сделать так, чтобы энергия и импульс оказались конечными. Но предложенные ими законы предсказывают явления, которые никогда не наблюдались. Их теория страдает еще и другим недостатком, к которому мы придем позднее и который присущ всем попыткам избежать описанную трудность.
Следующая интересная возможность была предложена Дираком. Он рассуждал так: давайте допустим, что действие электрона на себя описывается не первым слагаемым выражения (28.9), а вторым. И тогда ему пришла заманчивая идея избавиться от первого слагаемого, сохранив при этом второе. Смотрите — сказал он,— когда мы брали только запаздывающие решения уравнений Максвелла, это условие выступало как дополнительное предположение; если бы вместо запаздывающих мы взяли опережающие волны, то ответ получился бы несколько другим. Выражение для силы самодействия приобрело бы вид
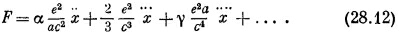 |
Это выражение в точности такое же, как и (28.9), за исключением знака перед вторым и некоторыми высшими членами ряда. [Замена запаздывающих волн опережающими означает просто смену знака запаздывания, что, как нетрудно видеть, эквивалентно изменению знака t. В выражении (28.9) это приводит только к изменению знака всех нечетных производных.] Итак, Дирак предложил: давайте примем новое правило, что электрон действует на себя полуразностью создаваемых им запаздывающих и опережающих полей. Полуразность выражений (28.9) и (28.12) дает
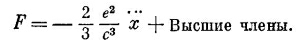 |
Во всех высших членах радиус а входит в числитель в положительной степени. Поэтому, когда мы переходим к пределу точечного заряда, остается только один член — как раз тот, который нам нужен. Таким путем Дирак сохранил радиационное сопротивление и избавился от силы инерции. Электромагнитная масса исчезла, классическая теория спасена, но благополучие это достигнуто ценой насилия над самодействием электрона.
Произвол дополнительных предположений Дирака был устранен, по крайней мере до некоторой степени, Уилером и Фейнманом, которые предложили еще более странную теорию. Они предположили, что точечный заряд взаимодействует только с другими зарядами, но взаимодействие идет наполовину через запаздывающие, наполовину через опережающие волны. Самое удивительное, как оказалось, что в большинстве случаев вы не видите эффекта опережающих волн, но они дают как раз нужную силу радиационного сопротивления. Однако радиационное сопротивление возникает не как самодействие электрона, а в результате следующего интересного эффекта. Когда электрон ускоряется в момент t, то он влияет на все другие заряды в мире в поздний момент t′ = t+r/c (где r — расстояние до других зарядов) из-за запаздывающих волн. Но затем эти другие заряды действуют снова на первоначальный электрон с помощью опережающих волн, которые приходят к нему в момент t″, равный t′ минус r/с, что как раз равно t. (Они, конечно, воздействуют и с помощью запаздывающих волн, но это просто соответствует обычным «отраженным» волнам.) Комбинация опережающих и запаздывающих волн означает, что в тот момент, когда электрон ускоряется, осциллирующий заряд испытывает воздействие силы со стороны всех зарядов, которые «приготовились» поглотить излученные им волны. Вот в какой петле запутались физики, пытаясь спасти теорию электрона!
Я расскажу вам еще об одной теории, чтобы показать, до каких вещей додумываются люди, когда они увлечены. Это несколько другая модификация законов электродинамики, которую предложил Бопп.
Вы понимаете, что, решившись изменить уравнения электромагнетизма, можно делать это в любом месте. Вы можете изменить закон сил, действующих на электрон, или можете изменить уравнения Максвелла (как это будет сделано в теории, которую я собираюсь описать) или еще что-нибудь. Одна из возможностей — изменить формулы, определяющие потенциал через заряды и токи. Возьмем формулу, которая выражает потенциалы в некоторой точке через плотности токов (или зарядов) в любой другой точке в ранний момент времени. С помощью четырехвекторных обозначений для потенциалов мы можем записать ее в виде
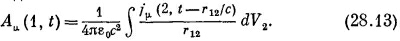 |
Удивительно простая идея Боппа заключается в следующем. Может быть, все зло происходит от множителя 1/r под интегралом. Предположим с самого начала, что потенциал в одной точке зависит от плотности зарядов в любой точке как некоторая функция расстояния между точками, скажем как f (r12). Тогда полный потенциал в точке 1 будет определяться интегралом по всему пространству от произведения jμ на эту функцию
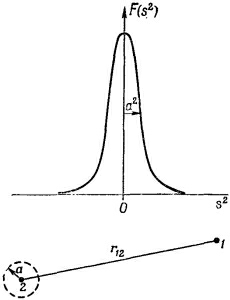
Вот и все. Никаких дифференциальных уравнений, ничего больше. Есть только еще одно условие. Мы должны потребовать, чтобы результат был релятивистски инвариантным. Так что в качестве «расстояния» мы должны взять инвариантное «расстояние» между двумя точками в пространстве-времени. Квадрат этого расстояния (с точностью до знака, который несуществен) равен
Так что для релятивистской инвариантности теории функция должна зависеть от s12 или, что то же самое, от s212. Таким образом, в теории Боппа
 (Интеграл, разумеется, должен браться по четырехмерному объему dt2dx2dy2dz2.) (Интеграл, разумеется, должен браться по четырехмерному объему dt2dx2dy2dz2.)
Теперь остается только выбрать подходящую функцию F. Относительно нее мы предполагаем только одно, что она повсюду мала, за исключением области аргумента вблизи нуля, т. е. что график F ведет себя подобно кривой, изображенной на фиг. 28.4. Это узкий пик в окрестности s2=0, шириной которого грубо можно считать величину а2. Если вычисляется потенциал в точке 1, то приближенно можно утверждать, что заметный вклад дают только те точки 2, для которых s212=c2(t2–t1)2–r212 отличается от нуля на ±а2. Это можно выразить, сказав, что F важно только для
Если понадобится, можно проделать все математически более строго, но идея вам уже ясна.
Предположим теперь, что а очень мало по сравнению с размерами обычных объектов типа электромоторов, генераторов и тому подобное, поэтому для обычных задач r12»а. Тогда выражение (28.16) говорит, что в интеграл (28.15) дают вклад только те токи, для которых t1–t2 очень мало:
Но поскольку а2/r212«1, то квадратный корень приближенно равен 1±а2/2r212, так что
В чем здесь суть? Полученный результат говорит, что для Aμ в момент t1 важны только те времена t2, которые отличаются от него на запаздывание r12/с с пренебрежимо малой поправкой, ибо r12»а. Другими словами, теория Бонна переходит в теорию Максвелла при удалении от зарядов в том смысле, что она приводит к эффекту запаздывания.
Мы можем приближенно увидеть, к чему нас приведет интеграл (28.15). Если, зафиксировав r12, провести интегрирование по t2 в пределах от –∞ до +∞,то s212 тоже будет изменяться от –∞ до +∞. Но основной вклад даст участок по t2 шириной Δtz=2·а2/2r12с с центром в момент t1–r12/с. Пусть функция F (s2) при s2=0 принимает значение К, тогда интегрирование по t2 дает приблизительно KjμΔt2, или
Разумеется, величину jμ следует взять в момент t2=t1–r12/с, так что (28.15) принимает вид
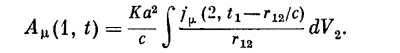 |
Если выбрать K=q2c/4πε0a2, то мы придем прямо к запаздывающему решению уравнений Максвелла для потенциалов, причем автоматически возникает зависимость 1/r! И все это получилось из простого предположения, что потенциал в одной точке пространства-времени зависит от плотности токов во всех других точках пространства-времени с весовым множителем, в качестве которого взята некая функция четырехмерного расстояния между двумя точками. Эта теория тоже дает конечную электромагнитную массу электрона, а соотношение между энергией и массой как раз такое, какое требуется в теории относительности. Ничего другого не могло и быть, ибо теория релятивистски инвариантна с самого начала.
Однако и этой теории и всем другим описанным нами теориям можно предъявить тяжкое обвинение. Все известные нам частицы подчиняются законам квантовой механики, поэтому необходима квантовомеханическая форма электродинамики. Свет ведет себя подобно фотонам. Это уже не 100-процентная теория Максвелла. Следовательно, электродинамика должна быть изменена. Мы уже говорили, что упорное старание исправить классическую теорию может оказаться напрасной тратой времени, ибо в квантовой электродинамике трудности могут исчезнуть или будут разрешены другим образом. Однако и в квантовой электродинамике трудности не исчезают. В этом кроется одна из причин, почему люди потратили столько времени, пытаясь преодолеть классические трудности и надеясь, что если они смогут преодолеть их, то после квантового обобщения уравнений Максвелла все будет в порядке. Однако и после такого обобщения трудности не исчезают.
Квантовые эффекты, правда, приводят к некоторым изменениям. Изменяется формула для масс, появляется постоянная Планка h, но ответ по-прежнему выходит бесконечным, если вы не обрезаете как-то интегрирование, подобно тому как мы обрезали интеграл при r=а в классической теории. Ответ при этом зависит от характера обрезания. К сожалению, я не могу вам показать, что трудности в основном те же самые, ибо вы еще слишком мало знаете о квантовой механике, а о квантовой электродинамике — и того меньше. Поэтому вам придется поверить мне на слово, что и квантовая электродинамика Максвелла приводит к бесконечной массе точечного электрона.
Оказывается, однако, что до сих пор никому не удалось даже приблизиться к самосогласованному квантовому обобщению на основе любой из модифицированных теорий. Идее Борна и Инфельда никогда не суждено было стать квантовой теорией. Не привели к удовлетворительной квантовой теории опережающие и запаздывающие волны Дирака и Уилера — Фейнмана. Не привела к удовлетворительной квантовой теории и идея Боппа. Так что и до сего дня нам не известно решение этой проблемы. Мы не знаем, как с учетом квантовой механики построить самосогласованную теорию, которая не давала бы бесконечной собственной энергии электрона или какого-то другого точечного заряда. И в то же время нет удовлетворительной теории, которая описывала бы неточечный заряд. Так эта проблема и осталась нерешенной.
Если вы вздумаете попытать счастья и построить теорию, полностью удалив действие электрона на себя, так чтобы электромагнитная масса не имела смысла, а затем будете делать из нее квантовую теорию, то могу вас заверить — трудностей вы не избежите. Экспериментально доказано существование электромагнитной инерции и тот факт, что часть массы заряженных частиц — электромагнитная по своему происхождению.
В старых книгах часто утверждалось, что поскольку природа не подарила нам двух одинаковых частиц, из которых одна нейтральная, а другая заряженная, то мы никогда не сможем сказать, какая доля массы является электромагнитной, а какая механической. Однако оказалось, что природа все же была достаточна щедра и подарила нам именно два таких объекта, так что, сравнивая наблюдаемую массу заряженной частицы с массой нейтральной, мы можем сказать, существует ли электромагнитная масса. Возьмем, например, нейтрон и протон. Они взаимодействуют с огромней силой — ядерной силой, детали происхождения которой нам неизвестны. Однако, как мы уже говорили, ядерные силы обладают одним замечательным свойством. По отношению к этим силам нейтрон и протон в точности одинаковы. Насколько мы сейчас можем судить, ядерные силы между двумя нейтронами, нейтроном и протоном и двумя протонами совершенно одинаковы. Отличаются эти частицы только сравнительно слабыми электромагнитными силами; по отношению к ним протон и нейтрон отличаются, как день и ночь. Вот это нам как раз и нужно. Итак, мы имеем две частицы, одинаковые с точки зрения сильных взаимодействий и различных с точки зрения электрических. И они имеют небольшую разницу в массах. Разница масс между протоном и нейтроном, выраженная в единицах энергии покоя тс2, составляет 1,3 Мэв, что соответствует 2,6 электронным массам. Классическая теория предсказывает для радиуса протона величину между 1/3 и 1/2 радиуса электрона, или около 10-13 см. Конечно, на самом деле следует пользоваться квантовой теорией, но по какой-то странной случайности все константы, 2π, h и т. д., комбинируются так, что приблизительно дают тот же самый результат, что и классическая теория. Одна беда: знак оказывается неверным! Нейтрон на самом деле тяжелее протона.
Природа дала нам еще несколько других пар и троек частиц, которые, за исключением электрического заряда, во всех остальных отношениях оказываются в точности одинаковыми. Они взаимодействуют с протонами и нейтронами посредством так называемого «сильного» взаимодействия. В таких взаимодействиях все частицы данного сорта, скажем π-мезон, ведут себя во всех отношениях как одна и та же частица, за исключением их электрического заряда.
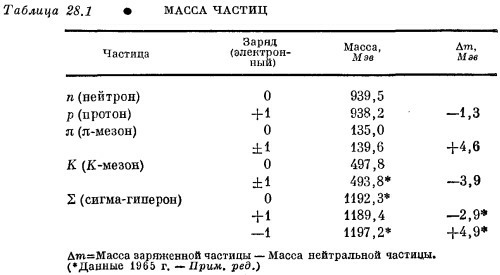
В табл. 28.1 мы приводим список таких частиц вместе с их массами. Заряженные π-мезоны имеют массу 139,6 Мэв, а нейтральный π0-мезон на 4,6 Мэв легче. Эту разность масс мы считаем электромагнитной. Она соответствовала бы частице с радиусом от 3 до 4·10–14 см. Вы видите из таблицы, что разницы масс других частиц того же масштаба.
 |
Однако размеры этих частиц можно определить и другими методами, например по кажущемуся диаметру при высокоэнергетических соударениях. Таким образом, электромагнитная масса, по-видимому, находится в согласии с электромагнитной теорией, если мы обрезаем интеграл от энергии поля на радиусе, полученном этими другими методами. Вот почему мы верим, что разница все же обусловлена электромагнитной массой.
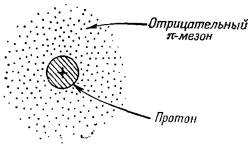 Вас, конечно, беспокоят разные знаки разности масс в таблице. Нетрудно понять, почему заряженная частица должна быть тяжелее нейтральной. Но что можно сказать о таких парах, как нейтрон и протон, где наблюдаемая разность масс оказывается совсем другой? Эти частицы оказываются довольно сложными, и вычисление их электромагнитной массы более хитро. Например, хотя нейтрон в целом нейтрален, у него все же есть внутреннее распределение заряда и равен нулю только суммарный заряд. Мы думаем, что нейтрон, по крайней мере в некоторые моменты времени, выглядит как протон, окруженный «облаком» отрицательного π-мезона (фиг. 28.5). И несмотря на то, что нейтрон «нейтрален», т. е. полный его заряд равен нулю, у него все же есть какая-то электромагнитная энергия (например, у него есть магнитный момент), так что без детальной теории внутренней структуры судить о знаке электромагнитной разности масс нелегко. Вас, конечно, беспокоят разные знаки разности масс в таблице. Нетрудно понять, почему заряженная частица должна быть тяжелее нейтральной. Но что можно сказать о таких парах, как нейтрон и протон, где наблюдаемая разность масс оказывается совсем другой? Эти частицы оказываются довольно сложными, и вычисление их электромагнитной массы более хитро. Например, хотя нейтрон в целом нейтрален, у него все же есть внутреннее распределение заряда и равен нулю только суммарный заряд. Мы думаем, что нейтрон, по крайней мере в некоторые моменты времени, выглядит как протон, окруженный «облаком» отрицательного π-мезона (фиг. 28.5). И несмотря на то, что нейтрон «нейтрален», т. е. полный его заряд равен нулю, у него все же есть какая-то электромагнитная энергия (например, у него есть магнитный момент), так что без детальной теории внутренней структуры судить о знаке электромагнитной разности масс нелегко.
Мне хотелось бы подчеркнуть лишь следующие особенности:
1.Электромагнитная теория предсказывает существование электромагнитной массы, но она тут же терпит фиаско, ибо оказывается несамосогласованной. Это в равной мере относится и к квантовым модификациям.
2.Существует экспериментальное подтверждение электромагнитной массы.
3.Все разности масс по порядку величины такие же, как и масса электрона.
Итак, мы снова возвращаемся к первоначальной идее Лоренца, что масса электрона вполне может быть целиком электромагнитной, т. е. все его 0,511 Мэв обусловлены электродинамикой. Так это или нет? У нас нет теории и по сей день, поэтому мы ничего не можем сказать с уверенностью.
Мне хочется упомянуть еще об одном досадном обстоятельстве. В природе существует еще одна частица, называемая μ-мезоном, или мюоном, которая, насколько нам известно сегодня, решительно ничем не отличается от электрона, за исключением своей массы (равной 206,77 электронных масс). Она во всем ведет себя так же, как электрон: взаимодействует с нейтрино и электромагнитным полем, но на нее не действуют ядерные силы. С ней не происходит ничего такого, чего не происходит с электронами, по крайней мере ничего такого, чего нельзя было бы объяснить, как простое следствие большей массы. Поэтому, если в конце концов кому-то и удается объяснить массу электрона, для него остается загадкой, откуда же берет свою массу μ-мезон. Почему? Да потому, что все, что делает электрон, может делать и μ-мезон, так что массы их должны получиться одинаковыми. Есть люди, которые непоколебимо верят, что μ-мезон и электрон — это одна и та же частица, что в окончательной будущей теории масс формула, из которой они должны определяться, будет представлять собой квадратное уравнение с двумя корнями, один из которых даст массу μ-мезона, а другой — электрона. Есть и такие, которые полагают, что это будет трансцендентное уравнение с бесконечным числом корней; они занимаются гаданием, какими должны быть массы других частиц этого ряда и почему они не открыты до сих пор.
СМОТРИТЕ ТАКЖЕ:
Социальные комментарии Cackle
|





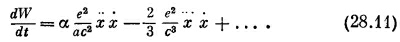
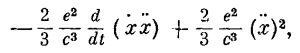
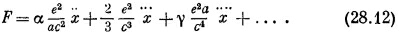
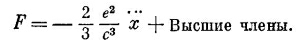
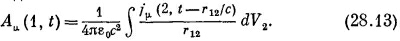
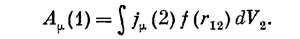
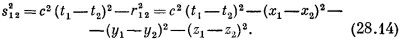
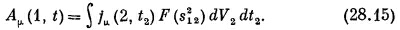
 (Интеграл, разумеется, должен браться по четырехмерному объему dt2dx2dy2dz2.)
(Интеграл, разумеется, должен браться по четырехмерному объему dt2dx2dy2dz2.)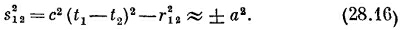
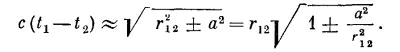
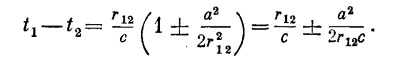
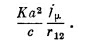
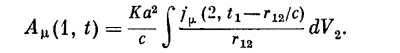

 Вас, конечно, беспокоят разные знаки разности масс в таблице. Нетрудно понять, почему заряженная частица должна быть тяжелее нейтральной. Но что можно сказать о таких парах, как нейтрон и протон, где наблюдаемая разность масс оказывается совсем другой? Эти частицы оказываются довольно сложными, и вычисление их электромагнитной массы более хитро. Например, хотя нейтрон в целом нейтрален, у него все же есть внутреннее распределение заряда и равен нулю только суммарный заряд. Мы думаем, что нейтрон, по крайней мере в некоторые моменты времени, выглядит как протон, окруженный «облаком» отрицательного π-мезона (фиг. 28.5). И несмотря на то, что нейтрон «нейтрален», т. е. полный его заряд равен нулю, у него все же есть какая-то электромагнитная энергия (например, у него есть магнитный момент), так что без детальной теории внутренней структуры судить о знаке электромагнитной разности масс нелегко.
Вас, конечно, беспокоят разные знаки разности масс в таблице. Нетрудно понять, почему заряженная частица должна быть тяжелее нейтральной. Но что можно сказать о таких парах, как нейтрон и протон, где наблюдаемая разность масс оказывается совсем другой? Эти частицы оказываются довольно сложными, и вычисление их электромагнитной массы более хитро. Например, хотя нейтрон в целом нейтрален, у него все же есть внутреннее распределение заряда и равен нулю только суммарный заряд. Мы думаем, что нейтрон, по крайней мере в некоторые моменты времени, выглядит как протон, окруженный «облаком» отрицательного π-мезона (фиг. 28.5). И несмотря на то, что нейтрон «нейтрален», т. е. полный его заряд равен нулю, у него все же есть какая-то электромагнитная энергия (например, у него есть магнитный момент), так что без детальной теории внутренней структуры судить о знаке электромагнитной разности масс нелегко.