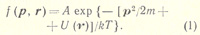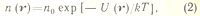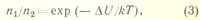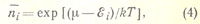Больцмана распределение

Больцмана распределение, статистически равновесная функция распределения по импульсам р и координатам r частиц идеального газа, молекулы которого движутся по законам классической механики, во внешнем потенциальном поле:

Здесь p²/2m — кинетическая энергия молекулы массой m, U(ν) — её потенциальная энергия во внешнем поле, Т — абсолютная температуpa газа. Постоянная А определяется из условия, что суммарное число частиц, находящихся в различных возможных состояниях, равно полному числу частиц в системе (условие нормировки).
Больцмана распределение представляет собой частный случай канонического распределения Гиббса для идеального газа во внешнем потенциальном поле, т. к. при отсутствии взаимодействия между частицами распределение Гиббса распадается на произведение Больцмана распределения для отдельных частиц. Больцмана распределение при U=0 даёт Максвелла распределение. Фкнкцию распределения (1) иногда называют распределением Максвелла — Больцмана, а распределением Больцмана называют функцию распределения (1), проинтегрированную по всем импульсам частиц и представляющую собой плотность числа частиц в точке ν:

где n₀— плотность числа частиц системы в отсутствии внешнего поля. Отношение плотностей числа частиц в различных точках зависит от разности значений потенциальной энергии в этих точках

где ΔU= U(ν₁)-U(ν₂). В частности, из (3) следует барометрическая формула, определяющая распределение по высоте газа в поле тяготения над земной поверхностью. В этом случае ΔU=mgh, где g — ускорение свободного падения, m — масса частицы, h — высота над земной поверхностью. Для смеси газов с различной массой частиц Больцмана распределение показывает, что распределение парциальных плотностей частиц для каждого из компонентов независимо от других компонентов. Для газа во вращающемся сосуде U (r) определяет потенциал поля центробежных сил U (r)=-mω²r²/2, где ω — угловая скорость вращения. На этом эффекте основано разделение изотопов и высокодисперсных систем при помощи ультрацентрифуги.
Для квантовых идеальных газов состояние отдельных частиц определяется не импульсами и координатами, а квантовыми уровнями энергии Ε_i частицы в поле U(r). В этом случае среднее число частиц в i-том квантовом состоянии, или среднее число заполнения, равно:

где μ — химический потенциал, определяемый из условия, что суммарное число частиц на всех квантовых уровнях Ε_i равно полному числу частиц N в системе: Σin_i=N. Формула (4) справедлива при таких температурахpax и плотностях, когда среднее расстояние между частицами значительно больше длины волны де Бройля, соответствующей средней тепловой скорости, т. е. когда можно пренебречь не только силовым взаимодействием частиц, но и их взаимным квантовомеханическим влиянием (нет квантового вырождения газа. (см. Вырожденный газ). Таким образом, Больцмана распределение есть предельный случай как Ферми — Дирака распределения, так и Бозе — Эйнштейна распределения для газов малой плотности.